F numberin alphabet

Most pho­tog­ra­phers sim­ply com­mit the stan­dard f‑number scale to mem­o­ry. How­ev­er, if you’re hav­ing trou­ble, a more straight­for­ward method is to remem­ber just the first two numbers—1 and 1.4—because the rest of the scale is an iter­a­tion of dou­bling each in alter­nat­ing order. The next f‑number is always dou­ble the pre­vi­ous one. So the num­ber after ƒ/1.4 is dou­ble of ƒ/1, which is ƒ2. Like­wise, the num­ber after ƒ/2 is dou­ble of ƒ/1.4, which is ƒ/2.8.  And on and on it goes.

We express aper­ture val­ues using f‑numbers and not as the mea­sured size of the entrance pupil, such as its diam­e­ter, radius, or area, because it neglects the essen­tial role of focal length. This can be demon­strat­ed with a thought exer­cise.

When you hold a lens up and look at the aper­ture, what you’re see­ing is tech­ni­cal­ly called the “entrance pupil.” The entrance pupil is the opti­cal image of the phys­i­cal aper­ture as seen through the front of the lens. This dis­tinc­tion mat­ters because when you look at the front of a lens, you see the aper­ture through mul­ti­ple lay­ers of glass that affect its mag­ni­fi­ca­tion and per­ceived loca­tion in space com­pared to the phys­i­cal open­ing in the iris. For the sake of sim­plic­i­ty, I’ll use “aper­ture” when refer­ring to both the set­ting and the phys­i­cal open­ing and “entrance pupil” in ref­er­ence to dimen­sions.

Let’s pre­tend we have two lens­es attached to iden­ti­cal cam­eras: one lens is 50 mm and the oth­er is 100 mm, and both have entrance pupils with 25 mm diam­e­ters. Since their entrance pupils are iden­ti­cal in size, an equal amount of light enters each lens. How­ev­er, because the focal length of the 100 mm lens is twice that of the 50 mm lens, the light pass­ing through it has to trav­el twice the dis­tance to reach its camera’s image sen­sor, which pro­duces a dark­er image.

F-stop vs aperture

The 100 mm lens can pro­vide an expo­sure equal to its 50 mm coun­ter­part by open­ing its aper­ture to col­lect four times more light, assum­ing its aper­ture can open that much. Since aper­tures are rough­ly cir­cu­lar, we can deter­mine how big they should be by cal­cu­lat­ing the area of a cir­cle. An entrance pupil with a 25 mm diam­e­ter has an area of about 491 mm^2. The 100 mm lens would need an entrance pupil with an area of 1,964 mm^2, which is formed by a cir­cle with a 50 mm diam­e­ter. Sim­ple, right?

Reduc­tion in bright­ness occurs because light has the prop­er­ty of spread­ing out as it recedes from its source, and from the per­spec­tive of your camera’s image sen­sor, this source is the point inside the lens from which focal length is mea­sured. This trait of light to dif­fuse out­wards is described by the Inverse Square Law, which states that inten­si­ty is inverse­ly pro­por­tion­al to the square of the dis­tance. In this exam­ple, the inverse square law informs us that the 100 mm lens expos­es its camera’s image sen­sor to 1/4 the light com­pared to the 50 mm lens because it’s twice as long. This occurs because one over two squared equals one-quar­ter.

What is f numbernikon

Hi there, my name is Paul, and this is Expo­sure Ther­a­py. In this video, I’ll explain the rea­son for the inverse numer­i­cal rela­tion­ship between f‑numbers and the aper­ture. This rela­tion­ship is a wide­spread point of con­fu­sion for many begin­ner pho­tog­ra­phers, who regard it as irra­tional or need­less­ly com­plex. My goal is to dis­pel the mys­tery around f‑numbers and demon­strate why they’re a per­fect­ly rea­son­able method for express­ing how the aper­ture affects expo­sure.

The best way to address this is by start­ing with the basics. Inside every inter­change­able lens is a ring of over­lap­ping blades col­lec­tive­ly known as an iris diaphragm or iris. Expand­ing or con­tract­ing the blades adjusts the open­ing in the cen­tre of the iris, called the aper­ture.

There is a huge range of colours that we can see, but simply cannot include in an object that doesn't emit light, like a painting. Think of bright neon lights.

Chang­ing the size of the aper­ture adjusts the inten­si­ty of light pass­ing through the lens. Increas­ing the aperture’s size allows more light to pass through the lens, increas­ing expo­sure and cre­at­ing a brighter pic­ture. Con­verse­ly, decreas­ing the aperture’s size reduces how much light pass­es through the lens, reduc­ing expo­sure and result­ing in a dark­er pho­to.

What is f numberin photography

I hope this helped you under­stand the inverse numer­i­cal rela­tion­ship between f‑numbers and their effect on the aper­ture. If you have requests for future top­ics, let me know in the com­ments, and I’ll address them in future videos. In the mean­time, you can learn more about pho­tog­ra­phy on ExposureTherapy.ca. See you next time.

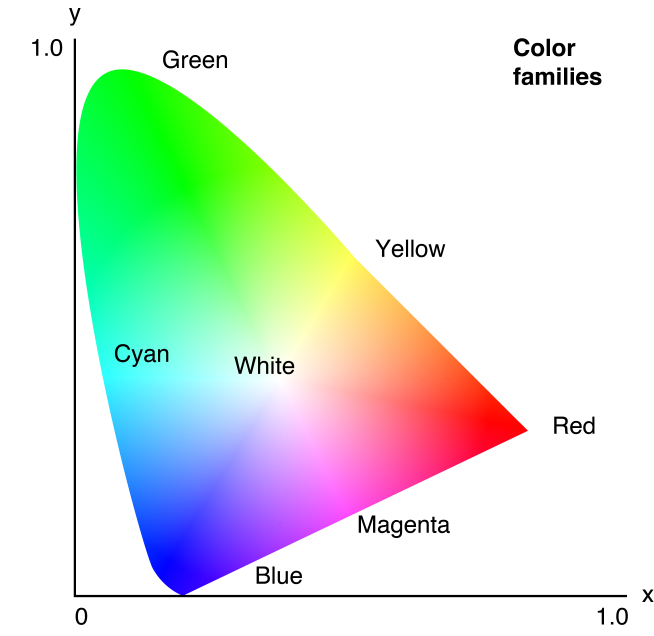
Our eyes perceive colours with sensors (optical cones) that are each sensitive to a specific range of wavelengths of light. Different species of animals have different numbers of cones, which are sensitive to different wavelengths - bees and shrimp can see colours we can't even imagine. Humans have three cone receptors, these are sensitive to three wavelengths (or colours) of light - red, green and blue.

f-number calculator

In the context of the colours we can see and have available as pigments, in a subtractive colour mixing, we cover the largest mixing area as well as the largest selection of named colours by starting with a triad of cyan, magenta and yellow. Although we see a wide range of greens, missing the brightest greens has less of an impact on our perception than missing a yellow.Will you select a cyan, magenta, yellow triad for your next palette?

Right about now you might be getting confused. First I said that cyan, magenta and yellow were primary colours. Now I'm saying that blue, green and red are the "primary" colours, the building blocks that we see all other colours from. What gives?You see, there's a difference between how we perceive coloured light (different wavelengths of light) and coloured objects. Coloured light is a specific wavelength of light (or combination of wavelengths) shining at us. Coloured objects (like watercolour on a paper), are objects that absorb some wavelengths and reflect others. A yellow object, for example, will absorb blue light, reflecting a range of light wavelengths that trigger our green and red cones.It is impossible to mix a bright yellow from any colours except other yellows (except perhaps extremely yellowish greens and oranges) in paint, because as soon as you choose a slightly different colour, you will start reflecting some blue, or stop reflecting as much green or red, resulting in a mixed colour that we perceive as something other than yellow.The "primary" colours of cyan, magenta and yellow, in the context of painting, are the colours which we see least well. There's a huge range of different wavelengths and combinations that we perceive as green, blue or red, but fewer that we perceive as cyan, magenta and yellow.

f-number formula

A 50 mm lens set to ƒ/4 will have an entrance pupil diam­e­ter of 12.5 mm—because 50 divid­ed by 12.5 equals 4. A 24 mm lens set to ƒ/8 will have an entrance pupil diam­e­ter of 3 mm. Some lens­es can open to ƒ1.0, in which case the entrance pupil diam­e­ter and focal length are equal.

This is pre­cise­ly why the f‑number is some­times called the f‑ratio. The f‑number express­es a ratio of the lens focal length to the diam­e­ter of the entrance pupil, and it’s defined by the equa­tion N=ƒ/D. Thus, the f‑number equals the focal length divid­ed by the entrance pupil diam­e­ter. It can also be mod­i­fied to solve for the entrance pupil diam­e­ter using the equa­tion D=ƒ/N. Thus, the entrance pupil diam­e­ter equals the focal length divid­ed by the f‑number.

For­tu­nate­ly, pho­tog­ra­phers don’t need to per­form such cal­cu­la­tions to take pic­tures! That’s because hid­den with­in these num­bers is a straight­for­ward rela­tion­ship. For exam­ple, notice how the expo­sure pro­duced by the 50 mm lens with a 25 mm entrance pupil is iden­ti­cal to the 100 mm lens with a 50 mm entrance pupil. This is because in both cas­es, the ratio of the focal length to the entrance pupil diam­e­ter is 2:1.

What is F numberin welding

Unfor­tu­nate­ly, the rela­tion­ship between f‑numbers, aper­ture size, and pic­ture bright­ness is not as imme­di­ate­ly intu­itive. Begin­ners are con­fused by the neg­a­tive (or inverse) rela­tion­ship between f‑numbers and aper­ture size. In addi­tion, they have a hard time under­stand­ing why big­ger f‑numbers rep­re­sent small­er aper­tures that reduce bright­ness, and small­er f‑numbers define larg­er aper­tures that increase bright­ness.

These equa­tions demon­strate that choos­ing the same f‑number on a lens of any focal length will result in the same amount of light pass­ing through the lens. They also explain the inverse rela­tion­ship between f‑numbers and expo­sure. For a giv­en focal length, as the aperture’s size increas­es, the ratio decreas­es, and vice ver­sa.

F-number of lens

The stan­dard f‑number scale is: 1, 1.4, 2, 2.8, 4, 5.6, 8, 11, 16, 22, 32, and so on. The dif­fer­ence in expo­sure between adja­cent num­bers is one stop, which means that it either dou­bles or halves the amount of light pass­ing through the lens depend­ing on whether you’re open­ing or clos­ing the aper­ture. How­ev­er, the numer­ic sequence grows by a fac­tor of about 1.4 or shrinks by a fac­tor of about 0.7.

In both cas­es, the rela­tion­ship between the set­ting and its effect on pic­ture bright­ness is easy to under­stand because there’s a pos­i­tive cor­re­la­tion, and they move in tan­dem. For exam­ple, when you dou­ble the expo­sure dura­tion, it dou­bles the bright­ness; when you halve the ISO, it halves the bright­ness. It’s a sim­ple rela­tion­ship that stu­dents in my pho­tog­ra­phy work­shops grasp with ease.

When two or more receptors both react to a light source, we see an in-between colour depending on how much each receptor reacted - for example, if we see both red and green light equally, we perceive it as yellow. If both blue and red receptors, far apart on the colour wheel, both react without triggering the green cones, we see an "imaginary" colour with no wavelength, magenta.Cyan, Magenta and Yellow are the three colours of light we see least well - narrow wavelength ranges only triggered at the outside edges where two receptors intersect.

There is an additional factor, which is that our cones are not evenly spaced across the colour spectrum. We frequently represent the range of colours that we see as colour wheels, like the colour wheels above showing the mixing range of different colour combinations. However, our visual spectrum is better represented as this wonky horseshoe shape.

I'm not a huge fan of thinking in terms of primary colours. I find it unnecessarily restrictive. After all, you can definitely mix primary colours from secondary colours. However, in my palette building series on my youtube channel, I just recommended a Cyan, Magenta, Yellow triad as your first three colours

If you want to mix a wide range of colours using few tubes of paints, some colour selections do provide a larger mixing gamut than others. Specifically, a primary triad consisting of cyan, magenta and yellow will give you the widest possible range of bright colours. What is special about these three colours?To answer this question, we need to understand how eyes work.

Last­ly, dou­bling the f‑number, such as chang­ing it from ƒ/2.8 to ƒ/5.6, reduces pic­ture bright­ness by one-quar­ter. And con­verse­ly, halv­ing the f‑number, such as adjust­ing from ƒ/8 to ƒ/4, increas­es pic­ture bright­ness four times.

Under­stand­ing the rela­tion­ship between pic­ture bright­ness and both the shut­ter speed and ISO is straight­for­ward for stu­dents learn­ing the basics of pho­tog­ra­phy. Shut­ter speed is expressed numer­i­cal­ly in time units, with the most com­mon being frac­tions of a sec­ond; longer dura­tions result in brighter pic­tures, and short­er dura­tions result in dark­er pic­tures. ISO is also expressed numer­i­cal­ly; big­ger num­bers pro­duce brighter pho­tos, and small­er num­bers make dark­er pho­tos.