Table 3 shows the performance characteristics for the overall Spot recommendation by the ARF and ARF or amblyopia (ARF+A) criteria and for each specific disease diagnosis across all patients and stratified by patient age. The overall Spot recommendation performed reasonably well in this clinic population compared to the ARF criterion and had an overall sensitivity of 0.88 and a specificity of 0.78. This performance was similar when considering the ARF+A criterion, with a sensitivity of 0.85 and specificity of 0.79. Overall Spot performance compared to the ARF or ARF+A guidelines was generally poorer in children under the age of 4 for both the ARF and ARF+A criteria. Applying updated AAPOS guidelines to the Spot measurements to assess myopia, hyperopia, anisometropia, and astigmatism generally yielded moderate to poor sensitivity but excellent specificity. Considering all age groups, sensitivities for the specific diagnoses ranged from 0.27 to 0.77 (similar results were observed when stratifying on <4 or ≥4 years of age). However, specificities were >0.9 for all four diagnoses across all children and within each age group.

Spot VisionScreener price

While conventional direct imaging can be thought as an embarrassingly parallel process that does not exploit the structure of the scene, in contrast most current CS hardware (such as the single pixel camera) require a heavily sequential process that does take into account the structure of the scene. Our approach borrows from the best of both acquisition processes, in that it is both embarrassingly parallel and takes into account the structure of the scene.

Goetschy, A. & Stone, A. D. Filtering Random Matrices: The Effect of Incomplete Channel Control in Multiple Scattering. Phys. Rev. Lett. 111, 063901 (2013).

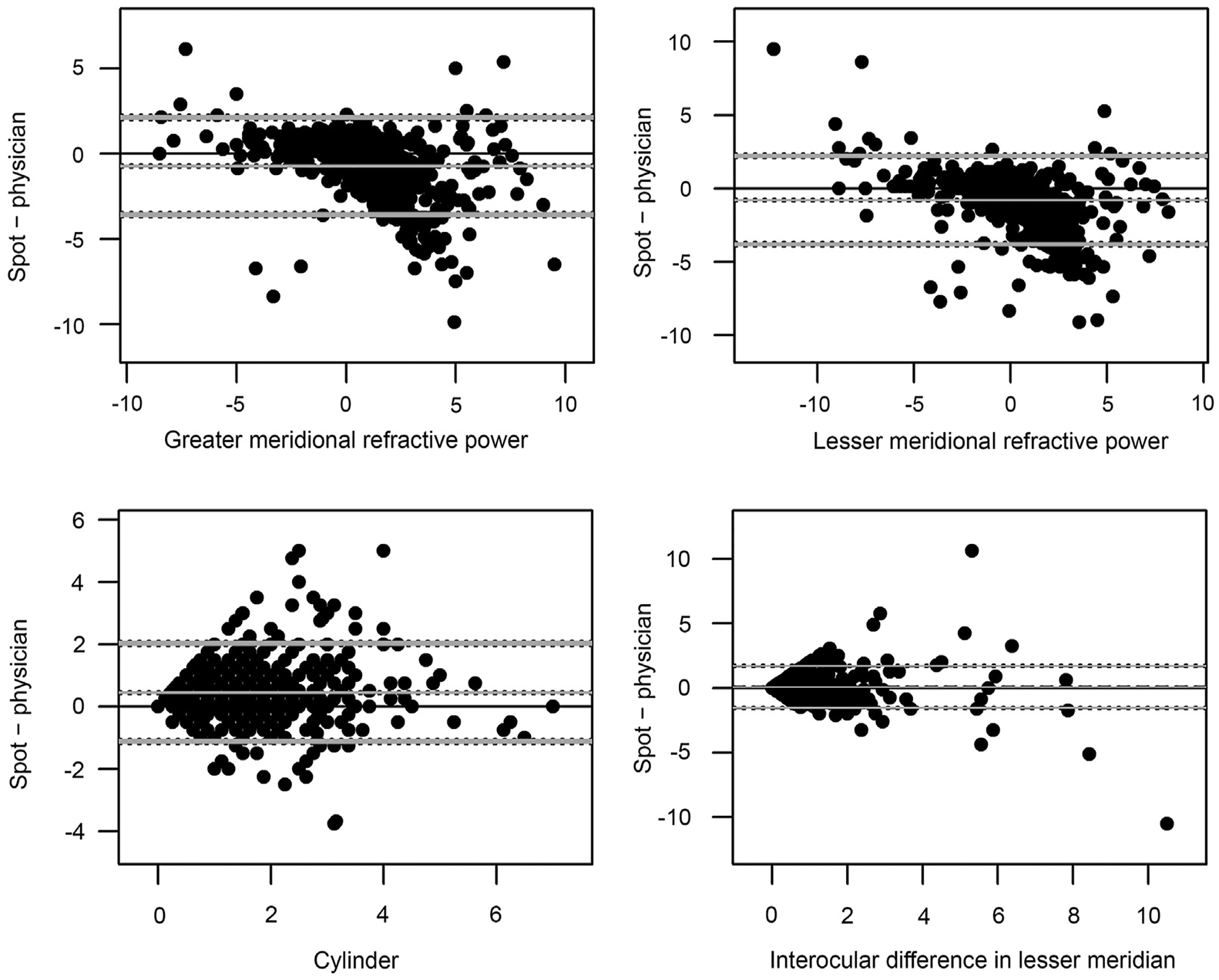
Our findings confirm again that the Spot remains poorly sensitive (0.27) in detecting hyperopia.19,23–25 Bland-Altman curves (Figure 1) demonstrate a tendency toward underestimation of hyperopia by the Spot screener, increasing with higher levels of hyperopia. Most outliers on the Bland-Altman plots are children with underestimated hyperopia. It is likely that accommodation on the Spot device plays a role in this finding. While there is a correlation between uncorrected hyperopia and poor academic performance, the causative effect of uncorrected hyperopia on learning and academic achievement is not well established.26–28 It is not known to what degree underestimation of hyperopia affects the ability of the Spot to identify children having or at risk of developing accommodative esotropia.

The Spot Vision Screener (Welch Allyn, Skaneateles Falls, NY) is marketed and has been validated as a tool to detect ARF using previous guidelines.4,12,15–19 We sought to further determine the accuracy of the Spot in our population of pediatric ophthalmology patients using the updated AAPOS 2021 guidelines and suggest device settings to maximize efficacy using these updated expert consensus guidelines.20

Table 4A shows manufacturer refractive criteria for Spot screener, version 2.0.16. To identify Spot criteria that optimize sensitivity and specificity for the different diagnoses, we examined different cutoff values for the Spot measurements and evaluated their effect on sensitivity and specificity for each diagnosis. Table 4B shows the cutoff values for the Spot that provide the optimal sensitivity and specificity for myopia, hyperopia, anisometropia, and astigmatism. The optimal cutoff was selected as the cutoff that yielded the largest product of sensitivity and specificity and/or for which both sensitivity and specificity were >0.8. A majority of cutoffs provide both sensitivity and specificity >0.8, the only exceptions being the cutoffs for astigmatism in children <4 years of age (sensitivity = 0.88, specificity = 0.66) and hyperopia in children ≥4 years (sensitivity = 0.77, specificity = 0.82).

The performance of the proposed compressive sampler for all sampling and sparsity rates of interest is summarized on Fig. 5, which is the main result of this paper. It gives the probability of successful reconstruction displayed as a function of the sensor density M/N and relative sparsity k/M. Each point of this surface is the average reconstruction performance for real measurements over approximately 50 independent trials. As can be seen, this experimental diagram exhibits a clear “phase transition” from complete failure to systematic success. This thorough experimental study largely confirms that the proposed methodology for sampling using scattering media indeed reaches very competitive sampling rates that are far below the Shannon-Nyquist traditional scheme.

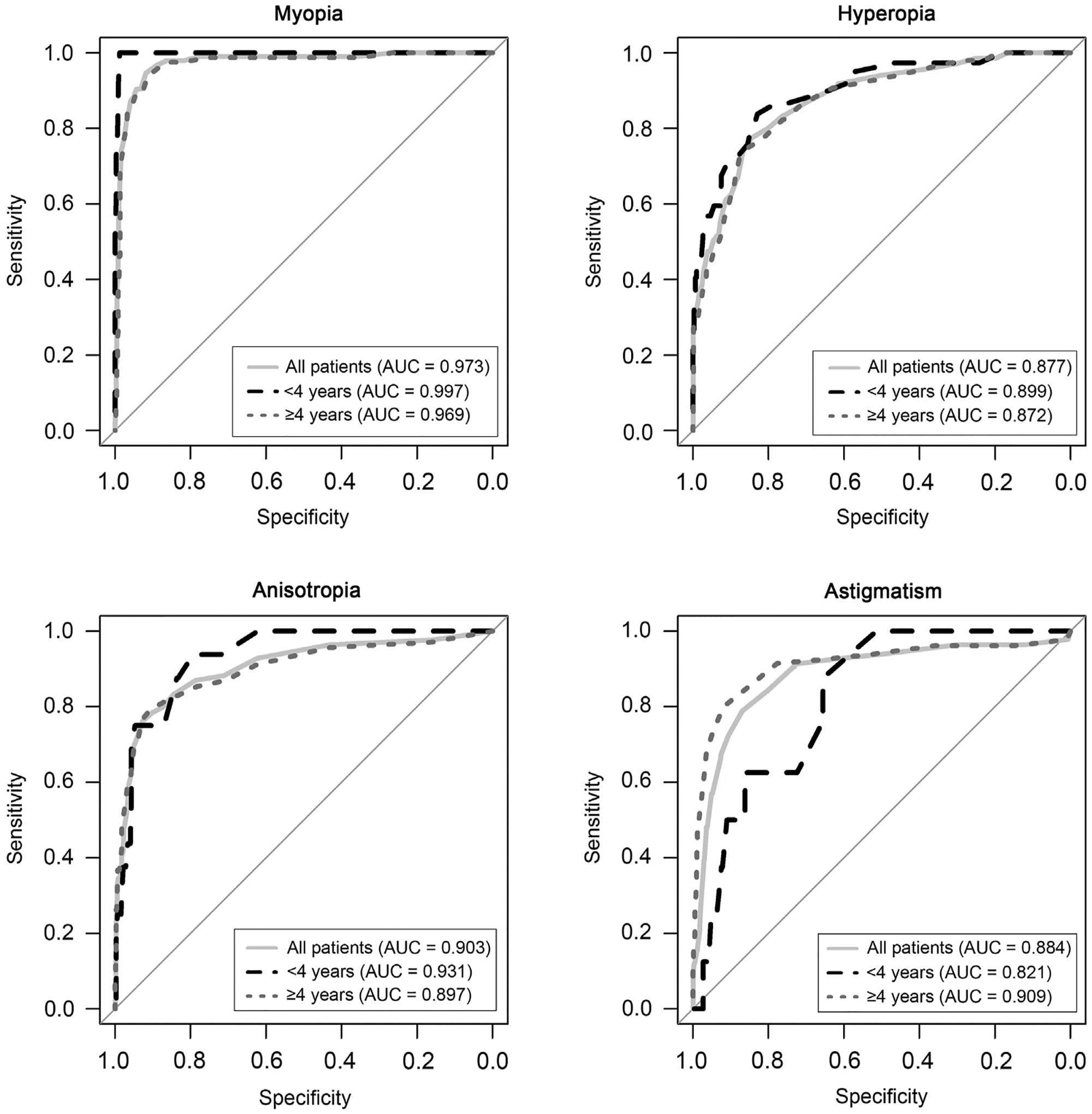
The ROC curves for the appropriate Spot parameter for each diagnosis (hyperopia, myopia, astigmatism, and aniso-metropia) across all patients and stratified by patient age (<4 or ≥4 years) are shown in Figure 2. The AUC for the different diagnoses ranged from 0.88 to 0.97 across all children, from 0.82 to 0.99 when only children <4 years of age were considered and from 0.87 to 0.97 in children ≥4 years of age. The AUCs for myopia were larger than for the other three diagnoses and were similar between age groups. The AUCs for hyperopia, anisometropia, and astigmatism were similar (between 0.88 and 0.90 across all children) and were generally similar for older and younger children.

Experimental probability of successful recovery (between 0 and 1) for a k-sparse image of N pixels via M measurements. On the x-axis is displayed the sensor density ratio M/N. A ratio of 1 corresponds to the Nyquist rate, meaning that all correct reconstructions found in this figure beat traditional sampling. On the y-axis is displayed the relative sparsity ratio k/M. A clear phase transition between failure and success is observable, which is close to that obtained by simulations (dashed line), where exactly the same experimental protocol was conducted with simulated noisy observations both for calibration and imaging. Boxes A, B, C and D locate the corresponding examples of Fig. 4. Each point in this 50 × 50 grid is the average performance over approximately 50 independent measurements. This figure hence summarizes the results of more than 105 actual physical experiments.

(a) Classical Nyquist-Shannon sampling, where the waves originating from the object, of size N, are captured by a dense array of M = N sensors. (b) The “Single Pixel Camera” concept, where the object is sampled by M successive random projections onto a single sensor using a digital multiplexer. (c) Imaging with a multiply scattering medium. The M sensors capture, in a parallel fashion, several random projections of the original object. In cases (b) and (c), sparse objects can be acquired with a low sensor density M/N < 1.

Examples of actual reconstructions performed by our analog compressive sampler are shown on Fig. 4. As can be seen, near-perfect reconstruction of complex sparse patterns occur with sensor density ratios M/N that are much smaller than in classical Shannon-Nyquist sampling (M = N). An important feature of the approach is its universality: reconstruction is also efficient for objects that are sparse in the Fourier domain.

Welch AllynSpot Vision

Reconstruction of the sparse objects was then achieved numerically using the M × P measurements only. The TM used for reconstruction is the one estimated in the calibration phase. In order to demonstrate the efficiency and the simplicity of the proposed system, we used the simple Multichannel Orthogonal Matching Pursuit algorithm42 for MMV reconstruction. It should be noted that more specialized algorithms may lead to better performance and should be considered in the future.

Correspondence: M. Millicent Peterseim, MD, Storm Eye Institute, Department of Ophthalmology, Medical University of South Carolina, 167 Ashley Ave., Charleston, SC 29425 (petersem@musc.edu).

Yin, W. & Zhang, Y. Extracting salient features from less data via l1-minimization. SIAG/OPT Views-and-News 19, 11–19 (2008).

We provide recommendations for Spot cut-off referral criteria to maximize sensitivity and specificity for the updated 2021 AAPOS guidelines. The out-of-the-box Spot manufacturer criteria can be adjusted by the user for desired sensitivity and specificity. Results of our study suggest increasing the instrument referral criterion for astigmatism from 1.5 D (manufacturer thresholds of the screener used in this study) to 2 D in older children.16–17 An additional recommendation would decrease the anisometropia cut-off from 1 D to 0.75 D, which improves sensitivity from 0.59 to >0.8. The manufacturer may wish to consider these recommendations in future out-of-the box software versions.

In practice, when trying to implement Compressive Sensing in a hardware device, fulfilling this incoherence requirement is nontrivial. It requires a way to deterministically scramble the information somewhere between the object and the sensors. Theory shows that an efficient way to do this is by using random measurement matrices H or HB2,3,4. Using such matrices, it can indeed be shown26 that the number of samples required to recover the object is mostly governed by its sparsity k, i.e. the number of its nonzero coefficients in the given basis. If the coefficients of the M × N measurement matrix are independent and identically distributed (i.i.d.) with respect to a Gaussian distribution, perfect reconstruction can be achieved with only measurements27. Furthermore, many algorithms are available, for instance Orthogonal Matching Pursuit (OMP) or Lasso26,28, which can efficiently perform such reconstruction under sparsity constraints.

As can be seen, each of the M measurements of the output complex field may hence be considered as a scalar product between the input and the corresponding row of the TM. If multiply scattering materials have already been considered for the purpose of focusing, thus serving as perfect “opaque lenses”17,18, the main idea of the present study is to exploit them for compressive imaging. In other wavelength domains than optics, analogous configurations may be designed to achieve CS through multiple scattering. For instance, a collection of randomly packed metallic scatterers could be used as a multiply scattering media from the microwave domain up to the far infrared and the method proposed here could allow imaging at these frequencies with only a few sensors. A similar approach could be used to lower the number of sensors in 3D ultrasound imaging using CS through multiple scattering media.

Cotter, S. F. Sparse solutions to linear inverse problems with multiple measurement vectors. IEEE T. Signal Process 53, 2477–2488 (2005).

Cohen, A., Dahmen, W. & DeVore, R. Compressed sensing and best k-term approximation. J. Am. Math. Soc. 22, 211–231 (2009).

Compressive sampling with multiply scattering material has several advantages. First, it has recently been shown that they have an optimal multiplexing power for coherent waves22, which consequently makes them optimal sensors within the CS paradigm. Second, these materials are often readily available and require very few engineering. In the domain of optics for example, we demonstrate one successful implementation using a 300 μm layer of Zinc Oxide (ZnO), which is essentially white paint. Third, contrarily to most aforementioned approaches, this sensing method provides the somewhat unique ability to take a scalable number of measurements in parallel, thus with a potential of strongly reducing acquisition time. In practice, if 500 samples are required to reconstruct a given image using CS principles, this imaging framework allows their acquisition at once on 500 independent sensors, whereas state-of-the-art systems such as the single pixel camera require a sequence of 500 random patterns on the DMD.

Patients were considered to have ARFs or VSREs (henceforth, “ARFs”) based on the comprehensive examination and the physician’s diagnosis and 2021 AAPOS ARF guidelines (Table 1). Sensitivity, specificity, and positive and negative predictive values (PPV and NPV) of the Spot in detecting ARF were calculated. Children in whom the Spot was unable to obtain a result were included as automatic referrals. An additional analysis was carried out to include children with a diagnosis of amblyopia as a risk factor (“ARF+A”).

The difference between physician- and Spot-reported measures for each parameter are shown in the Bland-Altman plots in Figure 1. Points on the Bland-Altman plots represent the difference between the Spot and physician measures versus the mean of the two measures for each patient for the following: maximum meridional refractive power, minimum meridional refractive power, cylinder, and anisometropia (defined as the interocular difference in the lesser meridian). Maximum and minimum meridional powers both showed an overall negative bias (middle gray line below 0) toward lower values for the Spot screener, with greater underestimation of meridional power at higher levels of hyperopia. A small positive overestimation of astigmatism by the Spot is present compared with the physician measure. With regard to outliers on these plots, 89 of 1090 participants (8.2%) for whom the Spot could evaluate sphere had a Spot screener greater or lesser sphere that underestimated the physician lesser or greater meridional value by 3.5 D or more (less hyperopic, or more myopic), and a majority of these subjects were highly hyperopic. Fewer than 1% of participants (9 of 1,090) had a Spot screener greater or lesser sphere that overestimated the physician lesser or greater meridional value by ≥3.5 D (more hyperopic, or less myopic), and 6 of these subjects were highly myopic.

Popoff, S. M. et al. Measuring the transmission matrix in optics: an approach to the study and control of light propagation in disordered media. Phys. Rev. Lett. 104, 100601 (2010).

On practical grounds, the use of a multiply scattering material in CS raises several ideas that we consider in this study. First, the random multiplexing achieved through multiple scattering must be measured a posteriori, since it is no longer known a priori as in engineered random sensing. This calibration problem has been the topic of recent studies in the context of CS23 and we propose here a simple least squares calibration procedure that extends our previous work24,25. Second, the use of such a measured Transmission Matrix (TM) induces an inherent uncertainty in the sensing mechanism, that can be modeled as noise in the observations. As we show both through extensive simulations and actual experiments, this uncertainty is largely compensated by the use of adequate reconstruction techniques. In effect, the imager we propose almost matches the performance of idealized sub-Nyquist random sensing.

Elad, M. Sparse and redundant representations: from theory to applications in signal and image processing. (Springer, 2010).

Examples of signals, which are sparse either in the Fourier or canonical domain (left), along with their actual experimental reconstruction using a varying number of measurements. (a) Fourier-sparse object (b–c) canonical sparse objects. In (b), small squares are the original object and large squares are the reconstruction. In all cases, the original object contains 1024 pixels and is thus sampled with a number M of sensors much smaller than N. A, B, C and D images are correspondingly represented in the phase transition diagram of Fig. 5.

Candès, E. J. et al. Compressed sensing with coherent and redundant dictionaries. Appl. Comput. Harmon. A. 31, 59–73 (2011).

This study was approved by the Medical University of South Carolina Institutional Review Board and complied with the US Health Insurance Portability and Accountability Act of 1996. Informed consent was obtained from the patients’ guardians prior to enrollment. The protocol of this continuing prospective study has been previously reported.21–23 This analysis included patients age 6 months to 13 years presenting for complete pediatric ophthalmological examination when study personnel were available between June 2013 and August 2021. The Spot software v.2.1.4 with installed manufacturer out-of-the-box cut-offs were used. Children were screened with the Spot Vision Screener by lay personnel prior to examination.

Candès, E. J. Compressive sampling. Proceedings of the International Congress of Mathematicians: Madrid, August 22–30, 2006: invited lectures. 2006.

FailedSpot visiontest

Within the imaging device, waves coming from the object (i) go through a scattering material (ii) that efficiently multiplexes the information to all M sensors (iii). Provided the transmission matrix of the material has been estimated beforehand, reconstruction can be performed using only a limited number of sensors, potentially much lower than without the scattering material. In our optical scenario, the light coming from the object is displayed using a spatial light modulator.

In our study population, the overall predictive ability of the Spot is good, with a sensitivity of 0.88 and a specificity of 0.78. We recommend specific device refractive referral criteria to maximize screening effectiveness using the updated AAPOS guidelines.

For a TM to be efficient in a CS setup, it has to correctly scramble the information from all of its inputs to each of its outputs. It is known that a matrix with i.i.d Gaussian entries is an excellent candidate for CS31 and the TM of optical multiple scattering materials were recently shown to be well approximated by such matrices22. The rationale for this fact is that the transmission of light through an opaque lens leads to a very large number of independent scattering events. Even if the total transmission matrix that links the whole input field to the transmitted field shows some non-trivial mesoscopic correlations32, recent studies proved that these correlations vanish when controlling/measuring only a random partition of input/output channels22. In our experimental setup, the number of sensors is very small compared to the total number of output speckle grains and we can hence safely disregard any mesoscopic correlation.

Ohlsson, H. et al. Compressive phase retrieval from squared output measurements via semidefinite programming. arXiv, 1111.6323 (2011).

In its simplest form, CS may be understood as a way to solve an underdetermined linear inverse problem. Let x be the object to image, understood as a N × 1 vector and let us suppose that x is only observed through its multiplication y by a known measurement matrix H, of dimension M × N, we have y = Hx. Each one of the M entries of y is thus the scalar product of the object with the corresponding row of H. When there are fewer measurements than the size of the object, i.e. M < N, it is impossible to recover x perfectly without further assumptions, since the problem has infinitely many solutions. However, if x is known to be sparse, meaning that only a few of its coefficients are nonzero (such as stars in astronomical images) and provided H is sufficiently random, x can still be recovered uniquely through sparse optimization techniques1.

The 2021 AAPOS guidelines update is designed to increase sensitivity for anisometropia in younger children while reducing false-positive referrals in preschoolers, especially those due to symmetric, moderate astigmatism. An additional goal is to detect lower magnitudes of astigmatism and myopia in older children as these conditions may influence school performance and be amenable to myopia prevention therapy. Our analysis suggests that the guidelines update will prove effective toward these goals.

The AUC analysis of ROC curves (Figure 2) demonstrates overall good prediction performance for the Spot parameter for each diagnosis (range, 0.88 to 0.97). The second highest predictive performance is that for anisometropia in younger children (AUC > 0.93), for whom therapy to treat or even prevent amblyopia is most effective. The highest predictive performance is that for myopia for all children (AUC > 0.97), for which therapy exists to reduce myopic progression.

Our approach is summarized in Fig. 1(c) and its implementation in an optical experiment is depicted in Fig. 2. The coherent waves originating from the object and entering the imaging system propagate through a multiply scattering medium. Within the imager, propagation produces a seemingly random and wavelength-dependent interference pattern called speckle on the sensors plane. The speckle figure is the result of the random phase variations imposed on the waves by the propagation within the multiply scattering sample29. Scattering, although the realization of a random process, is deterministic: for a given input and as long as the medium is stable, the interference speckle figure is fully determined and remains constant. In essence, the complex medium acts as a highly efficient analog multiplexer for light, with an input-output response characterized by its transmission-matrix24,25. We highlight the fact that the multiple scattering material is not understood here as a nuisance occurring between the object and the sensors, but rather as a desirable component of the imaging system itself. After propagation, sensing takes place using a limited number M < N of sensors.

After calibration, the scattering medium can be used to perform CS, using this estimated TM as a measurement matrix. Note that, in our experiment, the same SLM used for calibration is then used as a display to generate the sparse objects. This approach is not restrictive as any sparse optical field or other device capable of modulating light could equivalently be used at this stage. As demonstrated in our results section, using such an estimated TM instead of a perfectly controlled one does yield very good results all the same, while bringing important advantages such as ease of implementation and acquisition speed. Hence, even if the proposed methodology does require the introduction of a supplementary calibration step, this step comes at the cost of a few mandatory supplementary calibration measurements rather than at the cost of performance. This claim is further developed in our results and methods sections.

Our study is limited by the fact that our population of ophthalmology patients have a relatively high disease prevalence, which may affect results, including testability. Although sensitivity and specificity estimates for individual refractive criteria should not vary according to disease prevalence in the population studied, the same is not true of a composite outcome such as “any ARF or VSRE,” for which sensitivity and specificity estimates may vary in different populations depending on the relative prevalence of the different components of the composite outcome. In addition, PPV and NPV do vary with disease prevalence, even for individual refractive criteria; to address this we also estimated PPV and NPV for the composite outcome for the general population based on published estimates of ARF or VSRE prevalence. Our estimates for the general population indicate that the PPV is reasonable at 0.55, so that 55% of children referred would be found to have a 2021 ARF or VSRE. Conversely, only 4% of children with a 2021 ARF or VSRE would be “missed” by the Spot screener. Although these estimates are useful, results from an ophthalmology office population may not correlate with results of community or school screening. We also included children up to the age of 13, and we found slightly lower sensitivity and specificity for composite outcomes in children <4 years of age compared to overall and much lower sensitivity for targeted levels of astigmatism in this subgroup than overall.

Donoho, D. & Tanner, J. Observed universality of phase transitions in high-dimensional geometry, with implications for modern data analysis and signal processing. Philos. T Roy. S. A 367, 4273–4293 (2009).

Liutkus, A., Martina, D., Popoff, S. et al. Imaging With Nature: Compressive Imaging Using a Multiply Scattering Medium. Sci Rep 4, 5552 (2014). https://doi.org/10.1038/srep05552

The newer guidelines raise the recommended gold standard target for astigmatism detection from >2 D to >3 D for children <4 years old, and from >1.50 D to >1.75 in children ≥4 years of age. The Spot has been reported to overestimate astigmatism,25 and our analysis of Bland-Altman curves comparing astigmatism measurements of the Spot and the examiner confirms a positive bias, suggesting a small overestimation of astigmatism. Within our population, the overall specificity for astigmatism is excellent at 0.93 while maintaining a good sensitivity for astigmatism (0.80) for children ≥4 years of age. The high specificity for astigmatism may reduce referrals for moderate symmetric astigmatism; the new guidelines still allow detection of significant astigmatism in children of school age.

where the mixing factor corresponds to the overall contribution of the input field xn into the output field ym. All these factors can be gathered into a complex matrix [H]mn = hmn called the Transmission Matrix (TM), which characterizes the action of the scattering material on the propagating waves between input and output. The medium hence produces a very complex but deterministic mixing of the input to the output, that can be understood as spatial multiplexing. This linear model, in the ideal noiseless case, can be written more concisely as:

This work was supported by the European Research Council (Grant N°278025), the Emergence(s) program from the City of Paris and LABEX WIFI (Laboratory of Excellence within the French Program “Investments for the Future”) under references ANR-10-LABX-24 and ANR-10-IDEX-0001-02 PSL*. G.C. is supported by the Austrian Science Fund (FWF) START-project FLAME (Y 551-N13). O.K. is supported by the Marie Curie intra-European fellowship for career development (IEF) and the Rothschild fellowship. I.C. would like to thank the Physics arXiv Blog for drawing his attention to opaque lenses and Ms. Iris Carron for her typesetting support.

Results from 1,090 children were analyzed (47.7% males; average age, 5.5 years; range, 6 months to 13 years). Patient characteristics are presented in Table 2. Spot screening was successful in 1,036 children (95%). Of the total, 369 children were <4 years of age, of whom 342 (93%) had a successful Spot screening. Forty-eight percent of participants were recommended for further examination based on Spot manufacturer guidelines, and 40% of children were found to have an ARF by gold standard examination according to the 2021 guidelines. Patient characteristics are reported in Table 2. With a prevalence of ARFs of 24%, the PPV and NPV were estimated to be 0.55 and 0.96.

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

High sensitivity for myopia is desirable in older children, for whom distance vision is important in the classroom. Using the new guidelines, the Spot demonstrates good sensitivity for myopia (0.89) in older children, with high predictive performance (AUC > 0.97).

Tropp, J. A. & Gilbert, A. C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE T. Inf. Theory 53, 4655–4666 (2007).

In the past few years, several hardware implementations capable of performing such random compressive sampling were introduced5,6,7,8,9,10,11,12,13. In optics, these include the single pixel camera6, which is depicted in Fig. 1(b) and uses a digital array of micromirrors (abbreviated DMD) to sequentially reflect different random portions of the object onto a single photodetector. Other approaches include phase modulation with a spatial light modulator10, or a rotating optical diffuser13. The idea of random multiplexing for imaging has also been considered in other domains of wave propagation. CS holds much promise in areas where detectors are rather complicated and expensive such as the THz or far infrared. In this regards, there have been proposals to implement CS imaging procedures in the THz using random pre-fabricated masks5, DMD or SLM photo-generated contrast masks on semi-conductors slabs14 and efforts are also pursued on tunable metamaterial reflectors15. Recently, a carefully engineered metamaterial aperture was used to generate complex RF beams at different frequencies8.

Thresholds refer to meridional refractive power for hyperopia and myopia and the difference in the less hyperopic meridian for anisometropia.

As in any hardware implementation of CS, experimental noise is an important issue limiting the performance, especially since it impacts the measurement matrix. Using baseline sparse reconstruction algorithms along with standard least-squares calibration techniques, we demonstrated that successful reconstruction exhibits a clear phase transition between failure and success even at very competitive sampling rates. The proposed methodology can be considered to be a truly analog compressive sampler and as such, benefits from both theoretical elegance and ease of implementation.

Gribonval, R. et al. Atoms of all channels, unite! Average case analysis of multi-channel sparse recovery using greedy algorithms. J. Four. Anal. Appl. 14, 655–687 (2008).

Spot VisionScreener How does it work

Eldar, Y. & Rauhut, H. Average case analysis of multichannel sparse recovery using convex relaxation. IEEE T. inform. Theory 56, 505–519 (2010).

Chan, W. L. et al. A single-pixel terahertz imaging system based on compressed sensing. Appl. Phys. Lett. 93, 12105 (2008).

In this study, we have demonstrated that a simple natural layer of multiply scattering material can be used to successfully perform compressive sensing. The compressive imager relies on scattering theory to optimally dispatch information from the object to all measurement sensors, shifting the complexity of devising CS hardware from the design, fabrication and electronic control to a simple calibration procedure.

During a first calibration phase, which lasts a few minutes and needs to be performed only once, a series of controlled inputs x are emitted and the corresponding outputs y are measured. The TM can be estimated through a simple least-squares error procedure, which generalizes the method proposed in24,25, as detailed in the supplementary material below. In short, this calibration procedure benefits from an arbitrarily high number of measurements for calibration, which permits to better estimate the TM. It is important to note here that the need for calibration is the main disadvantage of this technique, compared to the more classical CS imagers based on pseudo-random projections, which have direct control on the TM. However, this calibration step here involves only standard least-squares estimation of the linear mapping between input and output of the scattering material24,25. In our experimental setup, the whole calibration is performed in less than 1 minute. While we here rely on optical holography to extract complex amplitude from intensity measurements, the TM measurement can be implemented in a simplified way for other types of waves (RF, acoustics, Terahertz), where direct access to the field amplitude is possible. It may not be so straightforward in practical situations when only the intensity of the output is available and where more sophisticated methods30 would be required.

Instrument-based pediatric vision screening is endorsed by the American Academy of Pediatrics as a valid vision screening method. It allows detection of amblyopia risk factors (ARFs) at an age when amblyopia can be prevented and effectively treated.1–5 Since previous AAPOS guidelines for detection of ARFs were published in 2003 and 2013, screening devices have improved, and the prevalence and severity of risk factors has been better defined.6 In 2021, the Vision Screening Committee of the American Association for Pediatric Ophthalmology and Strabismus (AAPOS) updated guidelines for the detection of ARFs as well as visually significant refractive errors (VSREs).7 The updated “Uniform Guidelines” are used to evaluate screener effectiveness and to provide recommendations for device calibration to maximize efficacy in detecting children at risk of visual impairment.

To evaluate the Spot Vision Screener according to updated 2021 AAPOS Vision Screening Committee guidelines for instrument-based pediatric vision screen validation.

In a signal processing framework, the notion of structure may also be embodied as sparsity in a known representation1. For example, most natural images are not sparse, yet often yield near-sparse representations in the wavelet domain. If the object x is known to have some sparse or near-sparse representation s in a known basis B (x = Bs), then it may again be possible to recover it from a few samples, by solving y = HBs, provided H and B obey some technical conditions such as incoherence1,2,3,4,26.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

In this work, we replace such man-made emulated randomization by a natural multiply scattering material, as depicted in Fig. 1(c). Whereas scattering is usually seen as a time-varying nuisance, for instance when imaging through turbid media16, the recent results of wave control in stable complex material have largely demonstrated that it could also be exploited, for example so as to build focusing systems that beat their coherent counterparts in terms of resolution17,18. Such complex and stable materials are readily available in several frequency ranges -they were even coined in as one-way physical functions for hardware cryptography19. In the context of CS, such materials perform an efficient randomized multiplexing of the object into several sensors and hence appear as analog randomizers. The approach is applicable in a broad wavelength range and in many domains of wave propagation where scattering media are available. As such, this study is close in spirit to earlier approaches such as the random reference structure20, the random lens imager7, the metamaterial imager8, or the CS filters proposed in21 for microwave imaging. They all abandoned digitally controlled multiplexors as randomizers. Still, we go further in this direction and even drop the need for a designer to craft the randomizer.

Because PPV and NPV are affected by the high disease prevalence of our study population, these values were estimated for the general population. Because the frequency of ARFs is reported by cycloplegic retinoscopy as 24% in normal preschool children, this prevalence value is used to estimate PPV and NPV in the general pediatric population.24

Further evaluation with recommendations from diverse and age-appropriate community screening populations will continue to improve efficacy of pediatric instrument-based vision.19,24,29 We analyzed a large patient cohort to better define effectiveness and maximize referral criteria for the Spot vision screener.

Spot VisionScreener accuracy

Wang, J. & Shim, B. A Simple Proof of the Mutual Incoherence Condition for Orthogonal Matching Pursuit. arXiv, 1105.4408 (2011).

Receiver operating characteristics (ROC) curves for the Spot criterion for physician diagnosed myopia, hyperopia, anisometropia, and astigmatism. The three ROC curves in each panel represent the ROC across all patients (light gray solid line), in children under 4 years of age (black dashed line), and in children 4 years or older (dotted-gray line).

The Spot provides a report of pupillary diameter, ocular alignment, estimated binocular refraction, and referral recommendation—“all measurements within range” or “complete eye exam recommended.” Several attempts were made to obtain a successful reading. The Spot refractive measurement range is ±7.50 D. Patients who could not be screened (ie, no refraction estimate or recommendation) were included in this study as automatic referrals. A comprehensive examination was performed by a pediatric ophthalmologist masked to the screener results. In all patients, visual acuity, stereopsis, ocular motility, and ocular alignment were assessed, and the anterior segment was examined. Patients underwent cycloplegic refraction and a fundus examination 30–40 minutes after instillation of one drop of proparacaine hydrochloride ophthalmic solution USP 0.5% followed by 1–2 drops of tropicamide 1%/phenylephrine 2.5%/cyclopentolate 1%. Patient age and demographics were collected. The following data were collected from the Spot: whether the screening was successfully completed, estimated refraction, and referral recommendation. From the physician examination, the following data were collected: ocular motility, ocular alignment, cycloplegic refraction, diagnosis of amblyopia with history of treatment, and presence of systemic or ocular pathology.

The association between Spot recommended screening and meeting one or more ARF/ARF+A diagnosis was determined. The prediction performance for the Spot parameter used to predict each diagnosis (myopia, hyperopia, astigmatism, anisometropia) was estimated using the area under the curve (AUC) of receiver operating characteristics (ROC). All models were developed using refractive data from all patients for whom Spot screening was successful, divided into data from children less than 4 years of age, and data from children 4 years of age and older. In addition to the area under the ROC, we also calculated model sensitivity, specificity, PPV, and NPV for each outcome, determined by comparing the predicted disease status to the observed disease status. Confidence intervals for all performance parameters were calculated using the exact binomial confidence interval approach. Additionally, we examined different choices of cutoffs for Spot parameters to identify the optimal parameters to discriminate the different diagnoses. All analyses were conducted in R v. 4.1.0 (https://www.R-project.org/).

Supported in part by the South Carolina Clinical & Translational Research Institute, Medical University of South Carolina’s CTSA, NIH/NCATS Grant Number 1UL1TR001450 (BW).

Laboratoire Kastler-Brossel, UMR8552 CNRS, Ecole Normale Supérieure, Univ. Paris 6, Collège de, 24 rue Lhomond, PARIS, 75005, France

Cutoff values in diopters for the Spot that provide the optimal sensitivity and specificity for meridional myopia, meridional hyperopia, anisometropia in the lesser meridian, and astigmatism

Katz, O. et al. Non-invasive real-time imaging through scattering layers and around corners via speckle correlations. arXiv, 1403.3316 (2014).

Bland-Altman plots comparing Spot measurements to physician-reported measurements. The x-axis represents the mean of the Spot and physician measures for each child; the y-axis, the difference between the Spot and physician measures. The gray middle line represents the mean difference between the Spot and physician measures; the bottom and top gray lines represent the 95% agreement interval, that is the interval within which 95% of the differences between the first and second method fall.

During our experiments, we measured the reconstruction performance of the imaging system, when the image to reconstruct is composed of N = 32 × 32 = 1024 pixels, using a varying number M of measurements. In practice, we use a CCD array, out of which we select M pixels. These are chosen at random in the array, with an exclusion distance equal to the coherence length of the speckle, in order to ensure uncorrelated measurements. Details of the experiments can be found in the methods section below. For each sparsity level k between 1 and N, a sparse object with only k nonzero coefficients was displayed under P = 3 different random phase illuminations [Since our SLM can only do phase modulation, we used a simple trick as in41 to simulate actual amplitude objects, based on two phase-modulated measurements. See the supplementary material on this point.]. These virtual measurements may, without loss of generality, be replaced by the use of an amplitude light modulator and are anyways replaced by the actual object to image in a real use-case. The corresponding outputs were then measured and fed into a Multiple Measurement Vector (MMV) sparse recovery algorithm20. For each sparsity level, 32 such independent experiments were performed.

For CS to be efficient, the sampling must fulfill specific technical conditions that are hard to translate into practical design guidelines. In this respect, the most interesting argument featured very early on in2,3,4 is that a randomized sensing mechanism yields perfect reconstruction with high probability. As a matter of convenience, hardware designers have created physical systems that emulate this property. This way, each measurement gathers information from all parts of the object, in a controlled but pseudo-random fashion. Once this is achieved, CS theory provides good reconstruction guarantees.

NPV, negative predictive value; PPV, positive predictive value; A, amblyopia; ARF, amblyopia risk factor or visually significant refractive error as defined in Table 1.

However, these CS implementations come with some limitations. First, these devices include carefully engineered hardware designed to achieve randomization, via a DMD6, a metamaterial8 or a coded aperture11. Second, the acquisition time of most implementations can be large because they require the sequential generation of a large number of random patterns.

ARFs are stratified by amblyopia severity; combined cases could be listed by the more severe condition. Media opacity, manifest strabismus, anisometropia, and hyperopia are for all age levels. Reporting validation for each ARF and refractive error independently and also combined is recommended.

In our optical experimental setup, we used a Spatial Light Modulator (an array of N = 1024 micromirrors, abbreviated as SLM) to calibrate the system and also to display various objects, using a monochromatic continuous wave laser as light source.

The recent theory of compressive sensing leverages upon the structure of signals to acquire them with much fewer measurements than was previously thought necessary and certainly well below the traditional Nyquist-Shannon sampling rate. However, most implementations developed to take advantage of this framework revolve around controlling the measurements with carefully engineered material or acquisition sequences. Instead, we use the natural randomness of wave propagation through multiply scattering media as an optimal and instantaneous compressive imaging mechanism. Waves reflected from an object are detected after propagation through a well-characterized complex medium. Each local measurement thus contains global information about the object, yielding a purely analog compressive sensing method. We experimentally demonstrate the effectiveness of the proposed approach for optical imaging by using a 300-micrometer thick layer of white paint as the compressive imaging device. Scattering media are thus promising candidates for designing efficient and compact compressive imagers.

L.D., S.G., I.C. proposed the use of a multiply scattering material for compressive sensing. S.P., G.L. and S.G. designed the initial experimental setup. G.C. performed initial numerical analysis. D.M., O.K. and S.G. discussed the experimental implementation. D.M. and A.L. performed the experiments and A.L. performed the numerical analysis with the help of L.D. All authors contributed to discussing the results and writing the manuscript.

Gribonval, R., Chardon, G. & Daudet, L. Blind calibration for compressed sensing by convex optimization. Int. Conf. Acoust. Spee. 2713–2716 (2012).

The phase transition observed on Fig. 5 appears to be slightly different from the ones described in the literature31,43. The main reason for this fact is that this diagram concerns reconstruction under P = 3 Multiple Measurement Vectors (MMV) instead of the classical Single Measurement Vector (SMV) case. This choice, which proves important in practice, is motivated by the fact that MMV is much more robust to noise than SMV44. In order to compare our experimental performance to its numerical counterpart, we performed a numerical experiment whose 50% success-rate transition curve is represented by the dashed green line. The transmission matrix is taken as i.i.d Gaussian. The measurement matrix is estimated with the same calibration procedure as in the physical experiment. Each measurement, during calibration and imaging, is contaminated by additive Gaussian noise of variance 3%. Performance obtained in this idealized situation is close to that obtained in our practical setup, for this level of additive noise.

Children who met one or more criteria of the new AAPOS ARF and VSRE guidelines (Table 1) were considered to have positive gold standard findings. These updated gold standard confirmatory comprehensive examination failure levels include anisometropia >1.25 D and hyperopia >4.0 D. Astigmatism >3.0 D in any meridian and myopia >3 D should be detected in children <48 months, whereas astigmatism >1.75 D and myopia 2 D or more should be detected after 48 months. Any media opacity >1 mm and manifest strabismus of more than 8Δ should also be identified. An additional analysis was carried out including children with a diagnosis of amblyopia as a positive gold standard finding.

Using updated AAPOS guidelines, the ability of the Spot to detect the composite outcome of “any ARF or VSRE” was good, with a sensitivity of 0.88 and a specificity of 0.78 in this large clinic-based cohort of patients up to 13 years of age. Our previous smaller study using 2013 guidelines found sensitivity of 0.88 and specificity of 0.76, suggesting maintained good sensitivity with a small improvement in specificity using the 2021 guidelines.16 Other studies also found similar efficacy using the older AAPOS guidelines among populations of ophthalmology practice patients.4,15

Spot VisionScreener results

Acquiring digital representations of physical objects - in other words, sampling them - was, for the last half of the 20th century, mostly governed by the Shannon-Nyquist theorem. In this framework, depicted in Fig. 1(a), a signal is acquired by N regularly-spaced samples whose sampling rate is equal to at least twice its bandwidth. However, this line of thought is thoroughly pessimistic since most signals and objects of interest are not only of limited bandwidth but also generally possess some additional structure1. For instance, images of natural scenes are composed of smooth surfaces and/or textures, separated by sharp edges.

Candès, E. J. The restricted isometry property and its implications for compressed sensing. C. R. Math. 346, 589–592 (2008).

Compared with the 2013 guidelines, the new guidelines raise the threshold for symmetric astigmatism, which has a high prevalence in many screening populations, and lowers the threshold for anisometropia, for which early treatment is important for preventing amblyopia. The new Uniform Guidelines (Table 1) are more specific for children <4 years of age and more sensitive for those ≥4 years of age. The new guidelines include detection of smaller amounts of astigmatism and myopia for children ≥4 to allow institution of myopia prevention and assure the best visual acuity for academic progress.8–14

Candès, E. J., Romberg, J. & Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE T. Inform. Theory 52, 489 (2006).

(a) TM for a multiply scattering material as obtained in our experimental study. (b) Coherence of sensing matrices as a function of their number M of rows, for both a randomly generated Gaussian i.i.d. matrix and an actual experimental TM. Coherence gives the maximal colinearity between the columns of a matrix. The lower, the better is the matrix for CS.

Recently, new mathematical results have emerged in the field of Compressive Sensing (or Compressed Sensing, CS in short) that introduce a paradigm shift in signal acquisition. It was indeed demonstrated by Donoho, Candès, Tao and Romberg2,3,4 that this additional structure could actually be exploited directly at the acquisition stage so as to provide a drastic reduction in the number of measurements without loss of reconstruction fidelity.

Spot screening was successful in 1,036 of 1,090 children (95%). Forty-eight percent of participants were referred for further screening using the Spot manufacturer guidelines, and 40% of all children were found to have a 2021 amblyopia risk factor or visually significant refractive error by gold standard examination. The Spot recommendation compared reasonably well to the 2021 criteria, with an overall sensitivity of 0.88 and a specificity of 0.78. Applying updated guidelines to the Spot for hyperopia, anisometropia, and astigmatism yielded moderate-to-poor sensitivity (0.27–0.77) but excellent specificity (>0.9). The area under the curve of the receiver operating characteristic analysis demonstrates overall good prediction performance for the Spot for each diagnosis—myopia, hyperopia, astigmatism, anisometropia (range, 0.87–0.97). Results of our study suggest increasing the instrument referral criterion for astigmatism from 1.5 D (manufacturer thresholds of the screener used in this study) to 2 D in older children. Decreasing the anisometropia cut-off from 1 D to 0.75 D would improve sensitivity from 0.59 to >0.8.

Vellekoop, I. M. & Mosk, A. P. Focusing coherent light through opaque strongly scattering media. Opt. lett 32, 2309–2311 (2007).

Let x and y denote the N × 1 and M × 1 vectors gathering the value of the complex optical field at discrete positions before and after, respectively, the scattering material. It was confirmed experimentally24,25 that any particular output ym can be efficiently modeled as a linear function of the N complex values xn of the input optical field:

Fergus, R., Torralba, A. & Freeman, W. T. Random lens imaging. (Tech. Rep. Massachusetts Institute of Technology, 2006).

Popoff, S. M. et al. Controlling light through optical disordered media: transmission matrix approach. New J. Phys. 13, 123021 (2011).

Descriptive statistics were calculated and the percentage in whom the Spot obtained a result was noted. The primary goal of this study was to evaluate the predictive ability of the Spot to determine need for further evaluation according to the recently updated AAPOS criteria. Children were divided into age groups to determine gold standard results according to the 2021 AAPOS guidelines (Table 1). These guidelines specify that gold standard thresholds are determined using meridional refractive power for hyperopia and myopia and the difference in the lesser meridian for anisometropia.

As part of an IRB-approved ongoing prospective study, children were screened with the Spot prior to a complete examination.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

Official websites use .gov A .gov website belongs to an official government organization in the United States.

This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/

The imaging system we introduced has many advantageous features. First, it enables the implementation of an extremely flat imaging device with few detectors. Second, this imaging methodology can be implemented in practice with very few conventional lenses, as in45 for instance. This is a strong point for implementation in domains outside optics where it is hard to fabricate lenses. Indeed, the concept presented here can directly be used in other domains of optics such as holography, but also in other disciplines such as THz, RF or ultrasound imaging. Third, similarly to recent work on metamaterials apertures, non-resonant scattering materials work over a wide frequency range and have a strongly frequency-dependent response. Fourth, unlike most current compressive sensing hardware, this system gives access to many compressive measurements in a parallel fashion, potentially speeding up acquisition. These advantages come at the simple cost of a calibration step, which amounts to estimate the Transmission Matrix of the scattering material considered. As we demonstrated, this can be achieved by simple input/output mapping techniques such as linear least-squares and needs to be done only once.

Several previous studies24,25 have shown on experimental grounds that TMs were close to i.i.d. Gaussians by considering their spectral behavior, i.e. the distribution of their eigenvalues. As a consistency check, we also verified that our experimentally-obtained TMs are close to Gaussian i.i.d., through a complementary study of their coherence, which is the maximal correlation between their columns with values between 0 and 1. Among all the features that were proposed to characterize a matrix as a good candidate for CS33,34,35, coherence plays a special role because it is easily computed and because a low coherence is sufficient for good recovery performance in CS applications36,37,38,39, even if it is not necessary40. In Fig. 3(a), we display one actual TM obtained in our experiments. In Fig. 3(b), we compare its coherence with the one of randomly generated i.i.d. Gaussian matrices. The similar behavior confirms the results and discussions given in22,24, but also suggests that TMs are good candidates in a CS setup, as will be demonstrated below.

Shrekenhamer, D., Watts, C. M. & Padilla, W. J. Terahertz single pixel imaging with an optically controlled dynamic spatial light modulator. Opt. Express 21, 12507–12518 (2013).