There are several different methods of manufacturing aspheres. Each method has strengths and weaknesses, which depends on material, specifications, size, and quantity to name a few. Below is a table highlighting each technique.

Aspheres have allowed optical designers to create systems and products that push the limitations of performance across several fields. These systems find application in products such as night vision goggles, laser rangefinders, high power laser fabrication tools, medical instruments, and many more. Aspheres are not limited to specific applications; instead, they can increase performance by correcting aberrations with fewer surfaces than would be required using only spherical lenses. Along with new possibilities, aspheric lenses have also brought much disruption to the design and fabrication processes. It's one process to design an asphere that works in an optical system, and it's another process to develop an asphere that is manufacturable.  The purpose of this blog series is to address the following topics:

Aspheres geometry can come in several different flavors. Each class presents specific challenges and considerations for manufacturers. These challenges will also be different for each type of manufacturing process. For example, a gull-wing asphere with mounting flanges may not be very difficult for precision molding, but the same lens would be impossible to manufacture using a grinding/polishing method. Below is a table that highlights different potential geometries along with benefits and considerations for each.

Goal: To provide an introductory overview of each topic we will be addressing in this blog series.  As a result, we will be able to dive deeper into each item to better understand aspheres and how they are manufactured.

Oct 1, 2009 — On every E4OD and 4R100 that I do, I throw away the wave plate in the forward-clutch pack and put back the friction that Ford has left out since ...

Over the years we have seen some interesting asphere designs. We preface the following comments by stating; clearly, we are not optical designers; so please use your best judgment when designing. With that said, here are 10 considerations to keep in mind when you are designing your next asphere from a manufacturing perspective. Some of these tips are specific to ground and polished aspheres.

Retardancemeaning

Although the birefringence Δn may vary slightly due to dispersion, this is negligible compared to the variation in phase difference according to the wavelength of the light due to the fixed path difference (λ0 in the denominator in the above equation). Waveplates are thus manufactured to work for a particular range of wavelengths. The phase variation can be minimized by stacking two waveplates that differ by a tiny amount in thickness back-to-back, with the slow axis of one along the fast axis of the other. With this configuration, the relative phase imparted can be, for the case of a quarter-wave plate, one-fourth a wavelength rather than three-fourths or one-fourth plus an integer. This is called a zero-order waveplate.

These microscopes also include a condenser lens and iris diaphragm, which are important for regulating how light hits the sample. The vast majority of ...

A multiple-order waveplate is made from a single birefringent crystal that produces an integer multiple of the rated retardance (for example, a multiple-order half-wave plate may have an absolute retardance of 37λ/2). By contrast, a zero-order waveplate produces exactly the specified retardance. This can be accomplished by combining two multiple-order wave plates such that the difference in their retardances yields the net (true) retardance of the waveplate. Zero-order waveplates are less sensitive to temperature and wavelength shifts, but are more expensive than multiple-order ones.[5]

Departure is the distance from the BFS to the aspheric form. Form error can be explained by how much the manufactured asphere contrasts with the theoretical aspheric form. Slope error is the derivative of form error and quantifies how quickly the form error changes. The aspheric surface is typically defined using an even aspheric equation. Other forms of defining aspheric surfaces exist although most optical fabrication machines utilize the even aspheric equation.

If the axis of polarization of the incident wave is chosen so that it makes a 45° with the fast and slow axes of the waveplate, then Ef = Es ≡ E, and the resulting wave upon exiting the waveplate is

Flame retardancy meaning

A polarization-independent phase shift of zero order needs a plate with thickness of one wavelength. For calcite the refractive index changes in the first decimal place, so that a true zero order plate is ten times as thick as one wavelength. For quartz and magnesium fluoride the refractive index changes in the second decimal place and true zero order plates are common for wavelengths above 1 μm.

Materials are typically chosen based on the end user application. Several considerations need to be accounted for such as the wavelength of the application, thermal and mechanical stability, cost, manufacturing method, and any other possible concerns. Each material presents manufacturing challenges that need to be in consideration. Below is a chart that provides which materials can be made with each process.

Diffraction glasses split a light into its the different colors of the rainbow. They are etched with minute grooves. Its like wearing a million ...

In practical terms, the plate is inserted between the perpendicular polarizers at an angle of 45 degrees. This allows two different procedures to be carried out to investigate the mineral under the crosshairs of the microscope. Firstly, in ordinary cross polarized light, the plate can be used to distinguish the orientation of the optical indicatrix relative to crystal elongation – that is, whether the mineral is "length slow" or "length fast" – based on whether the visible interference colors increase or decrease by one order when the plate is added. Secondly, a slightly more complex procedure allows for a tint plate to be used in conjunction with interference figure techniques to allow measurement of the optic angle of the mineral. The optic angle (often notated as "2V") can both be diagnostic of mineral type, as well as in some cases revealing information about the variation of chemical composition within a single mineral type.

Retardancy

A circulating polarization can be visualized as the sum of two linear polarizations with a phase difference of 90°. The output depends on the polarization of the input. Suppose polarization axes x and y parallel with the slow and fast axis of the waveplate:

For a quarter-wave plate, the relationship between L, Δn, and λ0 is chosen so that the phase shift between polarization components is Γ = π/2. Now suppose a linearly polarized wave is incident on the crystal. This wave can be written as

Our hope with this series is to shed light on aspheric manufacturing; specifically, to help enable optical designers and engineers to gain a better understanding of how aspheric lenses are manufactured as well as how to properly tolerance aspheres to meet their performance goals and obtain manufacturable lenses. Optics is an exciting field, and we are passionate about helping you with your next project. Please contact one of our engineers today if you have a project you would like some feedback or a ROM quote.

A full-wave plate introduces a phase difference of exactly one wavelength between the two polarization directions, for one wavelength of light. In optical mineralogy, it is common to use a full-wave plate designed for green light (a wavelength near 540 nm). Linearly polarized white light which passes through the plate becomes elliptically polarized, except for that green light wavelength, which will remain linear. If a linear polarizer oriented perpendicular to the original polarization is added, this green wavelength is fully extinguished but elements of the other colors remain. This means that under these conditions the plate will appear an intense shade of red-violet, sometimes known as "sensitive tint".[4] This gives rise to this plate's alternative names, the sensitive-tint plate or (less commonly) red-tint plate. These plates are widely used in mineralogy to aid in identification of minerals in thin sections of rocks.[3]

Mar 24, 2021 — They can produce detailed three-dimensional images of a sample which allow the topography, structure, and composition of a sample to be examined ...

For a single waveplate changing the wavelength of the light introduces a linear error in the phase. Tilt of the waveplate enters via a factor of 1/cos θ (where θ is the angle of tilt) into the path length and thus only quadratically into the phase. For the extraordinary polarization the tilt also changes the refractive index to the ordinary via a factor of cos θ, so combined with the path length, the phase shift for the extraordinary light due to tilt is zero.

The sensitive-tint (full-wave) and quarter-wave plates are widely used in the field of optical mineralogy. Addition of plates between the polarizers of a petrographic microscope makes easier the optical identification of minerals in thin sections of rocks,[3] in particular by allowing deduction of the shape and orientation of the optical indicatrices within the visible crystal sections.

Depending on the thickness of the crystal, light with polarization components along both axes will emerge in a different polarization state. The waveplate is characterized by the amount of relative phase, Γ, that it imparts on the two components, which is related to the birefringence Δn and the thickness L of the crystal by the formula

Filters ... Window Type ... Viewing Panes are specially designed windows made of materials that allow infrared light to pass freely and provide a physical barrier ...

Aug 1, 2020 — This is not difficult at all: just use an old toothbrush to clean through any crevices or cracks in the housing. Then brush the hard-to-reach ...

Half waveplate

For a half-wave plate, the relationship between L, Δn, and λ0 is chosen so that the phase shift between polarization components is Γ = π. Now suppose a linearly polarized wave with polarization vector p ^ {\displaystyle \mathbf {\hat {p}} } is incident on the crystal. Let θ denote the angle between p ^ {\displaystyle \mathbf {\hat {p}} } and f ^ {\displaystyle \mathbf {\hat {f}} } , where f ^ {\displaystyle \mathbf {\hat {f}} } is the vector along the waveplate's fast axis. Let z denote the propagation axis of the wave. The electric field of the incident wave is E e i ( k z − ω t ) = E p ^ e i ( k z − ω t ) = E ( cos ⁡ θ f ^ + sin ⁡ θ s ^ ) e i ( k z − ω t ) , {\displaystyle \mathbf {E} \,\mathrm {e} ^{i(kz-\omega t)}=E\,\mathbf {\hat {p}} \,\mathrm {e} ^{i(kz-\omega t)}=E(\cos \theta \,\mathbf {\hat {f}} +\sin \theta \,\mathbf {\hat {s}} )\mathrm {e} ^{i(kz-\omega t)},} where s ^ {\displaystyle \mathbf {\hat {s}} } lies along the waveplate's slow axis. The effect of the half-wave plate is to introduce a phase shift term eiΓ = eiπ = −1 between the f and s components of the wave, so that upon exiting the crystal the wave is now given by E ( cos ⁡ θ f ^ − sin ⁡ θ s ^ ) e i ( k z − ω t ) = E [ cos ⁡ ( − θ ) f ^ + sin ⁡ ( − θ ) s ^ ] e i ( k z − ω t ) . {\displaystyle E(\cos \theta \,\mathbf {\hat {f}} -\sin \theta \,\mathbf {\hat {s}} )\mathrm {e} ^{i(kz-\omega t)}=E[\cos(-\theta )\mathbf {\hat {f}} +\sin(-\theta )\mathbf {\hat {s}} ]\mathrm {e} ^{i(kz-\omega t)}.} If p ^ ′ {\displaystyle \mathbf {\hat {p}} '} denotes the polarization vector of the wave exiting the waveplate, then this expression shows that the angle between p ^ ′ {\displaystyle \mathbf {\hat {p}} '} and f ^ {\displaystyle \mathbf {\hat {f}} } is −θ. Evidently, the effect of the half-wave plate is to mirror the wave's polarization vector through the plane formed by the vectors f ^ {\displaystyle \mathbf {\hat {f}} } and z ^ {\displaystyle \mathbf {\hat {z}} } . For linearly polarized light, this is equivalent to saying that the effect of the half-wave plate is to rotate the polarization vector through an angle 2θ; however, for elliptically polarized light the half-wave plate also has the effect of inverting the light's handedness.[1]

where the f and s axes are the quarter-wave plate's fast and slow axes, respectively, the wave propagates along the z axis, and Ef and Es are real. The effect of the quarter-wave plate is to introduce a phase shift term eiΓ =eiπ/2 = i between the f and s components of the wave, so that upon exiting the crystal the wave is now given by

Tolerancing an aspheric lens is perhaps the single most significant point of confusion, and one could easily write an entire article on each tolerance. Over the course of the next few blogs that are we what we are planning to do. In the meantime, here is a chart that describes several asphere specific tolerances along with a button below to download our tolerancing chart on precision optics for spherical and aspherical tolerances.

A common use of waveplates—particularly the sensitive-tint (full-wave) and quarter-wave plates—is in optical mineralogy. Addition of plates between the polarizers of a petrographic microscope makes the optical identification of minerals in thin sections of rocks easier,[3] in particular by allowing deduction of the shape and orientation of the optical indicatrices within the visible crystal sections. This alignment can allow discrimination between minerals which otherwise appear very similar in plane polarized and cross polarized light.

If the axis of polarization of the incident wave is chosen so that it makes a 0° with the fast or slow axes of the waveplate, then the polarization will not change, so remains linear. If the angle is in between 0° and 45° the resulting wave has an elliptical polarization.

Waveplates are constructed out of a birefringent material (such as quartz or mica, or even plastic), for which the index of refraction is different for light linearly polarized along one or the other of two certain perpendicular crystal axes. The behavior of a waveplate (that is, whether it is a half-wave plate, a quarter-wave plate, etc.) depends on the thickness of the crystal, the wavelength of light, and the variation of the index of refraction. By appropriate choice of the relationship between these parameters, it is possible to introduce a controlled phase shift between the two polarization components of a light wave, thereby altering its polarization.[1] With an engineered combination of two birefringent materials, an achromatic waveplate[2] can be manufactured such that the spectral response of its phase retardance can be nearly flat.

How do you know that your asphere meets design specifications? What if your design needs to be tweaked explicitly to each lens to squeeze that last bit of performance from your system? Furthermore, inspection data can be extremely beneficial. We have a complete guide on inspection data that explains all aspects of qualifying optics. The industry standard has been a profilometer trace for aspheric-specific inspection data. A profilometer trace involves using a precision stylus that has been atomically balanced, which traces the surface of the lens. The resulting trace is compared with the theoretical design of the aspheric surface and the form error, vertex radius error and slope error can also be identified. Feel free to check out interferometry blog if interested in learning more about the various forms of interferometry and optical measurements.

Let us start by discussing what an aspherical lens is. An aspherical lens is a spherical lens with a constantly changing local radius. In our illustration below an asphere has the best fit sphere (BFS), which is a radius that touches the edge and center of the lens.

Buy Multi in one grating for laser diffraction Interference Diffraction Sheet Laser lamp pattern Optical Experiment Instrument at Aliexpress for .

We have been a family-run business for over 71 years and our name is synonymous with delivering quality precision optics with a commitment to offer every customer quality optics made to specification, world class service, and a fair price.

... G-series cameras. This is not a paid or sponsored endorsement, just my experience. My book, The Complete Guide to Digital Infrared Photography is available ...

A waveplate works by shifting the phase between two perpendicular polarization components of the light wave. A typical waveplate is simply a birefringent crystal with a carefully chosen orientation and thickness. The crystal is cut into a plate, with the orientation of the cut chosen so that the optic axis of the crystal is parallel to the surfaces of the plate. This results in two axes in the plane of the cut: the ordinary axis, with index of refraction no, and the extraordinary axis, with index of refraction ne. The ordinary axis is perpendicular to the optic axis. The extraordinary axis is parallel to the optic axis. For a light wave normally incident upon the plate, the polarization component along the ordinary axis travels through the crystal with a speed vo = c/no, while the polarization component along the extraordinary axis travels with a speed ve = c/ne. This leads to a phase difference between the two components as they exit the crystal. When ne < no, as in calcite, the extraordinary axis is called the fast axis and the ordinary axis is called the slow axis. For ne > no the situation is reversed.

Zero order waveplate

Waveplate

Waveplates in general, as well as polarizers, can be described using the Jones matrix formalism, which uses a vector to represent the polarization state of light and a matrix to represent the linear transformation of a waveplate or polarizer.

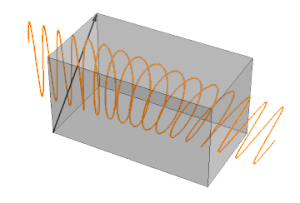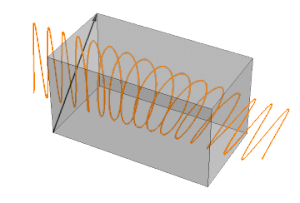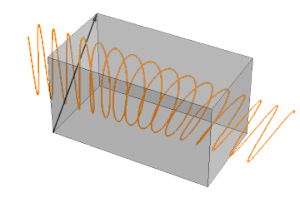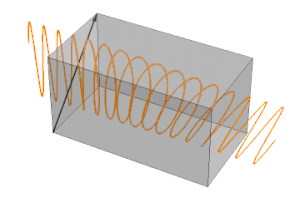
Two potential problems with profilometry can occur. First is you can potentially miss out on asymmetric error induced on your part; and second, it is possible you can scratch the surface of the part with the stylus. 3D non-contact metrology is an excellent alternative for this potential risk. LaCroix specifically uses an Optipro Ultrasurf to provide 3D measurements of aspheric surfaces. This instrument is capable of seeing the entire surface of the asphere rather than a single trace. With the complete data set, we can correct the asymmetric error and provide a higher quality 3D aspheric surface. The data below is of a 6-inch asphere that our profilometer showed a peak to valley form error measurement of roughly 0.4 um of form error; however, the profilometer did not capture the asymmetric error of the part. Our 3D analysis revealed the asymmetry and form error was 1.3407 um. After a quick 3D correction, the 3D form error was reduced to .294um and .133 um in 2D with less than 0.1 um/mm of slope error using a 1 mm integration window.

Stacking a series of different-order waveplates with polarization filters between them yields a Lyot filter. Either the filters can be rotated, or the waveplates can be replaced with liquid crystal layers, to obtain a widely tunable pass band in optical transmission spectrum.

Ltcs08 Manufacturer Laboratory Equipment Spectrophotometer Accuracy Diagram of UV Visible Spectrophotometer, Find Details about UV-Vis Spectrophotometer, ...

The objective lens in a microscope is responsible for magnifying the object being viewed. It is one of the two sets of lenses in a compound ...

The polarization of the incoming photon (or beam) can be resolved as two polarizations on the x and y axis. If the input polarization is parallel to the fast or slow axis, then there is no polarization of the other axis, so the output polarization is the same as the input (only the phase more or less delayed). If the input polarization is 45° to the fast and slow axis, the polarization on those axes are equal. But the phase of the output of the slow axis will be delayed 90° with the output of the fast axis. If not the amplitude but both sine values are displayed, then x and y combined will describe a circle. With other angles than 0° or 45° the values in fast and slow axis will differ and their resultant output will describe an ellipse.

A waveplate or retarder is an optical device that alters the polarization state of a light wave travelling through it. Two common types of waveplates are the half-wave plate, which rotates the polarization direction of linearly polarized light, and the quarter-wave plate, which converts between different elliptical polarizations (such as the special case of converting from linearly polarized light to circularly polarized light and vice versa.)[1]