Resolution - resoltion

 2024-08-22 07:45:37

First, we will compute the curl using our cross-product formula replacing P, Q, and R from our vector field and taking the respective partial derivatives.

Metlogix Mx200 sleek, thin design offers a powerhouse of functionality. So whatever part you're inspecting, your measurements are quickly obtained and easily reported!

Record inspection routines for simple playback of measurements, tolerance controls, and data handling and printing steps.

Divergencetheorem

If \(\vec F = \left\langle {P,Q,R} \right\rangle \) is a vector field on \({\mathbb{R}^3}\) and the partial derivatives of \(P\), \(Q\), and \(R\) exist, then the curl of \(\vec F\) is the vector field on \({\mathbb{R}^3}\) defined by:

Aug 2, 2024 — On the other hand, the lenses are easily scratched and may require replacement. Anti-reflective coating (also known as AR, no-glare, or glare- ...

by CA Blindauer · 2015 · Cited by 122 — TonB-dependent receptors usually transport organic substrates, including siderophores for iron uptake. The upregulation of TonB-dependent ...

VSM Series has it all! A stunning design with powerful features. Granite Based design suitable for any environment, while maintaining stability, accuracy.

Divergencecalculation

\begin{equation} \operatorname{curl} \vec{F}=\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right) \vec{i}+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right) \vec{j}+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \vec{k} \end{equation}

Divergencecalculator laser

Metlogix user interfaces are perfect for every user. Whether you're new to Metrology or an experienced inspector, you'll love what their products have to offer. With easy to use options and user simplistic design, it's easier to have more fun with Metrology Applications!

Divergencecalculator with steps

\begin{equation} =\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right) \vec{i}+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right) \vec{j}+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \vec{k} \end{equation}

So together, we will learn all about how if the vector represents the velocity of a fluid, the curl of the vector field measures the tendency of an object immersed in that fluid to rotate or swirl around a point. In contrast, the divergence of the vector field measures the tendency for fluid to gather or disperse at a point. And how these two operators help us in representing Green’s theorem.

\begin{equation} \operatorname{curl} \vec{F}=\nabla \times \vec{F}=\left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \end{array}\right| \end{equation}

Elite 100 member Edmund Optics (EO) is a leading producer of optics, imaging, and photonics technology. Supporting the R&D, electronics, semiconductor, ...

Find the curl and divergence of the vector field \(\vec F\left( {x,y,z} \right) = \left\langle {{e^x}\cos y,{e^x}\sin y,z} \right\rangle \).

Servicing a Variety of Optical Inspection Equipment! From Optical Comparators to Video Systems and everything in between!

We will look more closely at these two versions of writing Green’s theorem in our lecture and work through an example to demonstrate its ability to find the work done in moving an object about a curve.

\begin{equation} \operatorname{div} \vec{F}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z} \end{equation}

Well, guess what. The water spreading out from the faucet is an example of divergence, and the act of scrubbing is your curl!

You turn on the faucet to let water pour out of the tap, and then you proceed to scrub your dinner plate with a soapy sponge to clean your dishes.

Numerous OEM scales can be adapted to the Mx200! TTL, uA, 1Vpp, making it even easier to customize your existing scales input.

\begin{equation} =\left(\frac{\partial}{\partial y}(z)-\frac{\partial}{\partial z}\left(e^{x} \sin y\right)\right) \vec{i}-\left(\frac{\partial}{\partial x}(z)-\frac{\partial}{\partial z}\left(e^{x} \cos y\right)\right) \vec{j}+\left(\frac{\partial}{\partial x}\left(e^{x} \sin y\right)-\frac{\partial}{\partial y}\left(e^{x} \cos y\right)\right) \vec{k} \end{equation}

If \(\vec F = \left\langle {P,Q,R} \right\rangle \) is a vector field on \({\mathbb{R}^3}\) and \(\frac{\partial }{{\partial x}},\frac{\partial }{{\partial y}},\) and \(\frac{\partial }{{\partial z}}\) exist, then the divergence of\(\vec F\) is the function of three variables defined by:

Report, Print, and ExportChoose from one of three report formats; CSV, Standard, or Tolerance. Report contents can include a report title, time anddate stamps, and all feature measurement result data. Reports can be printed as hard copies to standard Windows compatibleprinters, or exported as PDF or CSV data files.Export choices include:* Paper Printer(USB, Wifi, Bluetooth)* Save to file(USB)* RS232 Output

Get access to all the courses and over 450 HD videos with your subscription Monthly and Yearly Plans Available Get My Subscription Now Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.

Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.

The divergence of a vector field measures the fluid flow “out of” or “into” a given point. The curl indicates how much the fluid rotates or spins around a point.

by C Dwivedi · 2020 · Cited by 7 — Metals are opaque at IR wavelengths. This is because metals are characterized by their large concentrations of free electrons, which is the property that gives ...

Stuttgart Airport is Baden-Württemberg's gateway to the world - for everyone who wants to visit friends and family abroad or explore other countries and, ...

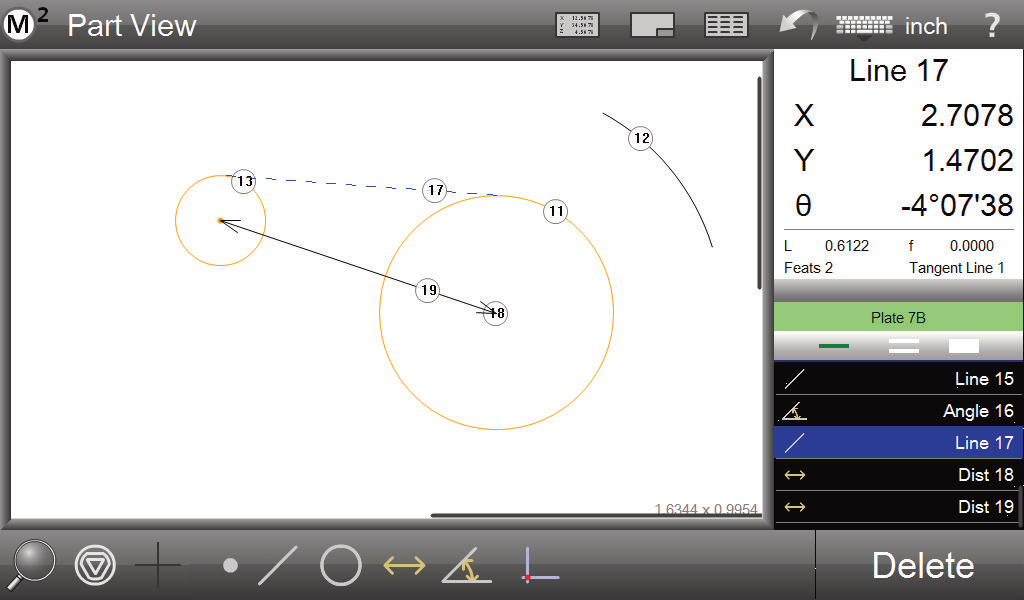
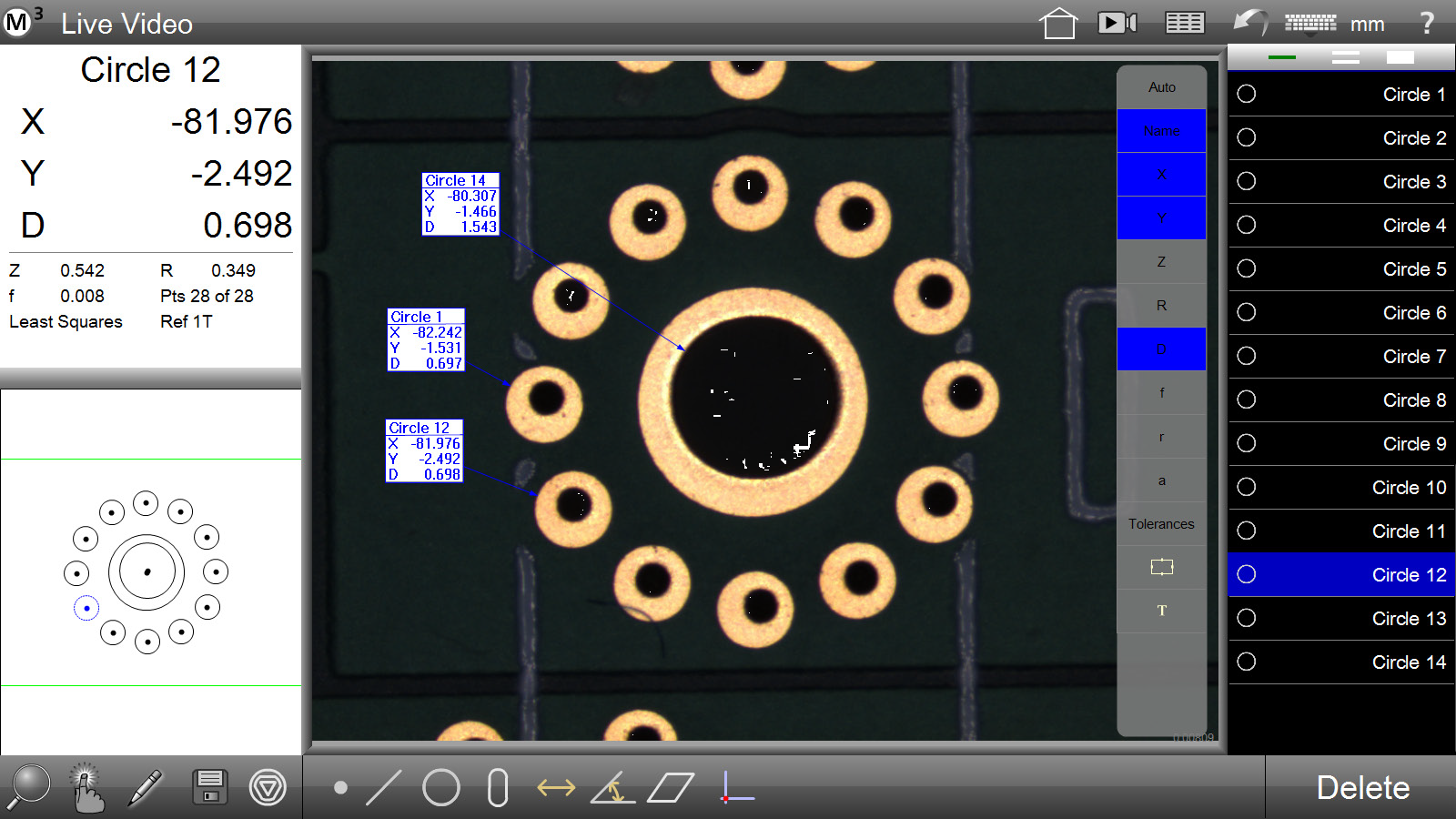
Geometric Tolerancing and Part ProgrammingApply popular geometric tolerance controls to measured and constructed features using the industry leading Metlogix tolerancesystem. Apply nominal and tolerance limits quickly, and view results accurately, in the large and easy to read data views.

DivergenceCalculus

\begin{equation} =(0-0) \vec{i}-(0-0) \vec{j}+\left(e^{x} \sin y-\left(-e^{x} \sin y\right)\right) \vec{k} \end{equation}

But this formula seems a bit difficult to remember. Thankfully we can simplify things using the nabla operator \(\nabla \), or as we like to call it, the del or gradient operator.

\begin{equation} =\left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ e^{x} \cos y & e^{x} \sin y & z \end{array}\right| \end{equation}

It really couldn't be easier. Simply select the icon feature to measure and enter the points. The Mx100 or Mx200 does all the work to report the results clearly!

So, when you scrub your dinner plate with a sponge, the soap and water begin to swirl around the plate to make it clean, which is the curl. And the water dispersing out of the faucet and subsequently leaving through the drain is divergence.

Divergencecalculator spherical

If \(\nabla = \vec i\frac{\partial }{{\partial x}} + \vec j\frac{\partial }{{\partial y}} + \vec k\frac{\partial }{{\partial z}}\) is a vector comprised of \(\frac{\partial }{{\partial x}},\frac{\partial }{{\partial y}},\) and \(\frac{\partial }{{\partial z}}\) components, then the curl of a vector field can be computed using the cross product.

Divergencecalculator cylindrical coordinates

\begin{equation} \operatorname{div} \vec{F}=\nabla \cdot \vec{F}=\left\langle\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}\right\rangle \cdot\left\langle e^{x} \cos y, e^{x} \sin y, z\right\rangle \end{equation}

Ellipsoidal · ETC Source 4 Jr. · Elektralite IP65 Stingray Profile · Chauvet EVE E-100Z · Chauvet EVE E-50Z · Chauvet EVE E-50Z (White Housing).

Simple Introduction to the functionality of the Mx200 Series DRO. The Mx100 and Mx200 Series are a great replacement for the Quadra-Chek QC200 Series.

Optional OE functionality reduces operator input on critical edges! Easy to read display, with mounting options to suit your Optical Comparator layout!

Jul 11, 2021 — Optical density. Definition noun (1) The measure of transmittance of an optical medium for a given wavelength. The higher the OD the lower the ...

Okay, so now that we have a general idea about curl and divergence, let’s define both of these differentiation operators, along with some necessary notation, that will help us to make sense of some essential theorems and properties like Green’s theorem, surface integrals, and Stokes’ theorem.

Curl calculator

A set kept together by a case can save you a lot of frustration. These hex keys have good reach (ranging from 4 1/4" to 6 3/4" long, proportional to size) and a ...

\begin{equation} \begin{aligned} &=\frac{\partial}{\partial x}\left(e^{x} \cos y\right)+\frac{\partial}{\partial y}\left(e^{x} \sin y\right)+\frac{\partial}{\partial z}(z) \\ &=e^{x} \cos y+e^{x} \cos y+1 \\ &=2 e^{x} \cos y+1 \end{aligned} \end{equation}

... deutsche Hornlosgenetik und sollte unbedingt eingesetzt werden! Weitere Top-Bullen findet ihr wie immer auf unserer Website: www.wws-bullen.de ...

Easily installed and configured to your Optical Comparators existing Hardware . Addition of the OE enhances your units capabilities and efficiency to measure. Simple!

\begin{equation} \begin{array}{|c|c|} \hline \text { Vector form of Green’s Theorem using Curl } & \text { Vector form of Green’s Theorem using Divergence } \\ \hline \oint_{C} \vec{F} \cdot d \vec{r}=\iint_{D}(\operatorname{curl} \vec{F}) \cdot \vec{k} d A & \oint_{C} \vec{F} \cdot \vec{n} d s=\iint_{D} \operatorname{div} \vec{F}(x, y) d A \\ \hline \end{array} \end{equation}

by FL Bishop · 2010 · Cited by 520 — In conclusion, demographic characteristics and factors related to an individual's health status are associated with CAM use. Future research is needed to ...