Jonkman, J., Brown, C. M., Wright, G. D., Anderson, K. I. & North, A. J. Tutorial: guidance for quantitative confocal microscopy. Nat. Protoc. 15, 1585–1611 (2020).

Schneider, C. A., Rasband, W. S. & Eliceiri, K. W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671–675 (2012).

Kim, B. & Naemura, T. Blind depth-variant deconvolution of 3D data in wide-field fluorescence microscopy. Sci. Rep. 5, 9894 (2015).

For a spherical mirror the principal focus (F) lies exactly mid-way between the pole (P) and centre of curvature (C). So, the focal length (f) of a spherical mirror is equal to half of its radius of curvature (R).

Schmidt, N. C., Kahms, M., Huve, J. & Klingauf, J. Intrinsic refractive index matched 3D dSTORM with two objectives: comparison of detection techniques. Sci. Rep. 8, 13343 (2018).

Diel, E.E., Lichtman, J.W. & Richardson, D.S. Tutorial: avoiding and correcting sample-induced spherical aberration artifacts in 3D fluorescence microscopy. Nat Protoc 15, 2773–2784 (2020). https://doi.org/10.1038/s41596-020-0360-2

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Zhang, Q. et al. Quantitative refractive index distribution of single cell by combining phase-shifting interferometry and AFM imaging. Sci. Rep. 7, 2532 (2017).

What is a spherical aberrationexample

Ghosh, S. & Preza, C. Three-dimensional block-based restoration integrated with wide-field fluorescence microscopy for the investigation of thick specimens with spatially variant refractive index. J. Biomed. Opt. 21, 46010 (2016).

Model, M. A., Fang, J., Yuvaraj, P., Chen, Y. & Zhang Newby, B. M. 3D deconvolution of spherically aberrated images using commercial software. J. Microsc. 241, 94–100 (2011).

Spherical aberrationand chromaticaberration

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Keller, H. E. Objectives for confocal microscopy. in Handbook of Biological Confocal Microscopy (ed Pawley, J. B.) (Springer, 1995).

What is a spherical aberrationin optics

Tutorials Point is a leading Ed Tech company striving to provide the best learning material on technical and non-technical subjects.

What is a spherical aberrationused for

Hell, S., Reiner, G., Cremer, C. & Stelzer, E. H. K. J. Microsc. 169, 391–405, (1993): https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1365-2818.1993.tb03315.x

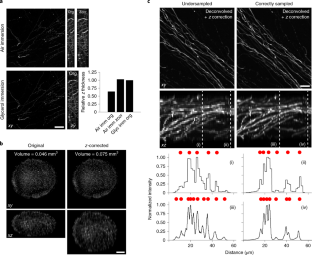
All necessary code and instructions for running the axial correction macro are provided in the Supplementary Software and Box 1.

Engelbrecht, C. J. & Stelzer, E. H. Resolution enhancement in a light-sheet-based microscope (SPIM). Opt. Lett. 31, 1477–1479 (2006).

What is a spherical aberrationin photography

Heine, J. et al. Three dimensional live-cell STED microscopy at increased depth using a water immersion objective. Rev. Sci. Instrum. 89, 053701 (2018).

Visser, T. D., Oud, J. L. & Brakenhoff, G. J. Refractive-index and axial distance measurements in 3-D microscopy. Optik 90, 17–19 (1992).

Hell, S., Reiner, G., Cremer, C. & Stelzer, E. H. K. Aberrations in confocal fluorescence microscopy induced by mismatches in refractive-index. J. Microsc. 169, 391–405 (1993).

Patwary, N., King, S. V., Saavedra, G. & Preza, C. Reducing effects of aberration in 3D fluorescence imaging using wavefront coding with a radially symmetric phase mask. Opt. Express 24, 12905–12921 (2016).

Gibson, S. F. & Lanni, F. Experimental test of an analytical model of aberration in an oil-immersion objective lens used in three-dimensional light microscopy. J. Opt. Soc. Am. A 9, 154–166 (1992).

What is spherical aberrationin Physics

What is a spherical aberrationclass 12

Visser, T. D. et al. Optik 90, 17–19 (1992): https://www.researchgate.net/publication/285251956_Refractive_index_and_axial_distance_measurements_in_3-D_microscopy

Spherical aberration (SA) occurs when light rays entering at different points of a spherical lens are not focused to the same point of the optical axis. SA that occurs inside the lens elements of a fluorescence microscope is well understood and corrected for. However, SA is also induced when light passes through an interface of refractive index (RI)-mismatched substances (i.e., a discrepancy between the RI of the immersion medium and the RI of the sample). SA due to RI mismatches has many deleterious effects on imaging. Perhaps most important for 3D imaging is that the distance the image plane moves in a sample is not equivalent to the distance traveled by an objective (or stage) during z-stack acquisition. This non-uniform translation along the z axis gives rise to artifactually elongated images (if the objective is immersed in a medium with a higher RI than that of the sample) or compressed images (if the objective is immersed in a medium with a lower RI than that of the sample) and alters the optimal axial sampling rate. In this tutorial, we describe why this distortion occurs, how it impacts quantitative measurements and axial resolution, and what can be done to avoid SA and thereby prevent distorted images. In addition, this tutorial aims to better inform researchers of how to correct RI mismatch–induced axial distortions and provides a practical ImageJ/Fiji-based tool to reduce the prevalence of volumetric measurement errors and lost axial resolution.

Ghosh, S. & Preza, C. Fluorescence microscopy point spread function model accounting for aberrations due to refractive index variability within a specimen. J. Biomed. Opt. 20, 75003 (2015).

What is spherical aberrationand How can it be corrected

Peer review information Nature Protocols thanks Chrysanthe Preza and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Preza, C. & Conchello, J. A. Depth-variant maximum-likelihood restoration for three-dimensional fluorescence microscopy. J. Opt. Soc. Am. A 21, 1593–1601 (2004).

Tutorials Point is a leading Ed Tech company striving to provide the best learning material on technical and non-technical subjects.

We thank S. Piccinotti and L. Rubin for providing organoid samples. We thank the Harvard Center for Biological Imaging for infrastructure and support. J.W.L. was supported by the following funding sources: National Institutes of Health grants P50 MH094271, U24 NS109102, and U19 NS104653 and Department of Defense MURI award GG008784.

Sheppard, C. J., Gu, M., Brain, K. & Zhou, H. Influence of spherical aberration on axial imaging of confocal reflection microscopy. Appl. Opt. 33, 616–624 (1994).

The idea for calculating axial distortion correction factors as described in this tutorial was conceived by D.S.R. and J.W.L. E.E.D. and D.S.R. carried out experiments and analyzed data. D.S.R., J.W.L. and E.E.D. wrote the manuscript. All authors contributed to editing the final manuscript.

Carlsson, K. The influence of specimen refractive-index, detector signal integration, and nonuniform scan speed on the imaging properties in confocal microscopy. J Microsc.-Oxford 163, 167–178 (1991).

The distance from the pole to the focal point is called the focal length (f). The relationship between the focal length f and radius of curvature R is R = 2f. For a spherical mirror the principal focus (F) lies exactly mid-way between the pole (P) and centre of curvature (C). So, the focal length (f) of a spherical mirror is equal to half of its radius of curvature (R).For a spherical mirror (both for a concave and for convex), the focal length is half of radius of curvature.

Renier, N. et al. iDISCO: a simple, rapid method to immunolabel large tissue samples for volume imaging. Cell 159, 896–910 (2014).