In astronomy, atomic diffusion is used to model the stellar atmospheres of chemically peculiar stars.[7][8] Diffusion of the elements is critical in understanding the surface composition of degenerate white dwarf stars and their evolution over time.[9]

For two different gases, A and B, with molecular masses mA, mB and molecular diameters dA, dB, the mean free path estimate of the diffusion coefficient of A in B and B in A is:

In Boltzmann's kinetics of the mixture of gases, each gas has its own distribution function, f i ( x , c , t ) {\displaystyle f_{i}(x,c,t)} , where t is the time moment, x is position and c is velocity of molecule of the ith component of the mixture. Each component has its mean velocity C i ( x , t ) = 1 n i ∫ c c f ( x , c , t ) d c {\textstyle C_{i}(x,t)={\frac {1}{n_{i}}}\int _{c}cf(x,c,t)\,dc} . If the velocities C i ( x , t ) {\displaystyle C_{i}(x,t)} do not coincide then there exists diffusion.

Jun 21, 2011 — Now I am searching a high resolution laser engraving service. (Edmund Optics asks between $120 and $1,250 for a glass target. I Want to know if ...

From the atomistic point of view, diffusion is considered as a result of the random walk of the diffusing particles. In molecular diffusion, the moving molecules in a gas, liquid, or solid are self-propelled by kinetic energy. Random walk of small particles in suspension in a fluid was discovered in 1827 by Robert Brown, who found that minute particle suspended in a liquid medium and just large enough to be visible under an optical microscope exhibit a rapid and continually irregular motion of particles known as Brownian movement. The theory of the Brownian motion and the atomistic backgrounds of diffusion were developed by Albert Einstein.[5] The concept of diffusion is typically applied to any subject matter involving random walks in ensembles of individuals.

∂ n ∂ t = D Δ n m   − ν ⋅ ∇ n m , {\displaystyle {\frac {\partial n}{\partial t}}=D\,\Delta n^{m}\ -\nu \cdot \nabla n^{m},}

In contrast, heat conduction through solid media is an everyday occurrence (for example, a metal spoon partly immersed in a hot liquid). This explains why the diffusion of heat was explained mathematically before the diffusion of mass.

How does aelectronmicroscope work

To view small objects even more closely, scientists use electron microscopes. These microscopes use beams of electrons instead of light to magnify objects. Electrons are some of the particles, or bits, that make up atoms. Electron beams cannot travel far in air. Objects must be put in a vacuum, or airless space, before they can be seen with an electron microscope.

In the scope of time, diffusion in solids was used long before the theory of diffusion was created. For example, Pliny the Elder had previously described the cementation process, which produces steel from the element iron (Fe) through carbon diffusion. Another example is well known for many centuries, the diffusion of colors of stained glass or earthenware and Chinese ceramics.

Diffusion of reagents on the surface of a catalyst may play an important role in heterogeneous catalysis. The model of diffusion in the ideal monolayer is based on the jumps of the reagents on the nearest free places. This model was used for CO on Pt oxidation under low gas pressure.

In 1858, Rudolf Clausius introduced the concept of the mean free path. In the same year, James Clerk Maxwell developed the first atomistic theory of transport processes in gases. The modern atomistic theory of diffusion and Brownian motion was developed by Albert Einstein, Marian Smoluchowski and Jean-Baptiste Perrin. Ludwig Boltzmann, in the development of the atomistic backgrounds of the macroscopic transport processes, introduced the Boltzmann equation, which has served mathematics and physics with a source of transport process ideas and concerns for more than 140 years.[13]

If a diffusion process can be described by Fick's laws, it is called a normal diffusion (or Fickian diffusion); Otherwise, it is called an anomalous diffusion (or non-Fickian diffusion).

The number A 1 ( ν ) {\displaystyle A_{1}({\nu })} is defined by quadratures (formulas (3.7), (3.9), Ch. 10 of the classical Chapman and Cowling book[13])

where F i {\displaystyle F_{i}} is the force applied to the molecules of the ith component and k T {\displaystyle k_{T}} is the thermodiffusion ratio.

In 1855, Adolf Fick, the 26-year-old anatomy demonstrator from Zürich, proposed his law of diffusion. He used Graham's research, stating his goal as "the development of a fundamental law, for the operation of diffusion in a single element of space". He asserted a deep analogy between diffusion and conduction of heat or electricity, creating a formalism similar to Fourier's law for heat conduction (1822) and Ohm's law for electric current (1827).

Aug 17, 2012 — There are 25.4 millimeters in one inch. Therefore to get amount of inches in millimeters, value in millimeters has to be divided by amount ...

Depth of field depends on aperture, focus distance, focal length and circle of confusion (CoC). The latter depends on camera sensor size, final image print size ...

There are several types of microscopes. Optical microscopes, also called light microscopes, work like magnifying glasses. They use lenses, which are curved pieces of glass or plastic that bend light. The object to be studied sits under a lens. As light passes from the object through the lens, the lens makes the object look bigger.

Each model of diffusion expresses the diffusion flux with the use of concentrations, densities and their derivatives. Flux is a vector J {\displaystyle \mathbf {J} } representing the quantity and direction of transfer. Given a small area Δ S {\displaystyle \Delta S} with normal ν {\displaystyle {\boldsymbol {\nu }}} , the transfer of a physical quantity N {\displaystyle N} through the area Δ S {\displaystyle \Delta S} per time Δ t {\displaystyle \Delta t} is

Here, all the indexes i, j, k = 0, 1, 2, ... are related to the internal energy (0) and various components. The expression in the square brackets is the matrix D i k {\displaystyle D_{ik}} of the diffusion (i,k > 0), thermodiffusion (i > 0, k = 0 or k > 0, i = 0) and thermal conductivity (i = k = 0) coefficients.

Under normal conditions, molecular diffusion dominates only at lengths in the nanometre-to-millimetre range. On larger length scales, transport in liquids and gases is normally due to another transport phenomenon, convection. To separate diffusion in these cases, special efforts are needed.

Solving this equation, one obtained the time-dependent diffusion constant in the long-time limit and when the particle is significantly denser than the surrounding fluid,[20]

The thermodynamic forces for the transport processes were introduced by Onsager as the space gradients of the derivatives of the entropy density s {\displaystyle s} (he used the term "force" in quotation marks or "driving force"):

How does a microscope workstep by step

and for p ∼ n γ {\displaystyle p\sim n^{\gamma }} Darcy's law gives the equation of diffusion in porous media with m = γ + 1.

All these effects are called diffusion because they describe the differences between velocities of different components in the mixture. Therefore, these effects cannot be described as a bulk transport and differ from advection or convection.

How does alightmicroscope workstep by step

Here R is the gas constant, T is the absolute temperature, n is the concentration, the equilibrium concentration is marked by a superscript "eq", q is the charge and φ is the electric potential.

In 1931, Lars Onsager[16] included the multicomponent transport processes in the general context of linear non-equilibrium thermodynamics. For multi-component transport,

where W {\displaystyle W} is intensity of any local source of this quantity (for example, the rate of a chemical reaction). For the diffusion equation, the no-flux boundary conditions can be formulated as ( J ( x ) , ν ( x ) ) = 0 {\displaystyle (\mathbf {J} (x),{\boldsymbol {\nu }}(x))=0} on the boundary, where ν {\displaystyle {\boldsymbol {\nu }}} is the normal to the boundary at point x {\displaystyle x} .

Explore the yucky side of science with the Crayola STEAM Gross Science Kit! This creative learning activity set includes supplies for 20 gross science ...

In chemistry and materials science, diffusion also refers to the movement of fluid molecules in porous solids.[6] Different types of diffusion are distinguished in porous solids. Molecular diffusion occurs when the collision with another molecule is more likely than the collision with the pore walls. Under such conditions, the diffusivity is similar to that in a non-confined space and is proportional to the mean free path. Knudsen diffusion occurs when the pore diameter is comparable to or smaller than the mean free path of the molecule diffusing through the pore. Under this condition, the collision with the pore walls becomes gradually more likely and the diffusivity is lower. Finally there is configurational diffusion, which happens if the molecules have comparable size to that of the pore. Under this condition, the diffusivity is much lower compared to molecular diffusion and small differences in the kinetic diameter of the molecule cause large differences in diffusivity.

In 1948, Wendell H. Furry proposed to use the form of the diffusion rates found in kinetic theory as a framework for the new phenomenological approach to diffusion in gases. This approach was developed further by F.A. Williams and S.H. Lam.[23] For the diffusion velocities in multicomponent gases (N components) they used

where J i {\displaystyle \mathbf {J} _{i}} is the flux of the i {\displaystyle i} th physical quantity (component), X j {\displaystyle X_{j}} is the j {\displaystyle j} th thermodynamic force and L i j {\displaystyle L_{ij}} is Onsager's matrix of kinetic transport coefficients.

Consider two gases with molecules of the same diameter d and mass m (self-diffusion). In this case, the elementary mean free path theory of diffusion gives for the diffusion coefficient

Biologists often use the terms "net movement" or "net diffusion" to describe the movement of ions or molecules by diffusion. For example, oxygen can diffuse through cell membranes so long as there is a higher concentration of oxygen outside the cell. However, because the movement of molecules is random, occasionally oxygen molecules move out of the cell (against the concentration gradient). Because there are more oxygen molecules outside the cell, the probability that oxygen molecules will enter the cell is higher than the probability that oxygen molecules will leave the cell. Therefore, the "net" movement of oxygen molecules (the difference between the number of molecules either entering or leaving the cell) is into the cell. In other words, there is a net movement of oxygen molecules down the concentration gradient.

Even LED lamps use UV to cure gel. The LED differentiation is that it's a different type of bulb than what was in older UV lamps.

where D i j = D j i ≥ 0 {\displaystyle D_{ij}=D_{ji}\geq 0} is a symmetric matrix of coefficients that characterize the intensities of jumps. The free places (vacancies) should be considered as special "particles" with concentration c 0 {\displaystyle c_{0}} .

In the Chapman–Enskog approximation, all the distribution functions are expressed through the densities of the conserved quantities:[13]

One common misconception is that individual atoms, ions or molecules move randomly, which they do not. In the animation on the right, the ion in the left panel appears to have "random" motion in the absence of other ions. As the right panel shows, however, this motion is not random but is the result of "collisions" with other ions. As such, the movement of a single atom, ion, or molecule within a mixture just appears random when viewed in isolation. The movement of a substance within a mixture by "random walk" is governed by the kinetic energy within the system that can be affected by changes in concentration, pressure or temperature. (This is a classical description. At smaller scales, quantum effects will be non-negligible, in general. Thus, the study of the movement of a single atom becomes more subtle since particles at such small scales are described by probability amplitudes rather than deterministic measures of position and velocity.)

The measurements of Graham contributed to James Clerk Maxwell deriving, in 1867, the coefficient of diffusion for CO2 in the air. The error rate is less than 5%.

Fick's first law: The diffusion flux, J {\displaystyle \mathbf {J} } , is proportional to the negative gradient of spatial concentration, n ( x , t ) {\displaystyle n(x,t)} :

A special type of optical microscope is a compound microscope. In a compound microscope a lens near the object makes a larger image (picture) of the object. This lens is called an objective lens. Another lens, known as the eyepiece, bends the light again. As a result, the eyepiece forms an even bigger image of the image made by the objective lens.

where J is the diffusion current density (amount of substance) per unit area per unit time, n (for ideal mixtures) is the electron density, x is the position [length].

Howdo microscopesworkPhysics

where n i {\displaystyle n_{i}} are the "thermodynamic coordinates". For the heat and mass transfer one can take n 0 = u {\displaystyle n_{0}=u} (the density of internal energy) and n i {\displaystyle n_{i}} is the concentration of the i {\displaystyle i} th component. The corresponding driving forces are the space vectors

For two gases, the difference between velocities, C 1 − C 2 {\displaystyle C_{1}-C_{2}} is given by the expression:[13]

Choose a language from the menu above to view a computer-translated version of this page. Please note: Text within images is not translated, some features may not work properly after translation, and the translation may not accurately convey the intended meaning. Britannica does not review the converted text.

At long time scales, Einstein's result is recovered, but short time scales, the ballistic regime are also explained. Moreover, unlike the Einstein approach, a velocity can be defined, leading to the Fluctuation-dissipation theorem, connecting the competition between friction and random forces in defining the temperature.[20]: 3.2

There are two ways to introduce the notion of diffusion: either a phenomenological approach starting with Fick's laws of diffusion and their mathematical consequences, or a physical and atomistic one, by considering the random walk of the diffusing particles.[3]

Under isothermal conditions T = constant. The relevant thermodynamic potential is the free energy (or the free entropy). The thermodynamic driving forces for the isothermal diffusion are antigradients of chemical potentials, − ( 1 / T ) ∇ μ j {\displaystyle -(1/T)\,\nabla \mu _{j}} , and the matrix of diffusion coefficients is

In 1920–1921, George de Hevesy measured self-diffusion using radioisotopes. He studied self-diffusion of radioactive isotopes of lead in the liquid and solid lead.

How does acompoundmicroscope work

Second, there is a "diffusion" process. The air arriving in the alveoli has a higher concentration of oxygen than the "stale" air in the alveoli. The increase in oxygen concentration creates a concentration gradient for oxygen between the air in the alveoli and the blood in the capillaries that surround the alveoli. Oxygen then moves by diffusion, down the concentration gradient, into the blood. The other consequence of the air arriving in alveoli is that the concentration of carbon dioxide in the alveoli decreases. This creates a concentration gradient for carbon dioxide to diffuse from the blood into the alveoli, as fresh air has a very low concentration of carbon dioxide compared to the blood in the body.

The coefficient D12 is positive. This is the diffusion coefficient. Four terms in the formula for C1−C2 describe four main effects in the diffusion of gases:

where the derivatives of s {\displaystyle s} are calculated at equilibrium n ∗ {\displaystyle n^{*}} . The matrix of the kinetic coefficients L i j {\displaystyle L_{ij}} should be symmetric (Onsager reciprocal relations) and positive definite (for the entropy growth).

How Does a microscope Workfor Kids

where μ is the chemical potential, μ0 is the standard value of the chemical potential. The expression a = exp ⁡ ( μ − μ 0 R T ) {\displaystyle a=\exp \left({\frac {\mu -\mu _{0}}{RT}}\right)} is the so-called activity. It measures the "effective concentration" of a species in a non-ideal mixture. In this notation, the Teorell formula for the flux has a very simple form[15]

where W i {\displaystyle W_{i}} is the net mass production rate in chemical reactions, ∑ i W i = 0 {\textstyle \sum _{i}W_{i}=0} .

The formalism of linear irreversible thermodynamics (Onsager) generates the systems of linear diffusion equations in the form

In these equations, the term ∇ ( ρ i V ) {\displaystyle \nabla (\rho _{i}V)} describes advection of the ith component and the term ∇ ( ρ i v i ) {\displaystyle \nabla (\rho _{i}v_{i})} represents diffusion of this component.

Yakov Frenkel (sometimes, Jakov/Jacob Frenkel) proposed, and elaborated in 1926, the idea of diffusion in crystals through local defects (vacancies and interstitial atoms). He concluded, the diffusion process in condensed matter is an ensemble of elementary jumps and quasichemical interactions of particles and defects. He introduced several mechanisms of diffusion and found rate constants from experimental data.

Electron microscopes can magnify objects up to 1 million times. This magnifying power makes electron microscopes very important scientific tools. However, they cannot be used to study living things because living things cannot survive in a vacuum.

How Does a microscope Worksimple

The simple but crucial difference between the Teorell formula and the Onsager laws is the concentration factor in the Teorell expression for the flux. In the Einstein–Teorell approach, if for the finite force the concentration tends to zero then the flux also tends to zero, whereas the Onsager equations violate this simple and physically obvious rule.

Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, as in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields beyond physics, such as statistics, probability theory, information theory, neural networks, finance, and marketing.

First, there is a "bulk flow" process. The lungs are located in the thoracic cavity, which expands as the first step in external respiration. This expansion leads to an increase in volume of the alveoli in the lungs, which causes a decrease in pressure in the alveoli. This creates a pressure gradient between the air outside the body at relatively high pressure and the alveoli at relatively low pressure. The air moves down the pressure gradient through the airways of the lungs and into the alveoli until the pressure of the air and that in the alveoli are equal, that is, the movement of air by bulk flow stops once there is no longer a pressure gradient.

where ρ i = m i n i {\displaystyle \rho _{i}=m_{i}n_{i}} is the mass concentration of the ith species, ρ = ∑ i ρ i {\textstyle \rho =\sum _{i}\rho _{i}} is the mass density.

The size of an image depends on the lenses used. For example, an objective lens might make an object appear 10 times larger than it really is. This lens is said to have a magnification of 10×. If the eyepiece also has a magnification of 10×, the total magnification of the microscope is 10 times 10, or 100×.

PoE Injectors: Power over Ethernet Adapters for your networking and wireless essentials, indoor and outdoor access points.

Robert Boyle demonstrated diffusion in solids in the 17th century[11] by penetration of zinc into a copper coin. Nevertheless, diffusion in solids was not systematically studied until the second part of the 19th century. William Chandler Roberts-Austen, the well-known British metallurgist and former assistant of Thomas Graham studied systematically solid state diffusion on the example of gold in lead in 1896. :[12]

Halifax, Nova Scotia B3H0B7. MLS® Number: 202425340. Press Realty Inc.

For diffusion of gases in porous media this equation is the formalization of Darcy's law: the volumetric flux of a gas in the porous media is

Here, D i j {\displaystyle D_{ij}} is the diffusion coefficient matrix, D i ( T ) {\displaystyle D_{i}^{(T)}} is the thermal diffusion coefficient, f i {\displaystyle f_{i}} is the body force per unit mass acting on the ith species, X i = P i / P {\displaystyle X_{i}=P_{i}/P} is the partial pressure fraction of the ith species (and P i {\displaystyle P_{i}} is the partial pressure), Y i = ρ i / ρ {\displaystyle Y_{i}=\rho _{i}/\rho } is the mass fraction of the ith species, and ∑ i X i = ∑ i Y i = 1. {\textstyle \sum _{i}X_{i}=\sum _{i}Y_{i}=1.}

A gradient is the change in the value of a quantity; for example, concentration, pressure, or temperature with the change in another variable, usually distance. A change in concentration over a distance is called a concentration gradient, a change in pressure over a distance is called a pressure gradient, and a change in temperature over a distance is called a temperature gradient.

After translating an article, all tools except font up/font down will be disabled. To re-enable the tools or to convert back to English, click "view original" on the Google Translate toolbar.

The standard derivation of the activity includes a normalization factor and for small concentrations a = n / n ⊖ + o ( n / n ⊖ ) {\displaystyle a=n/n^{\ominus }+o(n/n^{\ominus })} , where n ⊖ {\displaystyle n^{\ominus }} is the standard concentration. Therefore, this formula for the flux describes the flux of the normalized dimensionless quantity n / n ⊖ {\displaystyle n/n^{\ominus }} :

Henry Eyring, with co-authors, applied his theory of absolute reaction rates to Frenkel's quasichemical model of diffusion.[14] The analogy between reaction kinetics and diffusion leads to various nonlinear versions of Fick's law.[15]

Sometime later, Carl Wagner and Walter H. Schottky developed Frenkel's ideas about mechanisms of diffusion further. Presently, it is universally recognized that atomic defects are necessary to mediate diffusion in crystals.[12]

"...gases of different nature, when brought into contact, do not arrange themselves according to their density, the heaviest undermost, and the lighter uppermost, but they spontaneously diffuse, mutually and equally, through each other, and so remain in the intimate state of mixture for any length of time."

Fick's law describes diffusion of an admixture in a medium. The concentration of this admixture should be small and the gradient of this concentration should be also small. The driving force of diffusion in Fick's law is the antigradient of concentration, − ∇ n {\displaystyle -\nabla n} .

Due to the conservation law, z = b − ∑ i = 1 n c i , {\displaystyle z=b-\sum _{i=1}^{n}c_{i}\,,} and we have the system of m diffusion equations. For one component we get Fick's law and linear equations because ( b − c ) ∇ c − c ∇ ( b − c ) = b ∇ c {\displaystyle (b-c)\,\nabla c-c\,\nabla (b-c)=b\,\nabla c} . For two and more components the equations are nonlinear.

POINT OF FOCUS. For a given subject distance, a telephoto lens captures the scene with a much shallower depth of field than does other lenses. Out of focus ...

The system includes several reagents A 1 , A 2 , … , A m {\displaystyle A_{1},A_{2},\ldots ,A_{m}} on the surface. Their surface concentrations are c 1 , c 2 , … , c m . {\displaystyle c_{1},c_{2},\ldots ,c_{m}.} The surface is a lattice of the adsorption places. Each reagent molecule fills a place on the surface. Some of the places are free. The concentration of the free places is z = c 0 {\displaystyle z=c_{0}} . The sum of all c i {\displaystyle c_{i}} (including free places) is constant, the density of adsorption places b.

The concept of diffusion is widely used in many fields, including physics (particle diffusion), chemistry, biology, sociology, economics, statistics, data science, and finance (diffusion of people, ideas, data and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection.

While Brownian motion of multi-molecular mesoscopic particles (like pollen grains studied by Brown) is observable under an optical microscope, molecular diffusion can only be probed in carefully controlled experimental conditions. Since Graham experiments, it is well known that avoiding of convection is necessary and this may be a non-trivial task.

where D is the diffusion coefficient, Φ is porosity, n is the concentration, m > 0 (usually m > 1, the case m = 1 corresponds to Fick's law).

If the matrix of diffusion coefficients is diagonal, then this system of equations is just a collection of decoupled Fick's equations for various components. Assume that diffusion is non-diagonal, for example, D 12 ≠ 0 {\displaystyle D_{12}\neq 0} , and consider the state with c 2 = ⋯ = c n = 0 {\displaystyle c_{2}=\cdots =c_{n}=0} . At this state, ∂ c 2 / ∂ t = D 12 Δ c 1 {\displaystyle \partial c_{2}/\partial t=D_{12}\,\Delta c_{1}} . If D 12 Δ c 1 ( x ) < 0 {\displaystyle D_{12}\,\Delta c_{1}(x)<0} at some points, then c 2 ( x ) {\displaystyle c_{2}(x)} becomes negative at these points in a short time. Therefore, linear non-diagonal diffusion does not preserve positivity of concentrations. Non-diagonal equations of multicomponent diffusion must be non-linear.[15]

A distinguishing feature of diffusion is that it depends on particle random walk, and results in mixing or mass transport without requiring directed bulk motion. Bulk motion, or bulk flow, is the characteristic of advection.[1] The term convection is used to describe the combination of both transport phenomena.

where D is the diffusion constant, μ is the "mobility", kB is the Boltzmann constant, T is the absolute temperature, and q is the elementary charge, that is, the charge of one electron.

Third, there is another "bulk flow" process. The pumping action of the heart then transports the blood around the body. As the left ventricle of the heart contracts, the volume decreases, which increases the pressure in the ventricle. This creates a pressure gradient between the heart and the capillaries, and blood moves through blood vessels by bulk flow down the pressure gradient.

Care must be taken to properly account for the porosity (Φ) of the porous medium in both the flux terms and the accumulation terms.[22] For example, as the porosity goes to zero, the molar flux in the porous medium goes to zero for a given concentration gradient. Upon applying the divergence of the flux, the porosity terms cancel out and the second equation above is formed.

The mobility-based approach was further applied by T. Teorell.[19] In 1935, he studied the diffusion of ions through a membrane. He formulated the essence of his approach in the formula:

where kB is the Boltzmann constant, T is the temperature, P is the pressure, ℓ {\displaystyle \ell } is the mean free path, and vT is the mean thermal speed:

By definition, the diffusion velocity of the ith component is v i = C i − V {\displaystyle v_{i}=C_{i}-V} , ∑ i ρ i v i = 0 {\textstyle \sum _{i}\rho _{i}v_{i}=0} . The mass transfer of the ith component is described by the continuity equation

We’ve been busy, working hard to bring you new features and an updated design. We hope you and your family enjoy the NEW Britannica Kids. Take a minute to check out all the enhancements!

where ( J , ν ) {\displaystyle (\mathbf {J} ,{\boldsymbol {\nu }})} is the inner product and o ( ⋯ ) {\displaystyle o(\cdots )} is the little-o notation. If we use the notation of vector area Δ S = ν Δ S {\displaystyle \Delta \mathbf {S} ={\boldsymbol {\nu }}\,\Delta S} then

The diffusion coefficient D {\displaystyle D} is the coefficient in the Fick's first law J = − D ∂ n / ∂ x {\displaystyle J=-D\,\partial n/\partial x} , where J is the diffusion flux (amount of substance) per unit area per unit time, n (for ideal mixtures) is the concentration, x is the position [length].

We can see that the dependence on T for the rigid spheres is the same as for the simple mean free path theory but for the power repulsion laws the exponent is different. Dependence on a total concentration n for a given temperature has always the same character, 1/n.

The Einstein relation (kinetic theory) connects the diffusion coefficient and the mobility (the ratio of the particle's terminal drift velocity to an applied force).[18] For charged particles:

The dimension of the diffusion flux is [flux] = [quantity]/([time]·[area]). The diffusing physical quantity N {\displaystyle N} may be the number of particles, mass, energy, electric charge, or any other scalar extensive quantity. For its density, n {\displaystyle n} , the diffusion equation has the form

where T is the absolute temperature and μ i {\displaystyle \mu _{i}} is the chemical potential of the i {\displaystyle i} th component. It should be stressed that the separate diffusion equations describe the mixing or mass transport without bulk motion. Therefore, the terms with variation of the total pressure are neglected. It is possible for diffusion of small admixtures and for small gradients.

The Einstein model neglects the inertia of the diffusing partial. The alternative Langevin equation starts with Newton's second law of motion:[20]

How does alightmicroscope work

by BK Pierscionek · 2012 · Cited by 126 — The refractive power of a lens is determined largely by its surface curvatures and the refractive index of its medium. These properties can also be used to ...

The magnification of a compound light microscope can go up to about 1,000×. This magnifying power makes it possible to study tiny living things such as bacteria, algae, protozoans, and many types of cells.

In applications to gas dynamics, the diffusion flux and the bulk flow should be joined in one system of transport equations. The bulk flow describes the mass transfer. Its velocity V is the mass average velocity. It is defined through the momentum density and the mass concentrations:

When the density of electrons in solids is not in equilibrium, diffusion of electrons occurs. For example, when a bias is applied to two ends of a chunk of semiconductor, or a light shines on one end (see right figure), electrons diffuse from high density regions (center) to low density regions (two ends), forming a gradient of electron density. This process generates current, referred to as diffusion current.

This is the so-called Teorell formula.[citation needed] The term "gram-ion" ("gram-particle") is used for a quantity of a substance that contains the Avogadro number of ions (particles). The common modern term is mole.

Below, to combine in the same formula the chemical potential μ and the mobility, we use for mobility the notation m {\displaystyle {\mathfrak {m}}} .

"Bulk flow" is the movement/flow of an entire body due to a pressure gradient (for example, water coming out of a tap). "Diffusion" is the gradual movement/dispersion of concentration within a body with no net movement of matter. An example of a process where both bulk motion and diffusion occur is human breathing.[2]

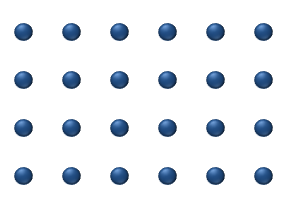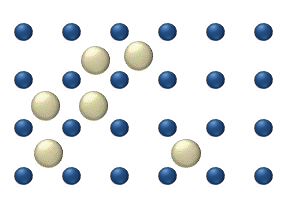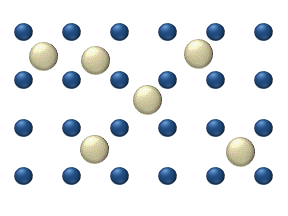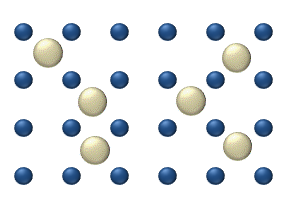
There is intrinsic arbitrariness in the definition of the thermodynamic forces and kinetic coefficients because they are not measurable separately and only their combinations ∑ j L i j X j {\textstyle \sum _{j}L_{ij}X_{j}} can be measured. For example, in the original work of Onsager[16] the thermodynamic forces include additional multiplier T, whereas in the Course of Theoretical Physics[17] this multiplier is omitted but the sign of the thermodynamic forces is opposite. All these changes are supplemented by the corresponding changes in the coefficients and do not affect the measurable quantities.

We can see that the diffusion coefficient in the mean free path approximation grows with T as T3/2 and decreases with P as 1/P. If we use for P the ideal gas law P = RnT with the total concentration n, then we can see that for given concentration n the diffusion coefficient grows with T as T1/2 and for given temperature it decreases with the total concentration as 1/n.

Jul 16, 2007 — Mode competition is the phenomenon that different resonator modes experience laser amplification in the same gain medium, ...

"... My long connection with Graham's researches made it almost a duty to attempt to extend his work on liquid diffusion to metals."

Dialysis works on the principles of the diffusion of solutes and ultrafiltration of fluid across a semi-permeable membrane. Diffusion is a property of substances in water; substances in water tend to move from an area of high concentration to an area of low concentration.[26] Blood flows by one side of a semi-permeable membrane, and a dialysate, or special dialysis fluid, flows by the opposite side. A semipermeable membrane is a thin layer of material that contains holes of various sizes, or pores. Smaller solutes and fluid pass through the membrane, but the membrane blocks the passage of larger substances (for example, red blood cells and large proteins). This replicates the filtering process that takes place in the kidneys when the blood enters the kidneys and the larger substances are separated from the smaller ones in the glomerulus.[26]

In the phenomenological approach, diffusion is the movement of a substance from a region of high concentration to a region of low concentration without bulk motion. According to Fick's laws, the diffusion flux is proportional to the negative gradient of concentrations. It goes from regions of higher concentration to regions of lower concentration. Sometime later, various generalizations of Fick's laws were developed in the frame of thermodynamics and non-equilibrium thermodynamics.[4]

A microscope is a device that magnifies tiny objects, or makes them look larger. People use microscopes to see objects that are too small to be seen with the eye alone. Such objects include cells, tiny living things, and grains of sand.

Analytical and numerical models that solve the diffusion equation for different initial and boundary conditions have been popular for studying a wide variety of changes to the Earth's surface. Diffusion has been used extensively in erosion studies of hillslope retreat, bluff erosion, fault scarp degradation, wave-cut terrace/shoreline retreat, alluvial channel incision, coastal shelf retreat, and delta progradation.[24] Although the Earth's surface is not literally diffusing in many of these cases, the process of diffusion effectively mimics the holistic changes that occur over decades to millennia. Diffusion models may also be used to solve inverse boundary value problems in which some information about the depositional environment is known from paleoenvironmental reconstruction and the diffusion equation is used to figure out the sediment influx and time series of landform changes.[25]

In modern science, the first systematic experimental study of diffusion was performed by Thomas Graham. He studied diffusion in gases, and the main phenomenon was described by him in 1831–1833:[10]