By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.

Thermal lensfor phone

Abstract: Thermal lensing is relevant in many solid-state bulk lasers and amplifiers. Here, a number of important questions on that topic are answered.

The Gaussian characteristics of the beam are essentially important in the vicinity of the beam waist. Indeed, when z increases, the complex radius of curvature becomes close to R and the wave could be considered spherical.

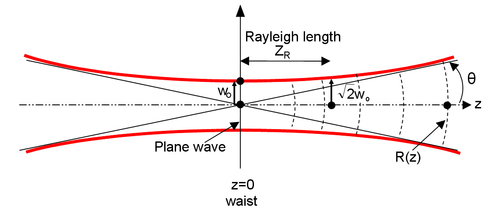
Let's take again the origin at the waist position w0, corresponding to a plane wave (infinite radius of curvature). We have defined the Rayleigh length : .

Thermal lensing is an effect occurring in laser gain media, which is relevant in many devices such as solid-state bulk lasers and amplifiers – particularly for operation at higher power levels. In many cases, it crucially limits the possible performance of such devices in terms of output power and beam quality.

Thermal lensspectroscopy

In many cases, thermal lensing essentially depends only on the average power of a pulsed laser and changes quite little during the generation of a laser pulse. However, this can be different in cases with quite high pulse energy. The gain medium made then heat up significantly during one pulse and/or during the pumping time before it. In the latter case, correspondingly more sophisticated simulation models are required.

Unfortunately, a top-hat pump beam is often not good in terms of conversion efficiency, while a Gaussian pump beam, for example, leads to stronger aberrations, which can eventually deteriorate the laser beam quality. At high power levels, some compromise is often unavoidable.

In a solid-state lasers, for example, thermal lensing can arise from three different effects, which are all caused by the heating and the resulting inhomogeneous temperature distribution in the laser crystal:

Note: this box searches only for keywords in the titles of articles, and for acronyms. For full-text searches on the whole website, use our search page.

This article is a posting of the Photonics Spotlight, authored by Dr. Rüdiger Paschotta. You may link to this page and cite it, because its location is permanent. See also the RP Photonics Encyclopedia.

Bestthermallenses

The main basic expressions related to Gaussian beams were mathematically obtained in the previous paragraph. We will now describe their physical signification.

Yes: if each laser crystal needs to convert only part of the laser power, the overall challenge of thermal lensing can be substantially reduced – provided that you use a clever resonator design of your laser resonator. For example, there are so-called periodic resonators.

w(z) is the dimension of the laser spot (the “radius” if the spot is circular) in the plane perpendicular to the propagation, at a distance z from the origin. Precisely, it is the radius (at 1/e for the amplitude, or 1/e² for the intensity) of the transverse Gaussian profile at the z abscissa.

In principle, one may avoid optical aberrations of the thermal lens by arranging for a homogeneous heat generation density. That may be achieved with a top-hat pump beam (or with side pumping), provided that the influence of the laser beam does not make it inhomogeneous again.

It is often said that fiber lasers have weak thermal lensing effects because the heat generation is distributed over a substantial length. As explained above, that reasoning is actually wrong. The overall strength of the thermal lens over the whole fiber length can be rather strong, only it usually cannot hurt you much in a fiber device. Ideally, you have a single-mode fiber where thermal lensing cannot do more than slightly shrinking the fiber mode. At kilowatt power levels, however, things get difficult also in fibers; thermal lensing is then one of several challenges – but usually not the worst one.

Yes, but this is also not trivial. Some people are sending a weak test laser beam through the gain medium and perform e.g. some wavefront analysis on that, but as the actual strong signal beam can substantially modify the temporal distribution, that should also be around during the measurement – which is tricky to do. There are various other methods, e.g. based on the measurement of mode properties, often requiring a specially designed laser resonator just for that test. Normally, it takes substantial expertise to measure the strength of the thermal lens accurately.

Thermal lensCamera

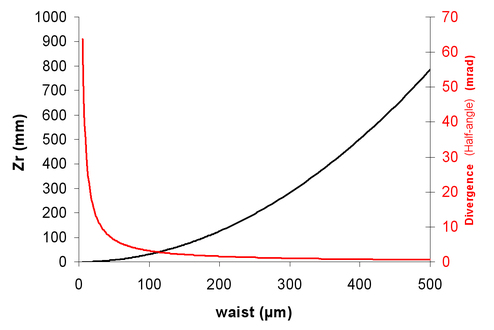
The Rayleigh length is the distance (from the waist) where the beam area is twice the beam area at the waist (the radius is times bigger). This parameter is useful to define a “collimated” beam : over this length, the beam size is nearly constant (between and ) - see figure 11.

Please do not enter personal data here. (See also our privacy declaration.) If you wish to receive personal feedback or consultancy from the author, please contact him, e.g. via e-mail.

Thermal lenscost

On the other hand, not knowing the strengths of your thermal lens means that you are fishing in the dark. You better have some reasonable quantitative understanding already in the planning phase, if thermal lensing must be expected be significant.

The divergence of a Gaussian beam is inversely proportional to the size of its waist. In the framework of Gaussian optics, “collimating a beam” is the same thing as “having a big waist”.

Note: the article keyword search field and some other of the site's functionality would require Javascript, which however is turned off in your browser.

For a tightly focused laser beam (w0 = 10 µ) and a 1 µm wavelength, we find ZR = 314 µm and a divergence (half-angle) of 1,8 degrees.

The size of the beam at the origin, w0, is minimal : the beam will diverge from this point (see figure 11). This minimal dimension is called “beam waist” (the waist is the radius of the spot. The diameter is of course given by 2 w0).

Thermal lenseffect

If you use a laser crystal of twice the length and with half the doping concentration, you can spread out the thermal lens over twice the length. The required higher pump beam quality may be an issue, though. More importantly, the total dioptric power of the thermal lens is not reduced – it is just spread out.

Fortunately, certain simplifications are in many cases quite reasonable and can substantially reduce the required effort. For example, the direct temperature effect on the refractive index (see above) is often dominant, so that one can neglect the other two effects, and in many cases we have an approximately radial heat flow, so that the temperature distribution can be calculated conveniently and quickly with a simple set of differential equations.

Thermalcameralensmaterial

If you increase the area of the pump beam of an end-pumped laser, the thermal lens indeed gets weaker. However, if you then need to increase the laser mode size (e.g. in order to maintain diffraction-limited beam quality), the larger laser mode gets more sensitive to lensing – and in the end your modification does not help you. By the way, the reduced pump intensity would also decrease the available laser gain.

A powerful method of reducing thermal lensing is to use a laser geometry where you largely avoid heat flow in the direction perpendicular to the laser beam. That principle is applied in thin-disk lasers. Interestingly, the thermal lens in a thin-disk laser is not that weak for a device operating at a low power level, but the scaling properties are very much more benign than for conventional laser geometries: the challenge from thermal lensing does not become substantially stronger as you scale up the power. Therefore, such lasers can be made to operate at very high power levels with excellent beam quality.

Thermal lensnikon

When z increases, the beam expands in the transverse direction while its amplitude on the z-axis decrease (energy conservation). The profile shape remains Gaussian.

If you want to place a link to this article in some other resource (e.g. your website, social media, a discussion forum, Wikipedia), you can get the required code here.

Here you can submit questions and comments. As far as they get accepted by the author, they will appear above this paragraph together with the author’s answer. The author will decide on acceptance based on certain criteria. Essentially, the issue must be of sufficiently broad interest.

If we consider a “big” waist (1 mm), we find ZR = 3,14 m and a divergence (half-angle) of 0,018 degrees. We then obtain a so-called “collimated beam”.

As long as dn/dT is constant, cooling does not help because the lensing is generated not by the temperature as such, but by temperature gradients. For operation at really low (cryogenic) temperatures – e.g., for cooling with liquid nitrogen – dn/dT is often reduced substantially, and thermal lensing indeed gets weaker accordingly.