The FOV is a crucial aspect of observational astronomy as it determines the range of celestial objects that can be observed. A larger FOV allows for the observation of larger celestial objects, such as nebulae and galaxies, while a smaller FOV is better suited for observing smaller objects, such as planets and stars.

In modern microscope eyepieces, the field diaphragm either precedes the optical system or is located between the lens element groups, as illustrated in Figure 1. This figure presents cutaway diagrams of a Ramsden and Huygens eyepiece showing ray traces through the field lens, eye lens, and field diaphragm. The Ramsden eyepiece (illustrated on the right in Figure 1) has an optical system consisting of two plano-convex lenses having a fixed separation distance according to their focal lengths. The first lens is termed the field lens because it is closer to the plane where the intermediate image is formed in the microscope. The field diaphragm is located between the tube opening and the field lens in the Ramsden eyepiece design.

What is the relationship between magnification anddepthof field

Will Kalif is an amateur astronomer at TelescopeNerd.com. Will is an author of the book "See It With A Small Telescope". Will Kalif has been passionate about telescopes and the wonders of the night sky ever since he received his first telescope as a teenager. And for several decades now he has been making and using his own telescopes and helping other people to also enjoy the various things that can be seen on a dark and starry night.

The field of view (FOV) in a telescope defines the extent of the observable universe that is visible through the eyepiece at any given moment. Knowing the FOV allows astronomers to determine the ideal eyepiece for a specific observation. There are two distinct types of FOV: the apparent field of view (AFOV) and the true field of view (TFOV).

The magnification of a telescope is determined by the ratio of the telescope’s focal length to the eyepiece’s focal length. Therefore, the choice of the eyepiece significantly affects the magnification and, consequently, the field of view and the types of celestial objects that can be observed effectively.

The field of view (FOV) in a telescope refers to the extent of the observable sky that can be viewed at a single point in time. It’s quantified in units such as degrees, arcminutes, or arcseconds, and is influenced by the telescope’s optics, encompassing factors like the diameter of the objective lens or mirror and the eyepiece in use.

What is the relationship between magnification and field of viewbrainly

The eyepiece of a telescope magnifies the image formed by the telescope’s objective lens or mirror. The eyepiece is the part of the telescope that observers look through. The eyepiece plays a significant role in determining the magnification, field of view (FOV), and overall viewing experience.

Magnification and field of view (FOV) in a telescope share an inverse relationship. This means that as the magnification increases, the FOV decreases, and conversely, as the magnification decreases, the FOV increases. This relationship stems from the fact that as one increases the magnification, the telescope effectively zooms in on a smaller section of the sky, thereby reducing the FOV.

Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.

What is the relationship between magnification andbrightness

To calculate the telescope FOV from focal length divide the eyepiece field stop (mm), or AFOV by the telescope’s focal length (mm), then multiplying by 57.3, as seen in the formula below.

If an auxiliary lens is inserted between the objective and eyepiece, the magnification factor of this lens should also be employed in the equation by multiplication with the objective magnification (prior to the division operation). Although the field number is usually limited by the magnification and field diaphragm (stop) size of the eyepiece, there is clearly a limit that is also imposed by the design of the objective lens system. In early microscope objectives, the maximum usable field diameter tended to be about 18 millimeters or considerably less, but with modern plan apochromats and other specialized flat-field objectives, the maximum usable field can sometimes exceed 28 millimeters.

With increasedmagnification whathappens tothe field of view

The Huygens eyepiece, illustrated on the left in Figure 1, is designed with the field lens positioned before the intermediate image plane, which coincides with the field diaphragm. Unlike the Ramsden eyepiece, the Huygens design has a focal point (at the intermediate image plane) residing between the eye and field lenses. In this case, the eye lens acts as a loupe to magnify the intermediate image.

The field number of typical eyepieces varies between 6 and 28 millimeters and (in general) decreases with the magnification of the eyepiece. For example, an eyepiece having a magnification of 10x typically has a field number ranging between 16 and 18 millimeters, while a lower magnification eyepiece (5x) has a field number of about 20 millimeters. Presented in Figure 2 is a comparison between the view fields available with similar eyepieces, one having a field number of 20 and the other a field number of 26. Note the greater range of specimen features visible through the eyepiece having the larger field number.

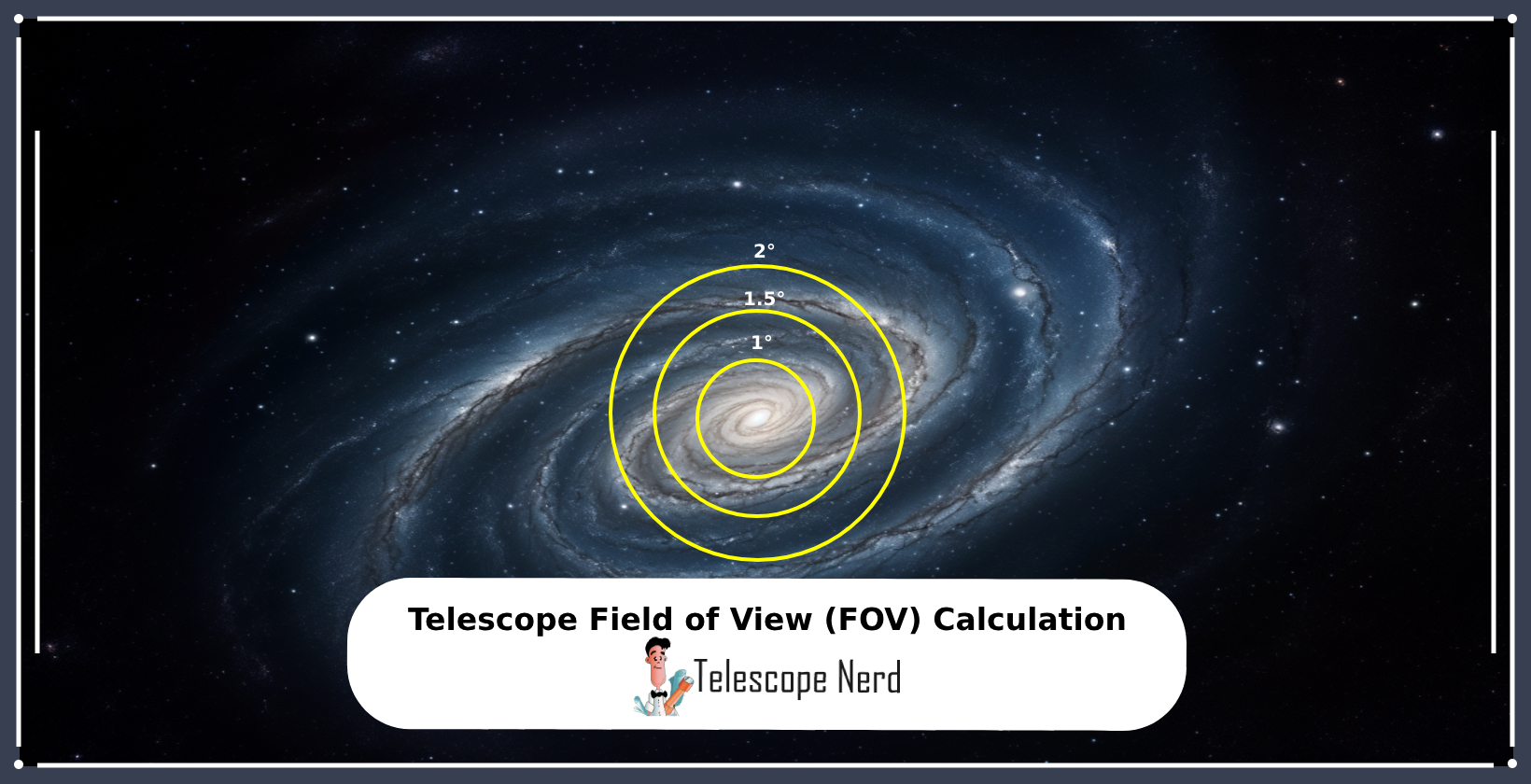
The field of view (FOV) of a telescope is calculated using either the eyepiece field of view and magnification, or the diameter of the field stop and focal length. The most common method to calculate the true field of view (TFOV) is to divide the apparent field of view (AFOV) by magnification, as seen in the formula below.

Calculation of the TFOV is done by dividing the AFOV of the eyepiece by the magnification of the telescope, or through the relationship of the focal lengths of the telescope and the eyepiece. The TFOV is typically expressed in degrees.

The eyepiece field stop refers to the diameter of the image formed by the telescope’s objective, while the telescope focal length is the distance from the objective to the point where it forms an image.

What is the relationship between magnification and field of viewquizlet

The ideal FOV for a telescope is contingent on the specifics of the observation. For example, a larger FOV will be more desirable for wide-field observations of large celestial bodies, while a smaller FOV will be more effective for detailed observations of smaller entities.

Asmagnificationincreases,thedepthof the field of view

The value 57.3 is used because there are 2π radians in a full circle of 360 degrees. Dividing 360° by 2π yields about 57.2958° per radian, allowing astronomers to calculate their TFOV in degrees. For example, a telescope with an eyepiece field stop diameter of 35mm, and a focal length of 1000mm will yield a 2.0055-degree TFOV. This equation is expressed as ([35 / 1000] x [57.3] = 2.0055).

The diameter of the field in an optical microscope is expressed by the field-of-view number, or simply the field number, which is the diameter of the view field in millimeters measured at the intermediate image plane.

The apparent field of view (AFOV) refers to the perceived expanse of the sky covered by the eyepiece, while the true field of view (TFOV) represents the actual segment of the sky visible through the telescope. To illustrate, an eyepiece with a broad AFOV will give the impression of a larger sky, but the actual TFOV is smaller due to the magnifying effect of the telescope.

The FOV of an eyepiece is calculated using the formula: FOV = (Eyepiece field stop / Eyepiece focal length) x 57.3. The eyepiece field stop is the diameter of the image formed by the eyepiece, and the eyepiece’s focal length is the distance from the eyepiece to the point where it forms an image. The factor of 57.3 is used to convert the result from radians to degrees.

The FOV of the eyepiece impacts the overall FOV of the telescope. An eyepiece with a larger FOV will yield a larger overall FOV for the telescope, facilitating the observation of larger celestial objects. On the other hand, an eyepiece with a smaller FOV will result in a smaller overall FOV, which is more suitable for observing smaller celestial bodies.

The size of the eyepiece field diaphragm opening is also dependent upon the correction for off-axial aberrations (coma, astigmatism, and lateral chromatic) of the objective. Recent eyepieces feature highly corrected glass that enables wide-field designs having field numbers of 26 millimeters and greater.

The optimal FOV for a telescope depends on the type of observations being made. For example, a larger FOV is preferable for wide-field observations of large celestial objects, while a smaller FOV is better for detailed observations of smaller objects. By understanding the relationship between FOV and viewing experience, astronomers are able to select the best eyepiece for their observational goals.

The field of view of a telescope eyepiece is the angular extent of the sky that is observed through the eyepiece. It is influenced by the eyepiece’s design and is typically provided by the manufacturer.

The magnification in a telescope is determined by the focal length of the telescope and the eyepiece. To calculate the magnification, divide the telescope focal length by the eyepiece focal length. For instance, if a telescope has a focal length of 1000mm and is used with an eyepiece with a focal length of 10mm, the magnification would be 1000 / 10 = 100x. At 100x magnification, the field of view would be smaller than at 50x magnification, because magnifying an image presents a smaller portion of the sky. This allows for more detailed observation of smaller celestial objects.

Asmagnificationincreases,thedepthof field

In all modern eyepiece designs, the field lens is placed a sufficient distance away from the intermediate image plane to ensure that dust or other surface debris and defects on the lens surface are not visualized along with the specimen. The top lens in both eyepiece designs is referred to as the eye lens because it is closest to the eye of the observer.

Nikon offers a range of eyepiece options featuring magnification and field of view combinations tailored towards a variety of applications.

The calculation of the TFOV involves dividing the AFOV by the magnification of the telescope. This calculation helps astronomers optimize their observations based on the specific characteristics of the celestial objects they wish to study.

Asmagnificationincreases,the field of viewdecreases

Astronomers can also use an online field of view calculator to compute the TFOV of a telescope based on the specifications of the telescope and eyepiece.

Though dividing AFOV by magnification is a simple and widely used method of calculation, it is not exact. Telescope optics vary in measurement by up to 5%, which skews the accuracy of the calculation. For a more accurate calculation, astronomers use the field stop diameter and focal length to calculate FOV.

The FOV in the eyepiece is determined by its specific AFOV, and the choice of eyepiece thereby plays a vital role in the observational experience. The relationship between FOV and magnification is inversely proportional, such that an increase in magnification results in a narrower field of view, while a decrease in magnification yields a broader view.

In most cases, the eyepiece field diaphragm opening diameter determines the view field size. The field size in the specimen plane is then defined as the field number divided by the magnification of the objective:

For example, if an eyepiece has a field of view, or AFOV, of 50 degrees and a magnification of 25x, the true field of view is 2 degrees. This equation is expressed as (50 / 25 = 2). Knowing the TFOV of a telescope is crucial to selecting the right optics based on specific observational goals, making it a crucial metric for astronomers.

The FOV plays a pivotal role in observational astronomy as it dictates the range of celestial objects that can be observed. For instance, a telescope with a larger FOV enables the viewing of expansive celestial bodies like nebulae and galaxies, whereas a telescope with a smaller FOV is more suitable for observing smaller entities like planets and stars.

Magnification in a telescope refers to the degree to which the image of an observed object is enlarged compared to the naked eye. It’s a crucial factor in observational astronomy as it affects the level of detail that is seen when observing celestial objects. Higher magnification allows for more detailed observation of smaller and distant objects, while lower magnification is better for larger or closer objects.

When calculating FOV, it’s important to distinguish the difference between the apparent field of view (AFOV) and the true field of view (TFOV). The AFOV is the angle of the sky that appears to be covered by the eyepiece, while the TFOV is the actual portion of the sky that is seen through the telescope. For example, a wide AFOV eyepiece will make the sky appear larger, but the actual TFOV is smaller due to the telescope’s magnification.