Acceptance angle

Now the numerical aperture is usually the $\sin$ of the angle - so if you care about the difference (which is important as NA gets larger) you need to do a bit of math:

I am not absolutely sure that these formulas work for compound lenses... perhaps somebody can either confirm this or point out the correction that is needed.

But that’s not all. You can also calculate the volume of a prism by multiplying the area of the base by the height of the prism.

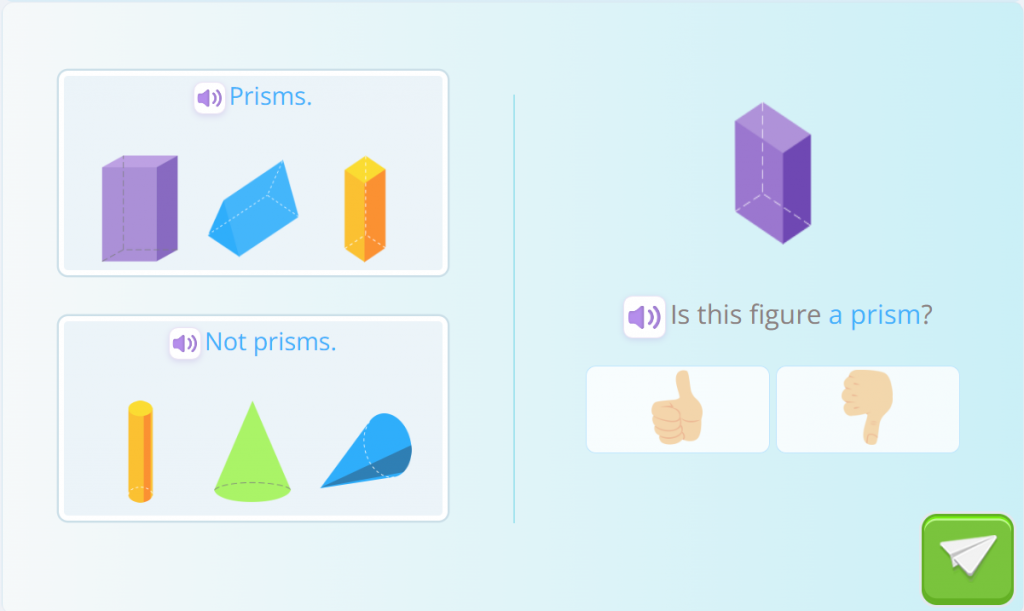
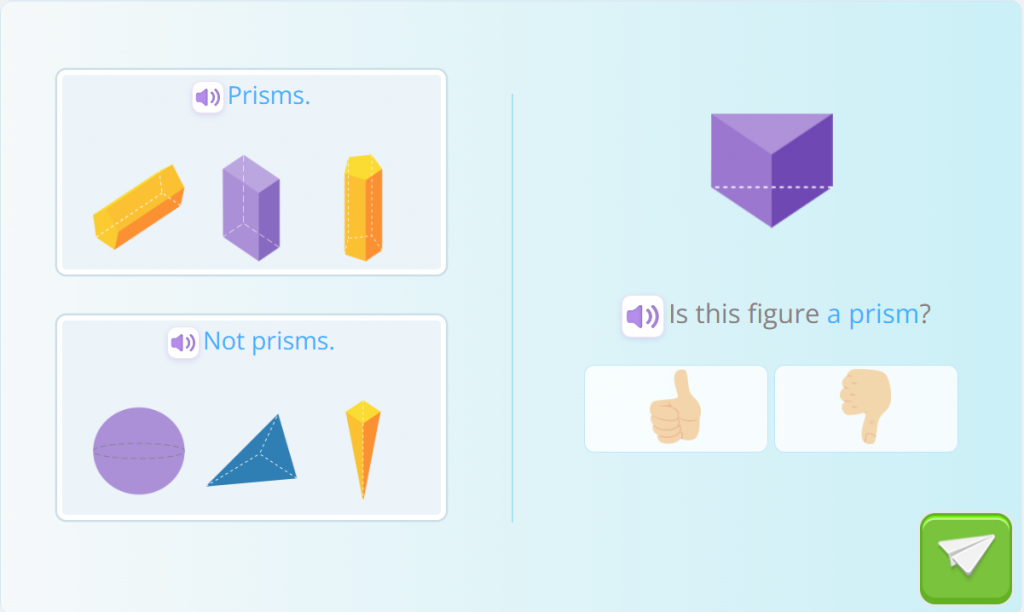
Before we dive into the fascinating world of these three-dimensional geometric figures, we are going to test your skills with an exercise. We’ll show you some figures and your task will be to determine whether they are prisms or not and then, figure out what is a prism. Get ready for the challenge!

The answer linked by @tmwilson26 is certainly helpful, but it may not be what you are looking for. There are a couple of different ways to approach this problem, and it depends a little bit on the equipment you have available. Note that if you have a zoom lens, leaving the iris at a fixed value will not, in general, result in a constant NA - instead the NA will depend on the focal length as well as the iris aperture.

Now you can repeat this measurement for different settings of the focal length of the zoom lens, and for different values of the iris setting. Note that by defocusing to various points and measuring the slope you avoid the problem of not knowing the focal length of the lens.

Working f-number

So if you plot the spot radius as a function of $\frac{f^2}{s-f}$ for different values of $s$ you should get a straight line whose slope is the tangent of the numerical aperture.

Prisms can be classified according to the number of sides of their bases. For example, if a prism has a triangular base, it is called a triangular prism. On the other hand, if it has a square base, it is known as a quadrangular prism. If the bases are parallelograms and the angles are right angles, it is called a rectangular prism. And remember, a prism is still a prism even if  “falls over” and its bases are not at the bottom and top of the figure. Check out these examples of prisms and their names!

You can find them in buildings, food packaging, toy boxes and many other places. We encourage you to look around and try to identify the prisms you find – don’t be surprised if you start seeing them everywhere!

$$\begin{align}d - f &= \frac{s\cdot f}{s - f} - f \\ &= \frac{s\cdot f}{s - f} - \frac{f(s-f)}{s-f}\\ &=\frac{f^2}{s-f}\end{align}$$

Numerical apertureofoptical fiber

Welcome to this post about prisms! Have you ever wondered what is a prism? Look no further! In this guide, we will explain everything you need to know about prisms.

A prism is a three-dimensional geometric figure that has two parallel and equal bases, which are polygons. These bases are joined by lateral faces that are also polygons. Prisms exist in various shapes and sizes, which makes them very interesting objects to learn about.

Na of lensformula

Assuming you know the focal length, and that you focused the lens on infinity (so you set $d' = f$), then your imaging plane would be away from the in-focus plane by a distance $d - f$. In the small angle approximation, the point would become a circle with a radius $r = NA\cdot (d-f)$.

Numerical apertureofmicroscope

Prisms are present in numerous everyday objects. Prisms are used in a variety of areas, from architecture to engineering. Architects can use prisms to design and construct impressive buildings, while engineers can use them to create strong and efficient structures.

Now that we have learned and reviewed a little more about what is a prism, we are ready to check the exercises from before!

Now we can use the formula for the distance to the focal point. If the source is a distance $s$ from the lens, and the focal length is $f$, then we expect the point to come into focus at a distance $d$ where

A simple setup would focus a point source of light onto a ground surface (a focusing screen) that is mounted on an optical rail (so you can move it along the optical axis). Once you have found the focal point, you move the surface a known distance away, and measure the size of the focal spot (I would recommend using an eyepiece graticule to make the measurement straightforward). Repeat this for a few different distances, and determine the slope of the straight line through the plot of spot radius vs distance to focal point. This slope represents the tangent of the half-angle of the iris subtended at the focal point.

NAobjectivelens

Numerical aperture formula

I have a lens system made up of some components of the Leica Z16 APO zoom system. This includes a built-in iris diaphragm to adjust the Numerical Aperture (NA) and therefore the depth-of-field (DOF).

With this guide on prisms and the challenge of identifying these figures, I hope you have enjoyed learning and are ready to delve even deeper into the study of these fascinating geometric figures. Check out Smartick to continue learning about prisms and many other topics.

To get the total area of the prism, think carefully about what a prism is and… you will certainly figure out how to calculate the area! A prism can be developed like this:

NA of lenscalculator

The iris is marked with some repeatable settings labelled 1-5. I can't find any documentation to tell me what the actual size of the iris is at these settings but I need to work out the NA at each one. Is there a simple way of doing this?

The comments that you write here are moderated and can be seen by other users. For private inquiries please write to [email protected]

When studying prisms, it is also important to know some additional terms. For example, the height of a prism is the perpendicular distance between the bases, and the edge is the segment that joins two consecutive vertices of one base with the corresponding vertices of the other base.

This does require you to know the focal length of the lens, and the lens to be focused on infinity. Measuring the distance to the optical center of the lens can be tricky - a zoom lens is a composite lens, and they don't always have an obvious "center". You can use the distance to the focal plane instead - that should be $s+f$ .

EDIT Since your lens is connected to a CMOS sensor, the above approach will not work for you. I recommend instead that you put a point source in front of the lens at a controlled (variable) distance, and measure once again the spot size.

To understand it better, imagine you are holding a rectangular box in your hands. This box is a concrete example of a prism. Its base is a rectangle, and the lateral faces are also rectangles. However, prisms can have bases in the form of triangles, squares and even more complex polygons.

We can simply calculate the area of the bases and the area of the lateral faces and then add it all up. But if you want, to know the exact formula, we have another post you can visit.

Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.