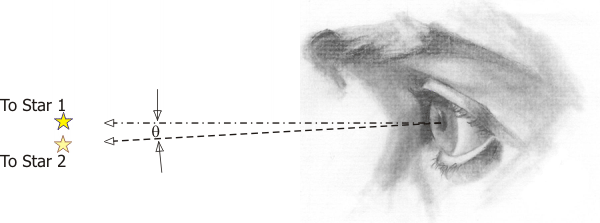
For that reason we measure distances and sizes in the scope image in terms of angles – degrees and fractions of degrees. The actual system is not degrees and decimal degrees, but instead it’s degrees, arc-minutes, and arc-seconds, which works just like hours, minutes & seconds. So there are

As the image gets magnified for the observer, the position of each feature in the image moves to a larger and larger angle off the centerline (i.e. the line looking straight ahead). Hence the magnification can be figured as the ratio of the angle seen at the eyepiece to the angle seen by the objective lens. For our analysis let's define some terms:

Wait a minute... the magnification is the focal length of the objective divided by the focal length of the eyepiece... so -- don't I need to tell you the focal length of the objective? Ah, but I have. Since the f-ratio is the focal length of the objective divided by the diameter of the objective, fR = fO/DO, then the focal length of the objective is found from

Calculating field of viewformula

Then the eyepiece, with a much shorter focal length, lets you get very close to that image to look at it, and -- surprise -- when you get closer, the image is bigger. If the eyepiece lets you get twice as close, the image is twice as big. If the eyepiece lets you get 50 times closer, then the image is 50 times as big. Simple.

Nikon specs their 10-24mm DX lens as having AoV of 109 degrees at 10 mm and 61 degrees at 24 mm when used on a DX camera. This does not agree with your table above. However, using their two numbers, you can easily calculate the sensor size from your formula–it is 28.4 mm. This is exactly the diagonal of the cropped sensor size of 23.5 x 15.7 mm.. Thus, Nikon uses the diagonal for quoting their specs, not the width of the sensor.

If you hold up your eyepiece by itself and look through it, assuming you don't go cross-eyed trying, you will see that there is an upside-down image. The width of that image, measured as an angle, is the field of view of the eyepiece. Typically, an eyepiece has a field of view of 50-60°, although there are wide-field eyepieces that go up to as much as 82° (and higher -- I just saw one that has a field of 100°!).

Notice, though, that based on the discussion above, different focal length eyepieces really are just moving you closer to, or further from, the image plane of the objective. When you get closer, the image is bigger (higher magnification) and when you get further, the image is smaller (lower magnification). This is a very effective (and very accurate) way of thinking about how the scope works.

My first telescope was a Meade 6600 -- they don't make it any more -- it's a 6-inch f/5 Newtonian scope. It came with a 25mm eyepiece. So... what was the magnification I was getting with this scope?

So I control how big the image looks simply by getting closer to or further from the image. Now let's see how the mathematics say exactly the same thing.

Thanx for the math. Can the view angle and/ or field of view for fish-eye lenses both rectilinear and circular image types also be calculated? It is my understanding the formulas are more complicated. I am interested because I have two fisheye Zuiko lenses from OM-2 & 4 cameras which I would like to use with adapter on Panasonic G 85 or Canon M 50. Can you help? TIA

As I continue to build out the photographic knowledge base on the site with articles like Understanding Neutral Density Filter Names and Numbers, and Understanding Aperture, I thought I’d write a quick post about how to calculate field of view for a photographic lens. Lenses are usually described by their focal length, expressed in mm, but how does this translate to field of view?

Thanks for the suggestion Kay. I like the idea, but there are many phone apps out there that offer this already, and they do a better job than I could ever do. I would suggest buying the app called “PhotoPills”, it has angle of view and depth of field calculators in it and it’s a great app for many things related to photography.

As well as calculating the angle of view, we can also use the same trigonometry to calculate the field of view as a linear measurement, as long as you know the distance to your subject, or, if you know the size of your subject and the focal length you are going to use, it could tell you how far away from it you need to be to get it to fill the frame. The units of measurement will be constant in the equation, so if you use metres as your distance to subject, the linear field of view will also be in metres.

I’ll be honest Michael, I don’t have time to do the math for you. The idea was to create a resource for people to calculate this themselves. All the equations you need are right here on the page. Just plug your numbers in 🙂

By submitting a comment this form also collects your name, email and IP address so that we can prevent spam. For more info check our privacy policy.

See? It's how far the objective is from the image compared to how close the eyepiece can get to it. You get closer and the image gets bigger.

Note: If your calculator is working in radians, you need the (180/π) part at the end. if your calculator is working in degrees, you do not need that bit! If you aren’t sure… it will become pretty obvious when you run the equation as results will be wildly wrong.

We can use the diagram above to find the magnification for this telescope. Light rays from a distant point arrive at the objective in parallel. The ray that passes through the center of the lens is important for the analysis, because that ray (unlike the others) is not bent and forms a straight line through the lens.

How to calculatefield of viewdiameter

What is the tiniest detail I can see at this magnification? We usually describe this in terms of how close two stars can be together and still tell them apart as two stars. We're also usually talking pretty darn close, so it is measured in arcseconds.

Once you understand the principle, the calculation is pretty easy. Don't underestimate the importance of being able to find this number, though, it is fundamental to the determination of most other performance parameters of the telescope.

Field of viewmicroscope Calculator

In the section on Maximum Magnification it's shown that a person with 20/20 vision can tell apart two stars that are as close as 120 arcseconds. So if you want to be able to see two stars that are much closer than that, the telescope will need to magnify them up to be 120 arcseconds apart. How close can they be if my magnification is M? What resolution, when magnified by M, will be 120 arcseconds?

The Minimum Magnification page explains how you can determine magnification from the exit pupil, and the Surface Brightness page explains why you would care about something like that.

The larger the field of view, the wider the lens is and the more of a scene you are going to see with your camera. Telephoto and super telephoto lenses have very small fields of view, just a few degrees, so they aren’t able to see very much of the scene in front of them, although the compensating virtue is that what they do see, is much larger in the frame. A wide angle lens for landscape photography has a very small focal length, and therefore a large field of view that lets you record broad landscapes in a single shot.

Then the angle of this incoming ray from the centerline, θO, is the same at the front and the back of the lens. Follow this line (the blue line) from the center of the objective to the focal point. The focal point, by definition, sits at distance fO from the objective, and we will postulate that this particular point sits at distance h above the centerline at the focal plane.

Your email address will not be published or shared. Comments that use abusive langugage, fake email addresses and fake names will be marked as spam. Please note that if you include a link in your comment, it will need to be moderated before it appears on the site. Required fields are marked*

As far as I can tell, it is correct. I just plugged some values into other online FOV calculators and the FOV calculator in the most popular photography iPhone app and all got the same answers that are in my table. 36mm is the width of a full frame sensor.

Notice above in the "small image" I can see more of the sky around Jupiter, and in the "big image", I can see less of the sky around it. The span — distance across the image from one side to the other — is bigger at low magnification and smaller at high magnification. We refer to this span as the "field of view". Let's figure out how big that actually is.

your FOV table is wrong. i think you took 36mm width instead of the diagonal. =2*ARCTAN(SQRT(24^2+36^2)/(2*”focallength”))*(180/PI())

Field of viewmicroscope 40x

Field of View. How many feet both horizontally and vertically in FOV using a 2000mm lens at 800 yards? I am trying to decide if I want to spend the money on a Nikon that comes with that lens.

Then if I am looking at two stars, the distance between them is expressed as an angle, in degrees, or in arc-minutes, or in arc-seconds. In the equations, we use θ (the Greek letter "theta") to represent angles.

When you expand the image by magnification, you can no longer see the whole field that you could see before magnification. So for example if you magnify the image by a factor of ten, you now can only see one-tenth of the field you had without magnification.

Dan, I’m a newbie to landscapes, and I’m not a professional. So, here’s a little feedback. Please understand that I don’t necessarily have the right language to ask the right questions. What I was really looking for is a way to know what general lens size to use to get a “how large a field of view. The math is helpful, but really not intuitive, especially if your last experience with higher math was 30+ years ago. What was a very useful visual for demonstrating angle of view is the first illustration you had, namely, the “topdown” view of the camera with cones coming forward in different colors. A visual chart or series of charts showing an object at say 200 yards, with the focal point in the center, and a second overlay on top of that showing how much distance to the front & back of the focal point remains in focus relative to the aperture would be ideal. I realize you are probably laughing out loud at this, & don’t have anywhere near enough time for a project of that size, & probably even less inclination to actually do it, but it would be enormously helpful, and a lot more visually intuitive. Thanks so much.

Everything in the night sky is so far away that it’s not the actual distances between things that we see, it’s the differences in the angle from our vantage point.

I need to shoot down on a square card table, 35 inches on each side (including margins) at a distance of about 1 meter. I am using a Panasonic G6 with the 14-42mm kit lens set at 14mm. Online calculators using the formula FOV (rectilinear) = 2 * arctan (frame size/(focal length * 2) indicate that the 14mm focal length should cover 35.14 inches in the vertical dimension at a distance of 41 inches. When I actually tried it, I had to be at least 11 feet back from the table. What gives?

fO = DO×f_R = 152.4 × 5 = 762 mm.

Then the magnification is f_O/f_e = 762/25 = 30.48, which we would just call 30.

The eyepiece has a field of view of 52°, so the field of view for the telescope at this magnification will be 52 ÷ 30 = 1.7°.

Then the image resolution at this magnification = 120/30 = 4 arcseconds. I would just be able to split a double star that is 4 arcseconds apart, like gamma Leonis.

Dependence on the Eyepiece

Since I got this scope, I've gotten a number of eyepieces so I can work at different magnifications. I have a 15 mm, a 9 mm, and a 4 mm eyepiece, in addition to the 25 mm. Let's see what these do for me in magnification and field of view, given the eyepieces each have a field of view of 52°:

Eyepiece	Arithmetic	Magnification	Field of View	Resolution
25 mm	762/25 =	30	1.7°	4 arcsec
15 mm	762/15 =	50	1.0°	2.4 arcsec
9 mm	762/9 =	85	0.6°	1.4 arcsec
4 mm	762/4 =	190	0.3°	0.6 arcsec

Later on, where we talk about minimum and maximum magnification, we examine this set of eyepieces and how well matched it is to this scope.

Dependence on the Scope

I also have a 90mm f/13.9 Meade ETX, which came with a 26mm eyepiece. What is the magnification on this much smaller scope?

Same arithmetic as above:

f_O = D_O×f_R = 90 × 13.9 = 1250 mm.

Then the magnification is f_O/f_e = 1250/26 = 48.

So the larger diameter scope, with a low f-ratio, has a much lower magnification than the small diameter scope, with a much bigger f-ratio. In general this will be the case -- high f-ratio tends to mean high magnification, and low f-ratio tends to mean low magnification. So why in the world would someone want a scope with a low f-ratio?

To understand the answer to that question, you need to dive into the discussion on Surface Brightness.

Back to Telescope Equations Home Page

Questions

Your questions and comments regarding this page are welcome. You can e-mail Randy Culp for inquiries, suggestions, new ideas or just to chat.
Updated 11 May 2019

We will also define the focal length of each lens, that is, the distance from the lens where it focuses light to a point.

Calculating field of view ofa microscope

This website may contain affiliate links. If you buy something through one of these links, we might make a small commission.

Now follow the red line from the focal plane to the center of the eyepiece and you can see that, likewise, the angle at the eyepiece, θe can be found as h/fe.

Since the equation for field of view contains the sensor width, which determines the crop factor of a sensor, this is another way to see the effect that the crop factor of a camera has on an image. The smaller the sensor, the larger the crop factor, and the smaller the field of view for a given focal length. Below I have included data for full frame field of view, as well as the three most common digital crop factors. If you want to learn more about crop factor, you can read my tutorial: How To Calculate a Camera’s Crop Factor.

Field of viewmicroscope 10X

So to find what the field of view will be in your telescope, first find the field of view of the eyepiece from its specifications, then divide by the magnification of your scope (with that eyepiece). Expressed as an equation this comes out to be

In theory, we could change the magnification either by changing the focal length of the objective lens or by changing that of the eyepiece. In reality, the objective is permanently mounted in the scope and we're not about to change it. To change magnification, we will change the eyepiece.

Calculating field of viewcalculator

When the stars are very close, it is common for us to measure their separation in terms of just a few arc-seconds, which is one 3600th of a degree. That works out to about one-fourth of one-thousanth of a degree!

I am not at all sure which is the best way to quote, but it is important to know how the quoted numbers are defined. Thanks for your very useful discussion.

The equation with distortion is quite a bit more complicated, so even apps like PhotoPills haven't modelled it. It has 4 variable coefficients and an additional SIN function. Here is a calculator which extends to lenses with distortion: https://commonlands.com/pages/fov-calculator

Incidentally, notice how I characterize the scope and the eyepiece... the scope by its diameter and f-ratio, the eyepiece by its focal length. This is common parlance. It's also common to call out the scope diameter in inches, but for our purposes we will need to convert to mm. So the value we want for DO is 6 × 25.4 = 152.4mm.

If you want to use the field of view equation on this page to calculate the field of view for a sensor size other than the four that have been provided, you’ll need to refer to use this list of common sensor sizes and their crop factor.

Calculating field of viewmicroscope Worksheet

If you read lens specifications (yes, I’m that kind of guy) on manufacturer’s websites, they’ll often quote the field of view (F.O.V) of a lens as well as the focal length. When they do this in photographic terms, they’re talking about horizontal field of view in degrees, and whilst any lens will also have both a vertical and a diagonal field of view, they are rarely talked about in relation to photographic lenses.

It must be noted here that Canon has actually used difference sensor sizes for their APS-C cameras over the years. Since the sensor dimension does affect the field of view, this should be taken into account in order to be 100% accurate. For the data table below I have chosen to use the sensor width of 22.5mm because this is the one that Canon seem to have stuck with for their own calculations, and it is also the dimension that gives exactly a 1.6x crop factor. Whilst they do have 22.3mm and 22.4mm sensor widths on the market as well, this minuscule difference would not actually make any noticeable difference to your images, but if you ran your own calculations for your own camera and found they did not match my numbers, this will be the cause of the difference. It was the source of some head scratching for me when I was figuring all this out myself!

I would check that your camera is in full output. If you use are using a smaller output resolution, your FoV will be cropped. The frame size input will be smaller.

In spite of all the diagrams and equations, what a telescope does to magnify the images is not magic or even complicated. It is actually quite simple and intuitive.

Note that this equation HSize/2=f*Tan(FoV/2) is inaccurate if your DSLR lens has >1% distortion. So, it shouldn’t be used for lenses like the Canon 11mm-22mm and most <15mm EFL 35mm-format type lenses. The G6 14mm has ~5% distortion.

The objective lens brings the image to a focus at its focal length. When viewed from the position of the objective lens, this image of the sky is the same size as the eye's view of the sky -- that is, distance angles between stars are exactly the same as you see them when you look up.