Laser safety - 10 milliwatt laser

 2024-10-25 10:00:21

Gaussian beam

Because they can be focused to the smallest spot size of all electromagnetic beams, Gaussian beams can deliver the highest resolution for imaging, as well as the highest power density for a fixed incident power, which can be important in fields such as material processing. These qualities are why lasers are such attractive light sources. To obtain the tightest possible focus, most commercial lasers are designed to operate in the lowest transverse mode, called the Gaussian beam.

Dear Yosuke, Is the background method applicable to the case of an interface? Suppose the beam is incident from air to glass, is this formular still valid? If not, how to implement the correct one? Thank you Best regards Simon

■ Characteristics ･ Display "Appropriate distance between eyes and lenses" on the aspherical lens body that can expand a wide area at a high magnif...

By providing your email address, you consent to receive emails from COMSOL AB and its affiliates about the COMSOL Blog, and agree that COMSOL may process your information according to its Privacy Policy. This consent may be withdrawn.

Dear Yasmien, Can you please go through our technical support, support@comsol.com? We need to see your model to solve your problem. Thank you. Yosuke

■ Characteristics ･ Loupe used between the eyelids ･ Lightweight, large caliber and easy to see ･ The frame has a hole without air, so the lens is ...

■ Characteristics ･ "Defractive lens" (multiple -time folding structural lens) filled with innovative technologies ･ Thin and stylish square design...

feature ■ 132mm diameter large aspherical lens ■ Bright vision with 85 LED lights ･ 2400-6000 Lux (3 steps of brightness) ･ There is no flicker, a...

Dear Yasmien, 1) You can not focus a beam to an infinitely small size. Yes, the number I gave you is lambda/pi. I have no proof for this but it is what I know as the smallest possible spot size for a wavelength no matter what your particle size is. The wavelength is not the determining factor of w0. The minimum beam waist radius is determined by how the laser beam has originally been generated inside a laser cavity. You can’t change it. You can focus the beam by a focusing lens but you can only worsen it or at most you can keep it as it is depending on the lens quality. So when you simulate a focusing laser beam, you should have the specification of the laser beam. 2) I gave w0 = 10 lambda. If your wavelength is 400 nm, 10×400 nm = 4 um is the waist radius for which the paraxial Gaussian beam is a good approximation. For 500 nm, it’d be 5 um. Best regards, Yosuke

■ Characteristics ･ Eschenbach's long seller ･ You can select the shape, color, size, and magnification of the case ･ Bi -complex lens that can be ...

This factorization is reasonable for a wave in a laser cavity propagating along the optical axis. The next assumption is that |\partial^2 A/ \partial x^2| \ll |2k \partial A/\partial x|, which means that the envelope of the propagating wave is slow along the optical axis, and |\partial^2 A/ \partial x^2| \ll |\partial^2 A/ \partial y^2|, which means that the variation of the wave in the optical axis is slower than that in the transverse axis. These assumptions derive an approximation to the Helmholtz equation, which is called the paraxial Helmholtz equation, i.e.,

Hi, I am rather new to Comsol. Thanks for this good explanation of Gaussian beam. I have a question: What should I change/add to incident a Gaussian beam at interface with some degree of angle if the scattered field formulation is chosen (as you have shown in window above)?

■ Characteristics ･ Lavision -based eyeglass type loupe by its own circular configuration precision plastic lens ･ Even if the magnification increa...

Plots showing the electric field norm of paraxial Gaussian beams with different waist radii. Note that the variable name for the background field is ewfd.Ebz.

Thanks Yosuke, Could you please guide me how I can write an expression for a gaussian beam (in 2D) propagating in x-direction while the polarization in y-direction? And, also how I can define a coordinate transfer in expression for an incident angle of the beam?

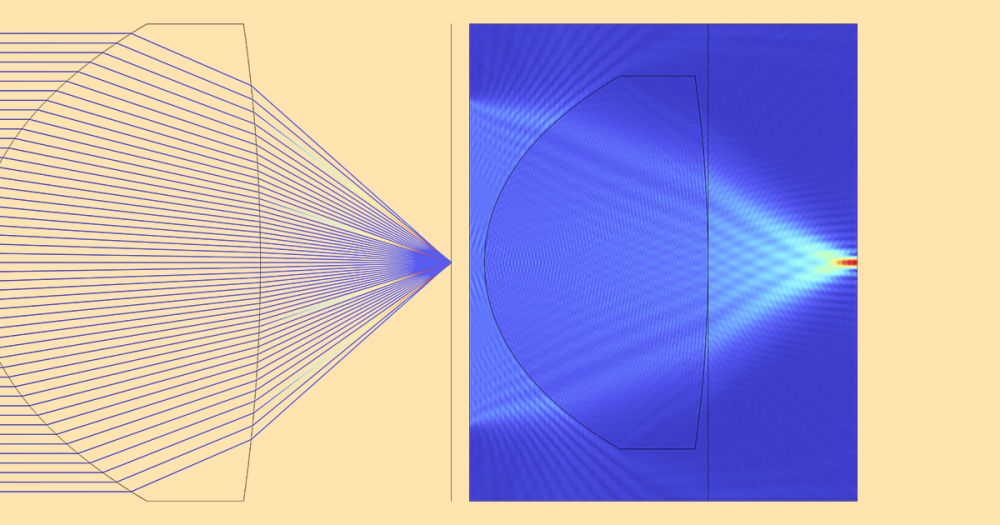
The paraxial Gaussian beam formula is an approximation to the Helmholtz equation derived from Maxwell’s equations. This is the first important element to note, while the other portions of our discussion will focus on how the formula is derived and what types of assumptions are made from it.

■ Characteristics ･ Case with excellent strength and airtightness ･ Case material: Glass fiber processing enhancement plastic

Dear Jana, Thank you for reading this blog. There are some limitations for the built-in Gaussian beam feature. 1. You can only propagate it along the x or y or z axis. Due to this limitation, you will have to rotate your material in order to simulate a beam at an angle. 2. The focus position needs to be known a priori. This is a little bit tricky to explain but you need to know the focus position inside your material and enter the position in “Focal plane along the axis” section because COMSOL won’t automatically calculate the focus position shift if you only know the field outside your material. Because of the convergence of a Gaussian beam, there will be a refraction at a material interface, which causes the focus shift. For more details about the Gaussian beam focus shift at interfaces, please refer to this paper: Shojiro Nemoto, Applied Optics, Vol. 27, No. 9 (1988). If you would like a more flexible way, you can define a paraxial Gaussian beam in Definition and also define a coordinate transfer. Please send support@comsol.com a question on this method since it’s a little bit difficult to explain here. Best regards, Yosuke

As such, it would be reasonable to want to simulate a Gaussian beam with the smallest spot size. There is a formula that predicts real Gaussian beams in experiments very well and is convenient to apply in simulation studies. However, there is a limitation attributed to using this formula. The limitation appears when you are trying to describe a Gaussian beam with a spot size near its wavelength. In other words, the formula becomes less accurate when trying to observe the most beneficial feature of the Gaussian beam in simulation. In a future blog post, we will discuss ways to simulate Gaussian beams more accurately; for the remainder of this post, we will focus exclusively on the paraxial Gaussian beam.

■ Characteristics ･ Stand type that is focused just by looking into the lens while placed ･ High magnification loupe that is also used for checking...

Editor’s note, 7/2/18: The follow-up blog post, “The Nonparaxial Gaussian Beam Formula for Simulating Wave Optics”, is now live.

Gaussian beampropagation lightmachinery

The above equation is the scattered field formulation, where COMSOL Multiphysics solves for the scattered field. This formulation can be viewed as a scattering problem with a scattering potential, which appears in the right-hand side. It is easy to understand that the scattered field will be zero if the background field satisfies the Helmholtz equation (under an approximate Sommerfeld radiation condition, such as an absorbing boundary condition) because the right-hand side is zero, aside from the numerical errors. If the background field doesn’t satisfy the Helmholtz equation, the right-hand side may leave some nonzero value, in which case the scattered field may be nonzero. This field can be regarded as an error of the background field. In other words, under certain conditions, you can qualify and quantify exactly how and by how much your background field satisfies the Helmholtz equation. Let’s now take a look at the scattered field for the example shown in the previous simulations.

Dear Yosuke Mizuyama Very interested topic. I have one question, please. Why lambda is equal to 500nm and used in COMSOL as the default value for the calculation of frequency (f=c_const/500[nm])?

■ Characteristics ･ Base -in prism to reduce congestion burden due to an increase in positive degree ･ Stylish design ･ High fit with spring hinge

Grossmann Uhren GmbH was established in 2008 and is a German watch manufacturer based in Glashütte, Saxony. The company specializes in high-end, hand-crafted mechanical watches, with collection lines Benu, Tefnut, and Hamatic. These watches have special materials like silver, steel, gold, and enamel, as well as features like engraved parts, balance adjustments, and extra functions like power level and date. The company produces watches in small batches and often in limited editions. It also allows its clients to create a personal Moritz Grossmann watch by choosing from a diverse selection of clasp types and bracelet lengths.

This section provides an overview for magnifying glasses as well as their applications and principles. Also, please take a look at the list of 19 magnifying glass manufacturers and their company rankings. Here are the top-ranked magnifying glass companies as of November, 2024: 1.Shinwa Rules Co., Ltd., 2.Grossmann Uhren GmbH, 3.Gilson Company, Inc..

Dear Yasmien, Thank you very much for reading my blog and for your interest. Do you have to focus your beam to the size of the nano-particle? The beam waist size is determined depending on how much you have to focus. For that wavelength range, the least possible waist radii are as large as 127 nm to 159 nm, though. And for these numbers, the paraxial formula will not give you an accurate result. If a slow (gently focusing) beam works for your characterization, the waist radius of 4 um or larger would work and our Gaussian beam background feature gives you a correct result.

Deluxe Scientific Surgico Pvt Ltd., established in 1996 and based in New, Delhi, India is a manufacturer and supplier of medical, scientific and hospital equipment. The company’s product portfolio includes anesthesia products, autoclaves and sterilizers, autopsy products, hospital furniture, and more. These products cater to medical and scientific institutions including hospitals, research centers, learning institutions, and more. The company’s products are ISO 9001:2008 and ISO 13485:2003 certified and comply with CE Standards. Deluxe Scientific has a worldwide network of distributors, serving clients in the medical and scientific industries in over 90 countries worldwide.

■ Characteristics ･ Colored aberration correction high -quality aberration lens (acromart) ･ With monopic adjustment function ･ Enlarged image that...

Computer Network Accessories Inc., based in Dayton, Ohio, is an online supplier of several electronic products, such as power adapters, network hardware, and bulk cabling. The company also stocks computer hardware and accessories like keyboards, hard drives, and modems and sells toner cartridges compatible with several brands like HP, IBM, and Epson. The company has an online catalog of its products where customers can make orders, and it allows purchase orders. It provides free shipping for all orders over $99, and customers can return goods if unsatisfied within 30 days of purchase.

The primary mechanism of a magnifying glass involves convex or Fresnel lenses. Convex lenses focus light to a point, creating an enlarged virtual image of an object placed within the focal length. Fresnel lenses, on the other hand, offer a thinner, lightweight alternative, albeit with some compromise in image quality due to diffraction.

Dear Yosuke Mizuyama Very interested topic. I have one question, please. Why lambda is equal to 500nm and used in COMSOL as the default value for the calculation of frequency (f=c_const/500[nm])?

Dear Yasmien, That means there is no purely linearly polarized beam for non-paraxial Gaussian beams. There is a reference in the pdf document for the nanorods model, M. Lax, W.H. Louisell, and W. B. McKnight, “From Maxwell to paraxial wave optics”, Physical Review A, vol. 11, no. 4, pp. 1365-1370 (1975). You don’t want to simulate what really doesn’t exist, do you? If your beam is really a tightly focused beam, it has a propagation component inevitably. So you have to add it no matter how it’s a different component than your preferred plane to which you want to believe it’s polarized. Best regards, Yosuke

The following plot is the result of the calculation as a function of x normalized by the wavelength. (You can type it in the plot settings by using the derivative operand like d(d(A,x),x) and d(A,x), and so on.) We can see that the paraxiality condition breaks down as the waist size gets close to the wavelength. This plot indicates that the beam envelope is no longer a slowly varying one around the focus as the beam becomes fast. A different approach for seeing the same trend is shown in our Suggested Reading section.

Plots showing the electric field norm of the scattered field. Note that the variable name for the scattered field is ewfd.relEz. Also note that the numerical error is contained in this error field as well as the formula’s error.

Hoffmann SE is a supplier and distributor of quality tools, workshop equipment, and personal protective equipment that was established in 1919 and is based in Munich, Germany. The company’s product portfolio includes hand tools, power tools, measuring tools, clamping tools, cutting tools. The performance, excellence, and dependability of the tools, workshop equipment, and personal protective equipment have been carefully considered. The products are utilized in various industries, including metalworking, automotive, aerospace, jewelry, and electronics. Additionally, it is designed with energy efficiency and environmental compliance in mind.

■ Characteristics ･ Special design that is easy to sit on a desk and look into it ･ It is hard to get scratched, bright and bright

The paraxial Gaussian beam option will be available if the scattered field formulation is chosen, as illustrated in the screenshot below. By using this feature, you can use the paraxial Gaussian beam formula in COMSOL Multiphysics without having to type out the relatively complicated formula. Instead, you simply need to specify the waist radius, focus position, polarization, and the wave number.

■ Glasses type work loupe ･ Focal length: around 40cm ･ Work distance can be obtained and work is easy ■ With the left and right independent visua...

Dear Daniel, Thank you for reading this blog. When we assumed time-harmonic waves to derive the Helmholtz equation from the time-dependent wave equation, we factored out exp(i*omega*t). Remembering this process, we get a time-dependent wave by putting the factor back, i.e., by replacing exp(-ik*x) with exp(i*(omega*t -k*x)) in the formula in this blog. This is implemented in second_harmonic_generation.mph in our Application Libraries under Wave Optics Module > Nonlinear Optics. I hope this helps! Best regards, Yosuke

Thanks Yosuke for such an interesting and clear post. The model I am currently working on includes a Gaussian beam focused by a high NA objective lens. Clearly, this is too tightly focused for the paraxial approximation to hold, and I encountered the problems you have described above. However, searching around the web I wasn’t able to find out so far anyone coming up with a workaround to these limitations. More in general, is there a way to simulate in COMSOL the point spread function of a high NA lens? You can imagine I am now really looking forward to the follow-up post you promised describing the solutions! I am wondering, are you planning to publish this any soon? Would you be able meanwhile to point to me some useful information on this matter? With kind regards, Attilio

■ Characteristics ･ Eschenbach's long seller ･ You can select the shape, color, size, and magnification of the case ･ Bi -complex lens that can be ...

2) When you write that 4 um is the proper w0, Do you mean that I can use this value for the whole previous wavelength spectrum? I mean is it constant?

Dear Yasmien, The solution is one of the valid methods for both 3D and 2D. Mesh refinement works for increasing the accuracy of finite element solutions. If you use a loosely focused Gaussian beam, yes, your paraxial Gaussian beam in your finite element model will become closer to the closed-form paraxial Gaussian beam. But if you use a very small waist size in the paraxial Gaussian beam formula, mesh refinement will not work to improve the error coming from the paraxial approximation. It doesn’t change the scalar paraxial approximation nature. The technique used in the model you referred to is actually a remedy to the fact that the Gaussian beam starts to show its vectorial nature when it’s tightly focused, which is negligibly small when the focusing is not tight where the scalar paraxial Gaussian beam formula is valid.

■ Characteristics ･ Bi -complex lens that can be enlarged from both sides of the lens ･ It is hard to get scratched, bright and bright ･ Wide visio...

Magnifying glasses today are not limited to traditional handheld models but also include eyeglass-type magnifiers for hands-free use. The advent of plastic lenses has made magnifying glasses lighter and more durable. As objects of interest become increasingly smaller, magnifying glasses have become indispensable tools for individuals across various professions and hobbies.

Opticolite India was established in 2005 and is a manufacturer and exporter of a range of telescopes and microscopes headquartered in New Delhi, India. The company’s main product line consists of magnifiers, bug viewers, telescopes, microscopes, and other optical instruments. It also offers paper binoculars, virtual reality glasses, plastic lenses, acrylic blocks, plastic torches, and peak loupes. The company is a major supplier of educational goods to schools and universities in India. It is certified to CE and ISO 9001 standards, IndiaMART TrustSEAL-verified, and serves markets across the UK, Australia, USA, and Europe.

Thanks for your clarification and I got the idea in using mesh. The explanation of the reason of existence an electric field component in the propagation direction is still unclear to me, I am sorry I did not understand it well. Also, why do we represent this component by differentiating the gaussian beam field according to the polarization direction?

Dear Yosuke, Thanks for your kind reply, it is very helpful, and yes I want to focus the beam to the size of the nano-particle with 6 nm radius, but I have 2 questions if you kindly allow: 1) I realized that you determine the waist radii depending on the wavelength only, Do you divide it by (pi)?, ignoring the particle radius. The second part of my question is should I depend on one factor only in determining w0 that is wavelength only? 2) When you write that 4 um is the proper w0, Do you mean that I can use this value for the whole previous wavelength spectrum? I mean is it constant? Best regards

{ Error in user-defined function. – Function: dE_dE__z__internalArgument Failed to evaluate variable. – Variable: comp1.emw.Ebx – Defined as: exp(i*phase)*(!(comp1.isScalingSystemDomain)*(comp1.es.Ex+((j*d((unit_V_cf*E(x/unit_m_cf,y/unit_m_cf,z/unit_m_cf))/unit_m_cf,z))/comp1.emw.k0))) Failed to evaluate expression. – Expression: comp1.emw.Ebx Failed to evaluate operator. – Operator: mean – Geometry: geom1 }

One of the COMSOL modes named “Nanorods” with application library path: Wave_Optics_Module/Optical_Scattering/ nanorods. In the “Model Definition” section at page 1 of this model, the author determined that the rods have dimensions less than wavelength, as my case, and as I understand he overcame the problem of Gaussian beam is an approximation solution by the following sentence and I will write it as it was reminded ” For tightly focused beams you also need to include an electric field component in the propagation direction”.

■ Characteristics ･ LED light light is evenly irradiated ･ Aspherical lens with little distortion ･ It is hard to get scratched, bright and bright ...

Gaussian beamsoftware

You can imagine I am now really looking forward to the follow-up post you promised describing the solutions! I am wondering, are you planning to publish this any soon? Would you be able meanwhile to point to me some useful information on this matter?

The original idea of the paraxial Gaussian beam starts with approximating the scalar Helmholtz equation by factoring out the propagating factor and leaving the slowly varying function, i.e., E_z(x,y) = A(x,y)e^{-ikx}, where the propagation axis is in x and A(x,y) is the slowly varying function. This will yield an identity

Traceable was established in 1978 and is headquartered in Webster, Texas, US, as a manufacturer and designer of serialized, calibrated, and certified Traceable lab instruments. The product portfolio includes thermometers, barometers, hygrometers, manometers, controllers, timers, clocks, stopwatches, and lab tools. These products find applications in diverse fields, serving purposes such as temperature and atmospheric pressure measurement, humidity monitoring, pressure measurements, process control, timekeeping, and laboratory analysis. These products are utilized across various industries, including healthcare, laboratory, and industrial sectors, as well as in biopharmaceutical industries.

When I write an expession for x2, as you mentioned above, it shows Syntax error in expression – Expression: x*cos(theta) – y*sin(theta) – Subexpression: – y*sin(the – Position: 14 Error in automatic sequence generation.

■ Characteristics ･ Universal design that is hard to get tired even when used for a long time in a natural form that is easy to grasp ･ Expanding c...

■ Characteristics ･ Variable magnification is variable while left -5 steps adjustment from 2.2 times to 3.4 times ･ Approximately enlarged image th...

Lasercalculator

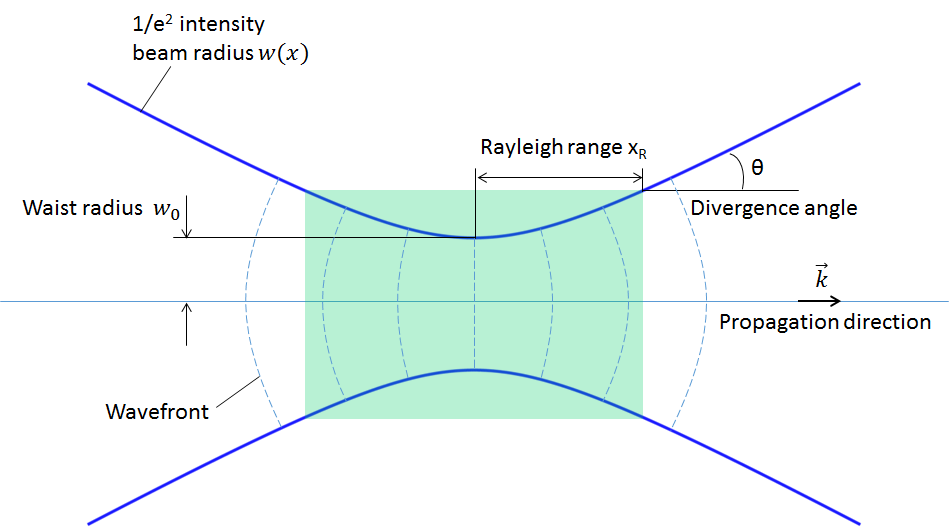
Note: It is important to be clear about which quantities are given and which ones are being calculated. To specify a paraxial Gaussian beam, either the waist radius w_0 or the far-field divergence angle \theta must be given. These two quantities are dependent on each other through the approximate divergence angle equation. All other quantities and functions are derived from and defined by these quantities.

■ Characteristics ･ Bi -complex lens that can be enlarged from both sides of the lens ･ It is hard to get scratched, bright and bright ･ The grip w...

■ Characteristics ･ Expand letters up and down ･ Incorporated red line that is convenient for reading ･ It is hard to get scratched, bright and bri...

■ Characteristics ･ 420, 1421, 1424: Brightly expanded with the design that gathers light ･ 1421, 1424: Easy to hold and with a black frame to prot...

■ Features -The ball joint can freely adjust the position and angle of the lens. ■ Use ･ For precision tests such as boards.

For a rotated one at an angle theta, please replace x and y in the above expression with x2 and y2 and define x2 = x*cos(theta) – y*sin(theta) y2 = x*sin(theta) + x*cos(theta)

Dear Attilio, Thank you for reading my blog post and for your comment. We will publish a follow-up blog post with rigorous solutions in a few months. In the meantime, you may want to check out this reference: P. Varga et al., “The Gaussian wave solution of Maxwell’s equations and the validity of scalar wave approximation”, Optics Communications, 152 (1998) 108-118. In this paper, the authors give an exact formula for a nonparaxial Gaussian wave. Best regards, Yosuke

■ Characteristics ･ The case is an airtight structure that is hard to get dust ･ Compact size ･ Bi -complex lens that can be enlarged from both sid...

Dear Jana, Here’s the expression: Ex = 0 Ey = sqrt(w0/w(x))*exp(-y^2/w(x)^2)*exp(-i*k*x-i*k*y^2/(2*R(x))-eta(x)) Ez = 0 w0 = given waist radius, k = 2*pi/lambda w(x) = w0*sqrt(1+(x/xR)^2) xR = pi*w0^2/lambda R(x) = x+xR^2/x eta(x) = atan(x/xR)/2 For a rotated one at an angle theta, please replace x and y in the above expression with x2 and y2 and define x2 = x*cos(theta) – y*sin(theta) y2 = x*sin(theta) + x*cos(theta) Best regards, Yosuke

Dear Jana, That was a typo. Correct: y2 = x*sin(theta)+y*cos(theta) Other than that, if you have more questions on this particular one, please send your question to support@comsol.com with your model. That’d be more effective. Best regards, Yosuke

Hoffmann, Inc. is a manufacturer of reinforced concrete silos and chimneys, established in 1914 and based in Muscatine, Iowa. The company's range of products includes dry distillers grain, limestone, carbon steel, brick liners, and glass blocks. The reinforced concrete silos and chimneys offer durability, corrosion resistance, and structural stability, making them suitable for long-term storage and industrial applications. The products manufactured by Hoffmann, Inc. are primarily used in the storage and handling of materials in industries such as agriculture, construction, food processing, and chemical manufacturing.

Dear Yosuke, Thank you for this clear and informative demonstration of the paraxial beam functionality in COMSOL! At the moment I am working on in bulk laser material processing of sapphire where I need to define an Gaussian beam entering the material and focusing in the bulk. Since this process is time dependent ( we want to study the behavior ), I am looking for a time dependent description of the Gaussian beam to take into account the varying pulse energy. I noticed that the Gaussian beam is only available in the frequency domain, what do I need to know and model to study this in a time dependent study? Daniel

Dear Yosuke, Thanks for your clarification and I got the idea in using mesh. The explanation of the reason of existence an electric field component in the propagation direction is still unclear to me, I am sorry I did not understand it well. Also, why do we represent this component by differentiating the gaussian beam field according to the polarization direction? Could you recommend a source for reading?

･ The case is an airtight structure that is hard to get dust ･ Compact size, hanging on the neck through straps ･ It is hard to get scratched, brig...

Gaussian beamq parameter

Away from the previous question, do you think that decreasing the mesh size would increase the accuracy of gaussian beams in small structures?

Seedburo Equipment Company is a manufacturer and distributor of agricultural equipment since 1912 in Illinois. The company designs handling, testing, and grading equipment for grain, feed and seed industries and various agricultural processes such as Dividers, Moisture Testers, Grain Inspection, and Grading equipment, and seed counting and analysis equipment. There are also scales and balances, hemp and coffee equipment, Sieve Shakers, Test Sieves, and Screens amongst others that collectively serve the Agribusiness Industries.

In the scattered field formulation, the total field E_{\rm total} is linearly decomposed into the background field E_{\rm bg} and the scattered field E_{\rm sc} as E_{\rm total} = E_{\rm bg} + E_{\rm sc}. Since the total field must satisfy the Helmholtz equation, it follows that (\nabla^2 + k^2 )E_{\rm total} = 0, where \nabla^2 is the Laplace operator. This is the full field formulation, where COMSOL Multiphysics solves for the total field. On the other hand, this formulation can be rewritten in the form of an inhomogeneous Helmholtz equation as

Note: The term “Gaussian beam” can sometimes be used to describe a beam with a “Gaussian profile” or “Gaussian distribution”. When we use the term “Gaussian beam” here, it always means a “focusing” or “propagating” Gaussian beam, which includes the amplitude and the phase.

Dear Yosuke Mizuyama： Thanks Yosuke for such an interesting and clear post.My current work is a single crystal fiber laser, and I encountered the problem you described above while simulating the propagation of light in the pump!I am here to ask you what method can I use to simulate the propagation of a Gaussian beam (W0 =0.147mm) in a rod with a diameter of 1mm and display the light intensity distribution!I used the ray tracing module, but the results are too poor. Can you tell me how to implement my simulation?Thank you very much!

A bicon bex lens that can be enlarged from both sides of the lens. ■ Characteristics ･ High transparency, bright and bright ･ Transparent forever ...

Magnifying glasses are instrumental across various fields, aiding in reading, inspection, medical examination, jewelry appraisal, and precision work. They're particularly beneficial for individuals with low vision, offering enhanced visibility for everyday tasks and specialized work.

■ Characteristics ･ Cut the aberration of two -piece lens (the distortion of the enlarged image) of the two -piece configuration lens ･ The grip is...

■ Characteristics ･ The stand is made of mat chrome finished metal ･ It becomes smaller when folded and convenient to carry ･ Stand type that focus...

Spot size

In the above plot, we saw the relationship between the waist size and the accuracy of the paraxial approximation. Now we can check the assumptions that were discussed earlier. One of the assumptions to derive the paraxial Helmholtz equation is that the envelope function varies relatively slowly in the propagation axis, i.e., |\partial^2 A/ \partial x^2| \ll |2k \partial A/\partial x|. Let’s check this condition on the x-axis. To that end, we can calculate a quantity representing the paraxiality. As the paraxial Helmholtz equation is a complex equation, let’s take a look at the real part of this quantity, {\rm abs} \left ( {\rm real} \left ( (\partial^2 A/ \partial x^2) / (2ik \partial A/\partial x) \right ) \right ).

■ Characteristics ･ 2 lens configuration that keeps the distortion (apranate, acromart) ･ Case with excellent strength and airtightness ･ High qual...

The results shown above clearly indicate that the paraxial Gaussian beam formula starts failing to be consistent with the Helmholtz equation as it’s focused more tightly. Quantitatively, the plot below may illustrate the trend more clearly. Here, the relative L2 error is defined by \left ( \int_\Omega |E_{\rm sc}|^2dxdy / \int_\Omega |E_{\rm bg}|^2dxdy \right )^{0.5}, where \Omega stands for the computational domain, which is compared to the mesh size. As this plot suggests, we can’t expect that the paraxial Gaussian beam formula for spot sizes near or smaller than the wavelength is representative of what really happens in experiments or the behavior of real electromagnetic Gaussian beams. In the settings of the paraxial Gaussian beam formula in COMSOL Multiphysics, the default waist radius is ten times the wavelength, which is safe enough to be consistent with the Helmholtz equation. It is, however, not a “cut-off” number, as the approximation assumption is continuous. It’s up to you to decide when you need to be cautious in your use of this approximate formula.

This is the version of our website addressed to speakers of English in the United States. If you are a resident of another country, please select the appropriate version of Metoree for your country in the drop-down menu.

■ Characteristics ･ Loupe with a high magnification light that focuses on in the place ･ Set product of head and light grip (can be purchased by si...

And I wrote the component of electric field in propagation direction as following: (j*d(E(x,y,z),z)/emw.k0) where (z) is the polarization direction and I used it to overcome the paraxial approximation problem if you rememer, but I get this error:

Dear Yosuke, I read your kind answer carefully and understood it. I am really thankful to this discussion with you because I do learn from it, so excuse me in this extra question; One of the COMSOL modes named “Nanorods” with application library path: Wave_Optics_Module/Optical_Scattering/ nanorods. In the “Model Definition” section at page 1 of this model, the author determined that the rods have dimensions less than wavelength, as my case, and as I understand he overcame the problem of Gaussian beam is an approximation solution by the following sentence and I will write it as it was reminded ” For tightly focused beams you also need to include an electric field component in the propagation direction”. My question: is this solution appropriate in 3D or in 2D structures only? Away from the previous question, do you think that decreasing the mesh size would increase the accuracy of gaussian beams in small structures? I will wait your kind answer and really thank you in advance.

Carson Optical, Inc., founded in 1990, is an optical product manufacturer and supplier headquartered in Ronkonkoma, New York, United States. The company features a prototyping and optical metrology laboratory which complements product manufacturing protected by over 100 patents. These products include magnifiers and magnifying glasses, ranging from handheld and loupe to portable options. The company also offers a series of binoculars with high magnification and broad visibility across various lighting conditions. It further provides a range of biological, digital, and pocket microscopes. The company serves a global clientele, including the United Kingdom, Europe, and Asia, facilitated by international distribution centers.

Could you tell me the proper choice for the value of w0 and how can I use the gaussian beam formula as a background source in my case.

Shinwa Rules Co. was founded in Niigata, Japan, in 1971. Shinwa Rules Co. develops a variety of measuring products including calipers, thermometers, hygrometers, laser optical apparatuses, and sheet heating elements. Above these, Shinwa develops metallic rulers and squares. Additionally, Shinwa operates as an OEM supplier for special calibrations and machine tools, special surface fabrication, and etching on metallic parts.

■ Characteristics ･ Handy -loupe entry model that can be used regardless of age or gender ･ Case of recycling leather with vivid colors ･ It is har...

E-Tay Industrial Co. Ltd. has been a developer and manufacturer of optical lenses, magnifiers, and magnifying glasses since 1980 and is headquartered in Taipei, Taiwan. The company offers a wide array of optical products, including LED lighted magnifiers, optical lenses, and hand-held and hands-free magnifiers. It also produces children's binoculars, 3D glasses, solar eclipse glasses, and PIR sensor lenses for motion detection. The company provides OEM and ODM product development to meet the special needs of clients. It is certified by ÜV Rheinland and Dun & Bradstreet, serving the healthcare, education, and manufacturing sectors.

The special solution to this paraxial Helmholtz equation gives the paraxial Gaussian beam formula. For a given waist radius w_0 at the focus point, the slowly varying function is given by

Today’s blog post has covered the fundamentals related to the paraxial Gaussian beam formula. Understanding how to effectively utilize this useful formulation requires knowledge of its limitation as well as how to determine its accuracy, both of which are elements that we have highlighted here.

■ Characteristics ･ Linen tester's economy line ･ 1mm scale is engraved in the lower frame ･ It is hard to get scratched, bright and bright

A magnifying glass is an optical device designed to enlarge the appearance of objects through one or more lenses. Traditionally used to observe small details, magnifying glasses have evolved from simple glass lenses to include modern plastic lenses, enhancing their utility and accessibility.

Dear Simon, Thank you for your interest in my blog. The above formula is written for beams in vacua or air for simplicity. But the formula still holds if you read k as the wave number in a material, that is, if you use n*k instead of k, where n is the refractive index of the material. In COMSOL, the Gaussian beam settings in the background field feature in the Wave Optics module are set for the vacuum by default, i.e., the wave number is set to be “ewfd.k0”. But you can change it to “ewfd.k” for more general cases. COMSOL will automatically take care of the local “k” depending on where you have different materials in your domain. There is a tricky thing you have to keep in mind in this situation: You have to know the waist position wherever it is positioned. If a Gaussian beam is incident from air to glass and makes a focus in the glass, the waist position will be different from the case where the material doesn’t exist (See Applied Optics, Vol. 27, No. 9, p.1834-1839 (1988) ). You have to calculate the focus position first, and then enter the focus position in COMSOL. Best regards, Yosuke

■ Characteristics ･ 3 times with a large lens of 75 x 100mm (12dpt) ･ Enlarged image with little distortion to every corner of the lens -a two -pie...

■ Characteristics ･ Pendant loop with 8 crystal glass ･ You can pinch the Vatican and use it without touching the lens ･ It can be replaced with yo...

As you know the gaussian beam source that I asked you about I used it in 3D structure and was represented in my model by analytic functon with the next formula: E(x,y,z)= E0*w0/w(x)*exp(-(y^2+z^2)/w(x)^2)*exp(-i*(k*x-eta(x)+k*(y^2+z^2)/(2*R(x))))

Here, x_R is referred to as the Rayleigh range. Outside of the Rayleigh range, the Gaussian beam size becomes proportional to the distance from the focal point and the 1/e^2 intensity position diverges at an approximate divergence angle of \theta = \lambda/(\pi w_0).

I read your kind answer carefully and understood it. I am really thankful to this discussion with you because I do learn from it, so excuse me in this extra question;

■ Features ･ Cordless type light loupe using LED with long life. ･ AA batteries x 4 bottles, continuous lighting for 8 hours. ･ It can be used with...

Narang Medical Limited, established in Delhi, in 1989 is a manufacturer of medical Equipment, Hospital Furniture, Orthopedic Implants, and Instruments. Their product portfolio includes infusion pumps, anesthesia machines, defibrillators, and diagnostic devices used in various medical settings. The company products find application in Hospitals and Medical Centers, Clinics and Healthcare Facilities, Orthopedic Centers and Hospitals, and Ambulatory Surgical Centers. The company exports its products to over 80 countries including the USA and the Middle East.

■ Characteristics ･ Hang from the neck with the attached string and fix the lens to the chest. ･ Easy to see with large lenses ･ Recommended for ho...

Dear Yosuke, Thank you so much for this reliable blog. I have a question about one of limitations of paraxial gaussian beam. I am trying to study the optical characteristics of gold nano-particle (radius = 6nm) on a wavelength spectrum extended from 400 nm to 500 nm, and I do not know how I can determine the beam radius waist (w0) value. I think it will be less than wavelength and this will not match with the paraxial approximation for Maxwell equation that used in the suggested gaussian beam in your blog. Could you tell me the proper choice for the value of w0 and how can I use the gaussian beam formula as a background source in my case. Thanks in advance

Laguerre Gaussbeam

In COMSOL Multiphysics, the paraxial Gaussian beam formula is included as a built-in background field in the Electromagnetic Waves, Frequency Domain interface in the RF and Wave Optics modules. The interface features a formulation option for solving electromagnetic scattering problems, which are the Full field and the Scattered field formulations.

I am trying to study the optical characteristics of gold nano-particle (radius = 6nm) on a wavelength spectrum extended from 400 nm to 500 nm, and I do not know how I can determine the beam radius waist (w0) value. I think it will be less than wavelength and this will not match with the paraxial approximation for Maxwell equation that used in the suggested gaussian beam in your blog.

Gilson Company, Inc. is an American manufacturer and supplier of construction material testing equipment based in Lewis Center, Ohio. The company was established in 1939 with a primary focus on manufacturing the testing screen, a laboratory-scale screening machine, to cater to the mining and highway construction industries' requirements. Over time, Gilson has expanded its product portfolio and now offers a wide range of equipment, including ovens and furnaces, scales and balances, general laboratory testing equipment, as well as material testing equipment for aggregates, asphalt, concrete, and soils.

Bugger is a distributor of entomological supplies and equipment for insect research founded in 2017 and based in Satakunta, Finland. The company's product offering is segmented into field equipment, preparation equipment, collection supplies, literature, gift items, and conservation products. It sells insect nets, microscopes, insect boxes, books and field guides, and insect-themed accessories. These products, which are sourced from different countries, are designed to meet the needs of a diverse range of customers, from hobbyists to professional entomologists.

■ Characteristics ･ 1103 4 types, 1104 are 2 types ･ The case is an airtight structure that is hard to get dust ･ Compact size ･ It is hard to get ...

Kotech Export is a global manufacturer, supplier, and exporter of scientific instruments and laboratory equipment headquartered in Ambala Cantt, India, and was established in 1998. The company specializes in all types of scientific instruments, educational products, and engineering lab equipment. Its product line consists of microscopes, laboratory glassware and plasticware, surgical disposable products, and educational lab supplies. It also offers engineering electrical and electronic lab trainer kits and various pharmaceutical devices. It is an ISO company with a large scale of lab instruments to serve the needs of educational institutions, research laboratories, and hospitals worldwide.

■ Characteristics ･ Expanding clearly with LED light ･ Enlarged image with less distortion to every corner of the lens ･ 2 lens configuration of as...

Beamdivergencecalculator

■ Characteristics ･ Expanding clearly with LED light -A large lens of 75 × 100 mm expands a wide area at once ･ Under the lens, writing and small d...

Thanks for your kind reply, it is very helpful, and yes I want to focus the beam to the size of the nano-particle with 6 nm radius, but I have 2 questions if you kindly allow:

The Gaussian beam is recognized as one of the most useful light sources. To describe the Gaussian beam, there is a mathematical formula called the paraxial Gaussian beam formula. Today, we’ll learn about this formula, including its limitations, by using the Electromagnetic Waves, Frequency Domain interface in the COMSOL Multiphysics® software. We’ll also provide further detail into a potential cause of error when utilizing this formula. In a later blog post, we’ll provide solutions to the limitations discussed here.

Because the laser beam is an electromagnetic beam, it satisfies the Maxwell equations. The time-harmonic assumption (the wave oscillates at a single frequency in time) changes the Maxwell equations to the frequency domain from the time domain, resulting in the monochromatic (single wavelength) Helmholtz equation. Assuming a certain polarization, it further reduces to a scalar Helmholtz equation, which is written in 2D for the out-of-plane electric field for simplicity:

■ Characteristics ･ Lavision -based eyeglass type loupe by its own circular configuration precision plastic lens ･ Even if the magnification increa...

where w(x), R(x), and \eta(x) are the beam radius as a function of x, the radius of curvature of the wavefront, and the Gouy phase, respectively. The following definitions apply: w(x) = w_0\sqrt{1+\left ( \frac{x}{x_R} \right )^2 }, R(x) = x +\frac{x_R^2}{x}, \eta(x) = \frac 12 {\rm atan} \left ( \frac{x}{x_R} \right ), and x_R = \frac{\pi w_0^2}{\lambda}.

1) I realized that you determine the waist radii depending on the wavelength only, Do you divide it by (pi)?, ignoring the particle radius. The second part of my question is should I depend on one factor only in determining w0 that is wavelength only?

Labcare Scientific, incorporated in 2011 and based in Tamil Nadu, India, is a supplier and exporter of extensive scientific laboratory equipment and instruments. The company primarily supplies industrial measuring instruments, test equipment, entomology lab gear, moisture meters, and laboratory instruments. It also provides nylon filters, LCD digital microscopes, water testing equipment, and weather station equipment. The company adheres to ISO 9001 quality standards, and its products have found application in various sectors, including industrial, entomology, and laboratory sectors.

■ Characteristics ･ Keep a comfortable posture while sitting in the roupe that can be held by hand or viewed ･ For those who are looking for a larg...

･ Portable loupe with high magnification light ･ The case is an airtight structure that is hard to get dust ･ It is hard to get scratched, bright a...

Thanks Yosuke, When I write an expession for x2, as you mentioned above, it shows Syntax error in expression – Expression: x*cos(theta) – y*sin(theta) – Subexpression: – y*sin(the – Position: 14 Error in automatic sequence generation. Is last expression for y2 right, because in both parts there is x? Can I define x and y are equal to 1? Regards Jana

feature ■ New development "Defractive Lens" (multilateral folding structural lens) that suppresses the distortion as much as possible ･ Expanding t...

Dear Yosuke, As you know the gaussian beam source that I asked you about I used it in 3D structure and was represented in my model by analytic functon with the next formula: E(x,y,z)= E0*w0/w(x)*exp(-(y^2+z^2)/w(x)^2)*exp(-i*(k*x-eta(x)+k*(y^2+z^2)/(2*R(x)))) And I wrote the component of electric field in propagation direction as following: (j*d(E(x,y,z),z)/emw.k0) where (z) is the polarization direction and I used it to overcome the paraxial approximation problem if you rememer, but I get this error: { Error in user-defined function. – Function: dE_dE__z__internalArgument Failed to evaluate variable. – Variable: comp1.emw.Ebx – Defined as: exp(i*phase)*(!(comp1.isScalingSystemDomain)*(comp1.es.Ex+((j*d((unit_V_cf*E(x/unit_m_cf,y/unit_m_cf,z/unit_m_cf))/unit_m_cf,z))/comp1.emw.k0))) Failed to evaluate expression. – Expression: comp1.emw.Ebx Failed to evaluate operator. – Operator: mean – Geometry: geom1 } Could you tell me the problem here? Thanks

■ Characteristics ･ Lens angle can be adjusted so that it is easy to look into ･ Large lens stand type loupe ･ The magnification can be changed by ...

Dear Yasmien, Can you please go through our technical support, support@comsol.com? We need to see your model to solve your problem. Thank you. Yosuke

There are additional approaches available for simulating the Gaussian beam in a more rigorous manner, allowing you to push through the limit of the smallest spot size. We will discuss this topic in a future blog post. Stay tuned!

Thank you for this clear and informative demonstration of the paraxial beam functionality in COMSOL! At the moment I am working on in bulk laser material processing of sapphire where I need to define an Gaussian beam entering the material and focusing in the bulk. Since this process is time dependent ( we want to study the behavior ), I am looking for a time dependent description of the Gaussian beam to take into account the varying pulse energy. I noticed that the Gaussian beam is only available in the frequency domain, what do I need to know and model to study this in a time dependent study?