Electric Air Dusters - where to get canned air

 2024-07-19 03:39:14

Microscopes are instruments that are used in science laboratories to visualize very minute objects, such as cells and microorganisms, giving a contrasting image that is magnified.

Thanks much for this. We just did microscopy as a topic and the write-up has really helped me to understand better. Thanks again

Thank you for the support u have done may the Holy Spirit from the Almighty shine upon you to have more knowledge 2 continue making more notes from various topics in microbiology????✍️

A beam of light is passed through the condenser to the specimen. The light transmitted from the specimen enters the objective lens. While passing through the objectives, the transmitted rays are spread so that they appear to come from the bigger objects.

1. Illuminator (Light Source)2. Diaphragm (Iris)3. Condenser4. Condenser Focus Knob5. Rack Stop6. Stage7. Stage Control Knobs8. Nose Piece9. Objective Lens10. Tube (Head)11. Eyepiece (Ocular Lens)12. Diopter Adjustment13. Adjustment Knobs (Fine Adjustment Knob and Coarse Adjustment Knob)14. Arm15. Base16. Light Switch17. Brightness Adjustment

Ans. Condensers are lenses that are used to collect and focus light from the illuminator into the specimen. They are found under the stage next to the diaphragm of the microscope. They play a major role in ensuring clear sharp images are produced with a high magnification of 400X and above. Abbe condenser is a condenser specially designed for high-quality microscopes, which makes the condenser to be movable and allows very high magnification of above 400X. High-quality microscopes normally have a high numerical aperture than objective lenses.

The light is then focused on the eyepiece lens. This lens further magnifies the pre-magnified image coming from the objectives.

The following image was taken by a Konica Minolta A1 with lens set to 200mm (35mm equivalent), and locked in the macro mode. The A1 has a sensor size of 8.8×6.6mm. The image below shows that the vertical direction records about 23mm. Therefore, the magnification is 6.6/23 = 0.29X, or 1:3.8, and Konica Minolta A1's magnification is slightly lower than that of the Coolpix 5700. The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Magnification ofconvexlens

Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Examples Let us use a few examples to illustrate the calculation of magnification of a number of Coolpix cameras. The following image was taken with a Coolpix 4500. Note that the 4500 does not have the highest magnification in the macro mode (i.e., yellow flower icon). Instead, the maximum appears when the lens is zoomed in a little bit passing the "macro zone." The focal length used to take the following image is 19.8mm, which translates to 95.89mm in the 135mm equivalent. This image shows that the vertical direction records about 12.5mm. Since the 4500 has a sensor of type 1/1.8" that has a sensor dimension of 7.176×5.319mm, the magnification is 5.319/12.5 = 0.43X or 1:2.35. This magnification is higher than that of the 5700 (i.e., 0.31X). Therefore, in terms of magnification, the 4500 is better than the 5700 (i.e., 0.43X vs. 0.31X). The following image was taken with a Coolpix 5000 at its nearly maximum magnification. It records 18.5mm along the vertical side. Since the Coolpix 5000 has a sensor size of 8.8×6.6, the magnification is 6.6/18.5 = 0.36X, or 1:2.8. Therefore, in terms of magnification, the 4500 is better than (i.e., 0.43X) the Coolpix 5000 (i.e., 0.36X), which, in turn, is better than the 5700 (i.e., 0.31X). This may explain why people consider the Coolpix 4500 as the king of macro. The following image was taken by a Konica Minolta A1 with lens set to 200mm (35mm equivalent), and locked in the macro mode. The A1 has a sensor size of 8.8×6.6mm. The image below shows that the vertical direction records about 23mm. Therefore, the magnification is 6.6/23 = 0.29X, or 1:3.8, and Konica Minolta A1's magnification is slightly lower than that of the Coolpix 5700. The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

The following image was taken with a Coolpix 5000 at its nearly maximum magnification. It records 18.5mm along the vertical side. Since the Coolpix 5000 has a sensor size of 8.8×6.6, the magnification is 6.6/18.5 = 0.36X, or 1:2.8. Therefore, in terms of magnification, the 4500 is better than (i.e., 0.43X) the Coolpix 5000 (i.e., 0.36X), which, in turn, is better than the 5700 (i.e., 0.31X). This may explain why people consider the Coolpix 4500 as the king of macro. The following image was taken by a Konica Minolta A1 with lens set to 200mm (35mm equivalent), and locked in the macro mode. The A1 has a sensor size of 8.8×6.6mm. The image below shows that the vertical direction records about 23mm. Therefore, the magnification is 6.6/23 = 0.29X, or 1:3.8, and Konica Minolta A1's magnification is slightly lower than that of the Coolpix 5700. The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Having been constructed in the 16th Century, microscopes have revolutionized science with their ability to magnify small objects such as microbial cells, producing images with definitive structures that are identifiable and characterizable.

Ans. The magnification of a lens is defined as the ratio of the height of an image to the height of an object. Microscope magnification measures the total enlargement of the image of an object. Magnification power is the product of eyepiece lens power and objective lens power.

Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Microscopes are generally made up of structural parts for holding and supporting the microscope and its components and the optical parts that are used for magnification and viewing of the specimen images. Modern microscopes have additional electronics and display devices. This description defines the parts of a microscope and the functions they perform to enable the visualization of specimens.

There are different types of microscopes like light microscope, dark-field microscope, phase contrast microscope, electron microscope, fluorescent microscope, etc.

Their ability to function is because they have been constructed with special components that enable them to achieve high magnification levels. They can view very small specimens and distinguish their structural differences, for example, the view of animal and plant cells viewing microscopic bacterial cells.

How to Determine the Maximum Magnification In order to find out the maximum magnification of your camera/lens, the first thing to do is to find out the sensor size. We mentioned earlier that magnification is sensor size independent. But, why is sensor size needed? The answer will be clear very soon. Here is the first step. Open your camera manual and find out what type of sensor your camera has. Your camera manual may simply tell you the sensor is 1/2.7" (e.g., Coolpix SQ and Coolpix 3500), 1/1.8" (e.g., Coolpix 4500), or 2/3" (e.g., Coolpix 5000 and Coolpix 5700). These size values are actually the so-called tube size rather than the actual sensor size. If we use the tube size in our calculation, the error may be around 40% to 50%. Although this error rate may not have a significant impact on actual macro shooting, we would prefer to use the actual sensor size. Any good electronic sensor book will provide you with a table showing the relationship between tube size and the actual sensor size. Here are two handy sites for you to get this information: DP Review and Digital Outback Photo. Here are commonly seen sizes: Tube Size Sensor Size Cameras 1/3.2" 4.536×3.416 Canon A100, A200 1/2.7" 5.27×3.96 Minolta X, Xi; Nikon SQ, 3500 1/2" 6.4×4.8 Nikon 950 1/1.8" 7.176×5.319 Nikon 995, 4500; Olympus C5050 2/3" 8.8×6.6 Sony 717, Minolta 7Hi, A1; Nikon 5000, 5700 APS 23.7×15.6 Nikon D100, D1X The next step is taking a picture with a ruler clearly shown in the horizontal or vertical position. Note that the camera should be in macro mode and should be moved back and forth until the image is the largest. The following image was taken with a 5700 when the magnification is the highest. Then, we count how many millimeters are covered in the image. The image below covers about 21.5mm. This means a subject of length 21.5mm has an image length equal to the vertical dimension of the image sensor. In this case, the vertical dimension of the 5700 sensor is 6.6mm. Therefore, the subject length of 21.5mm has an image length of 6.6mm in the image, and the magnification is 6.6/21.5 = 0.31X, or 1:3.26. In other words, the 5700 has a magnification about 0.31X. The following summarizes what you need to do in order to figure out the magnification your camera has: Find out the sensor dimension of your camera. Place a ruler vertically or horizontally. Then, move your camera back and forth and zoom the lens in and out until the image shown on the LCD is the largest. Take a picture and count the number of millimeter recorded on the image. If the height (resp., width) of the sensor is Y and the recorded height (resp., width) is X, the magnification is X/Y! Examples Let us use a few examples to illustrate the calculation of magnification of a number of Coolpix cameras. The following image was taken with a Coolpix 4500. Note that the 4500 does not have the highest magnification in the macro mode (i.e., yellow flower icon). Instead, the maximum appears when the lens is zoomed in a little bit passing the "macro zone." The focal length used to take the following image is 19.8mm, which translates to 95.89mm in the 135mm equivalent. This image shows that the vertical direction records about 12.5mm. Since the 4500 has a sensor of type 1/1.8" that has a sensor dimension of 7.176×5.319mm, the magnification is 5.319/12.5 = 0.43X or 1:2.35. This magnification is higher than that of the 5700 (i.e., 0.31X). Therefore, in terms of magnification, the 4500 is better than the 5700 (i.e., 0.43X vs. 0.31X). The following image was taken with a Coolpix 5000 at its nearly maximum magnification. It records 18.5mm along the vertical side. Since the Coolpix 5000 has a sensor size of 8.8×6.6, the magnification is 6.6/18.5 = 0.36X, or 1:2.8. Therefore, in terms of magnification, the 4500 is better than (i.e., 0.43X) the Coolpix 5000 (i.e., 0.36X), which, in turn, is better than the 5700 (i.e., 0.31X). This may explain why people consider the Coolpix 4500 as the king of macro. The following image was taken by a Konica Minolta A1 with lens set to 200mm (35mm equivalent), and locked in the macro mode. The A1 has a sensor size of 8.8×6.6mm. The image below shows that the vertical direction records about 23mm. Therefore, the magnification is 6.6/23 = 0.29X, or 1:3.8, and Konica Minolta A1's magnification is slightly lower than that of the Coolpix 5700. The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Thanks for helping me to know the parts and functions of a light microscope. THANKS AGAIN AND I HOPE THAT I WILL DRAW IT IN MY EXAM

Thanks a lot for this wonderful note: It is really helpful, Really appreciate the way all the detail about microscope have been explained

Ans. A microscope is an optical instrument with one or more lens systems that are used to get a clear, magnified image of minute objects or structures that can’t be viewed by the naked eye.

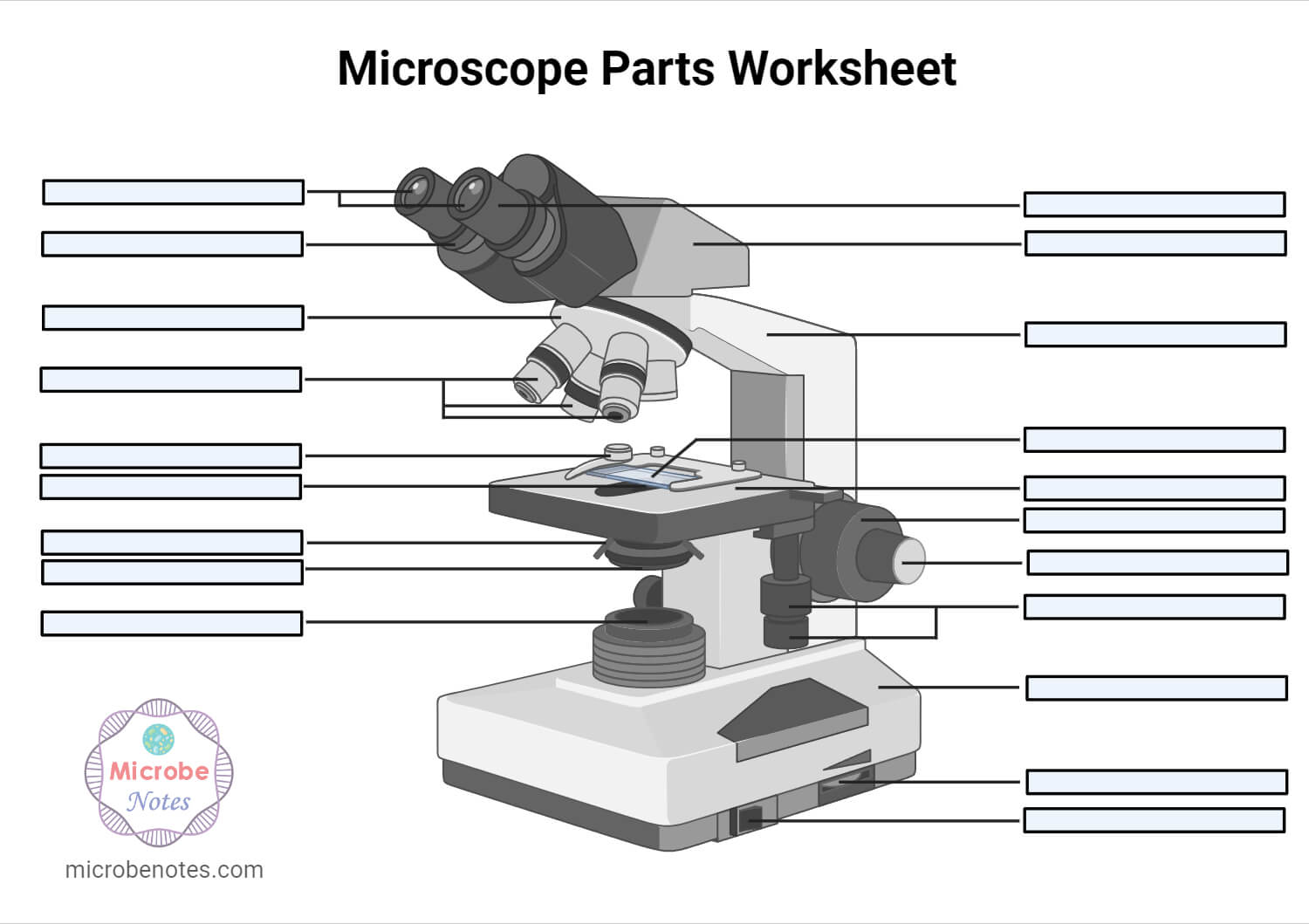
Ans. Rack stop is included in the microscope for preventing the specimen slide from coming too far up and hitting the objective lens.

Magnificationformula for mirror

1. which objective lens focuses closest to object 2. what controls the light entering the binocular lenses 3. how can you enhance the resolving power of a microscope 4. what is useful and false magnification PLEASE CAN YOU HELP ME IN ASWERING THOSE QUESTIONS

I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Therefore, the subject length of 21.5mm has an image length of 6.6mm in the image, and the magnification is 6.6/21.5 = 0.31X, or 1:3.26. In other words, the 5700 has a magnification about 0.31X. The following summarizes what you need to do in order to figure out the magnification your camera has: Find out the sensor dimension of your camera. Place a ruler vertically or horizontally. Then, move your camera back and forth and zoom the lens in and out until the image shown on the LCD is the largest. Take a picture and count the number of millimeter recorded on the image. If the height (resp., width) of the sensor is Y and the recorded height (resp., width) is X, the magnification is X/Y! Examples Let us use a few examples to illustrate the calculation of magnification of a number of Coolpix cameras. The following image was taken with a Coolpix 4500. Note that the 4500 does not have the highest magnification in the macro mode (i.e., yellow flower icon). Instead, the maximum appears when the lens is zoomed in a little bit passing the "macro zone." The focal length used to take the following image is 19.8mm, which translates to 95.89mm in the 135mm equivalent. This image shows that the vertical direction records about 12.5mm. Since the 4500 has a sensor of type 1/1.8" that has a sensor dimension of 7.176×5.319mm, the magnification is 5.319/12.5 = 0.43X or 1:2.35. This magnification is higher than that of the 5700 (i.e., 0.31X). Therefore, in terms of magnification, the 4500 is better than the 5700 (i.e., 0.43X vs. 0.31X). The following image was taken with a Coolpix 5000 at its nearly maximum magnification. It records 18.5mm along the vertical side. Since the Coolpix 5000 has a sensor size of 8.8×6.6, the magnification is 6.6/18.5 = 0.36X, or 1:2.8. Therefore, in terms of magnification, the 4500 is better than (i.e., 0.43X) the Coolpix 5000 (i.e., 0.36X), which, in turn, is better than the 5700 (i.e., 0.31X). This may explain why people consider the Coolpix 4500 as the king of macro. The following image was taken by a Konica Minolta A1 with lens set to 200mm (35mm equivalent), and locked in the macro mode. The A1 has a sensor size of 8.8×6.6mm. The image below shows that the vertical direction records about 23mm. Therefore, the magnification is 6.6/23 = 0.29X, or 1:3.8, and Konica Minolta A1's magnification is slightly lower than that of the Coolpix 5700. The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Ans. The coarse adjustment knob moves the stage up and down to bring the specimen into focus. The fine adjustment knob brings the specimen into sharp focus under low power and is used for all focusing when using high-power lenses.

How to find magnification of a lensusinga

Thank you so much for the note that you have given to me i was so grateful to know that you are so bright people that extend your help to a student

The following summarizes what you need to do in order to figure out the magnification your camera has: Find out the sensor dimension of your camera. Place a ruler vertically or horizontally. Then, move your camera back and forth and zoom the lens in and out until the image shown on the LCD is the largest. Take a picture and count the number of millimeter recorded on the image. If the height (resp., width) of the sensor is Y and the recorded height (resp., width) is X, the magnification is X/Y! Examples Let us use a few examples to illustrate the calculation of magnification of a number of Coolpix cameras. The following image was taken with a Coolpix 4500. Note that the 4500 does not have the highest magnification in the macro mode (i.e., yellow flower icon). Instead, the maximum appears when the lens is zoomed in a little bit passing the "macro zone." The focal length used to take the following image is 19.8mm, which translates to 95.89mm in the 135mm equivalent. This image shows that the vertical direction records about 12.5mm. Since the 4500 has a sensor of type 1/1.8" that has a sensor dimension of 7.176×5.319mm, the magnification is 5.319/12.5 = 0.43X or 1:2.35. This magnification is higher than that of the 5700 (i.e., 0.31X). Therefore, in terms of magnification, the 4500 is better than the 5700 (i.e., 0.43X vs. 0.31X). The following image was taken with a Coolpix 5000 at its nearly maximum magnification. It records 18.5mm along the vertical side. Since the Coolpix 5000 has a sensor size of 8.8×6.6, the magnification is 6.6/18.5 = 0.36X, or 1:2.8. Therefore, in terms of magnification, the 4500 is better than (i.e., 0.43X) the Coolpix 5000 (i.e., 0.36X), which, in turn, is better than the 5700 (i.e., 0.31X). This may explain why people consider the Coolpix 4500 as the king of macro. The following image was taken by a Konica Minolta A1 with lens set to 200mm (35mm equivalent), and locked in the macro mode. The A1 has a sensor size of 8.8×6.6mm. The image below shows that the vertical direction records about 23mm. Therefore, the magnification is 6.6/23 = 0.29X, or 1:3.8, and Konica Minolta A1's magnification is slightly lower than that of the Coolpix 5700. The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Magnification of lens

Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Thank you very much it really helped me with my science home work since i in 8th grade and this my home work to draw a microscope label all the parts and the function thank may the holy father of holy spirits bless you and give more wisdom thanks love you all keep up the good work and thank you again bye.

Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

How tocalculatemagnificationmicroscope

Thanks very much dear and please continue doing so, am Gerald M from Uganda East Africa doing diploma in nursing at Mulago school of nursing and midwifery

The next step is taking a picture with a ruler clearly shown in the horizontal or vertical position. Note that the camera should be in macro mode and should be moved back and forth until the image is the largest. The following image was taken with a 5700 when the magnification is the highest. Then, we count how many millimeters are covered in the image. The image below covers about 21.5mm. This means a subject of length 21.5mm has an image length equal to the vertical dimension of the image sensor. In this case, the vertical dimension of the 5700 sensor is 6.6mm. Therefore, the subject length of 21.5mm has an image length of 6.6mm in the image, and the magnification is 6.6/21.5 = 0.31X, or 1:3.26. In other words, the 5700 has a magnification about 0.31X. The following summarizes what you need to do in order to figure out the magnification your camera has: Find out the sensor dimension of your camera. Place a ruler vertically or horizontally. Then, move your camera back and forth and zoom the lens in and out until the image shown on the LCD is the largest. Take a picture and count the number of millimeter recorded on the image. If the height (resp., width) of the sensor is Y and the recorded height (resp., width) is X, the magnification is X/Y! Examples Let us use a few examples to illustrate the calculation of magnification of a number of Coolpix cameras. The following image was taken with a Coolpix 4500. Note that the 4500 does not have the highest magnification in the macro mode (i.e., yellow flower icon). Instead, the maximum appears when the lens is zoomed in a little bit passing the "macro zone." The focal length used to take the following image is 19.8mm, which translates to 95.89mm in the 135mm equivalent. This image shows that the vertical direction records about 12.5mm. Since the 4500 has a sensor of type 1/1.8" that has a sensor dimension of 7.176×5.319mm, the magnification is 5.319/12.5 = 0.43X or 1:2.35. This magnification is higher than that of the 5700 (i.e., 0.31X). Therefore, in terms of magnification, the 4500 is better than the 5700 (i.e., 0.43X vs. 0.31X). The following image was taken with a Coolpix 5000 at its nearly maximum magnification. It records 18.5mm along the vertical side. Since the Coolpix 5000 has a sensor size of 8.8×6.6, the magnification is 6.6/18.5 = 0.36X, or 1:2.8. Therefore, in terms of magnification, the 4500 is better than (i.e., 0.43X) the Coolpix 5000 (i.e., 0.36X), which, in turn, is better than the 5700 (i.e., 0.31X). This may explain why people consider the Coolpix 4500 as the king of macro. The following image was taken by a Konica Minolta A1 with lens set to 200mm (35mm equivalent), and locked in the macro mode. The A1 has a sensor size of 8.8×6.6mm. The image below shows that the vertical direction records about 23mm. Therefore, the magnification is 6.6/23 = 0.29X, or 1:3.8, and Konica Minolta A1's magnification is slightly lower than that of the Coolpix 5700. The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Seriously, if i am not grateful, i am lying. This note is really helpeful to me to differet ways to different methology.

Ans. The eyepiece, also known as the ocular is the part used to look through the microscope. Its found at the top of the microscope. Its standard magnification is 10x with an optional eyepiece having magnifications from 5X – 30X. Objective Lens are the major lenses used for specimen visualization. They have a magnification power of 40x-100x. There are about 1- 4 objective lenses placed on one microscope, in that some are rare facing and others face forward.

Magnificationformula Biology

Let us use a few examples to illustrate the calculation of magnification of a number of Coolpix cameras. The following image was taken with a Coolpix 4500. Note that the 4500 does not have the highest magnification in the macro mode (i.e., yellow flower icon). Instead, the maximum appears when the lens is zoomed in a little bit passing the "macro zone." The focal length used to take the following image is 19.8mm, which translates to 95.89mm in the 135mm equivalent. This image shows that the vertical direction records about 12.5mm. Since the 4500 has a sensor of type 1/1.8" that has a sensor dimension of 7.176×5.319mm, the magnification is 5.319/12.5 = 0.43X or 1:2.35. This magnification is higher than that of the 5700 (i.e., 0.31X). Therefore, in terms of magnification, the 4500 is better than the 5700 (i.e., 0.43X vs. 0.31X). The following image was taken with a Coolpix 5000 at its nearly maximum magnification. It records 18.5mm along the vertical side. Since the Coolpix 5000 has a sensor size of 8.8×6.6, the magnification is 6.6/18.5 = 0.36X, or 1:2.8. Therefore, in terms of magnification, the 4500 is better than (i.e., 0.43X) the Coolpix 5000 (i.e., 0.36X), which, in turn, is better than the 5700 (i.e., 0.31X). This may explain why people consider the Coolpix 4500 as the king of macro. The following image was taken by a Konica Minolta A1 with lens set to 200mm (35mm equivalent), and locked in the macro mode. The A1 has a sensor size of 8.8×6.6mm. The image below shows that the vertical direction records about 23mm. Therefore, the magnification is 6.6/23 = 0.29X, or 1:3.8, and Konica Minolta A1's magnification is slightly lower than that of the Coolpix 5700. The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Magnificationformula forlensin termsoffocal length

There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

it very good website i use in 4 grade right after i plai amog us and they vote me out using orang strat witch mad me sad 🙁

Thanks alot of your help and knowI can draw it well in my exams and write the functions.Thankyou very much for your help

1. Ocular Lens (Eye Piece)2. Diopter Adjustment3. Head4. Nose Piece5. Objective Lens6. Arm (Carrying Handle)7. Mechanical Stage8. Stage Clip9. Aperture10. Diaphragm11. Condenser12. Coarse Adjustment13. Fine Adjustment14. Illuminator (Light Source)15. Stage Controls16. Base17. Brightness Adjustment18. Light Switch

Normally, the magnification of a lens is written in a slightly different form rather than as a single number. If the magnification is Y/X, where Y and X are image length and subject length, respectively, the commonly used form is first written as Y:X. Thus, the example discussed in the previous paragraph has a magnification of 2:10. Sometimes, we also divide both X and Y by either X or Y to obtain a form like 1:Y/X or a form like X/Y:1. Thus, 2:10 may also be rewritten as 1:5 or 0.2:1. The life-size magnification is rewritten as 1:1, and 2:1 and 1:2 are larger than and smaller than life-size, respectively. Conversely, when we see a magnification value like 3:4, we know that it is equal to 3/4=0.75X, which is smaller than life-size. Similarly, a magnification of 5:2 is equal to 5/2=2.5X, which is larger than life-size. How to Determine the Maximum Magnification In order to find out the maximum magnification of your camera/lens, the first thing to do is to find out the sensor size. We mentioned earlier that magnification is sensor size independent. But, why is sensor size needed? The answer will be clear very soon. Here is the first step. Open your camera manual and find out what type of sensor your camera has. Your camera manual may simply tell you the sensor is 1/2.7" (e.g., Coolpix SQ and Coolpix 3500), 1/1.8" (e.g., Coolpix 4500), or 2/3" (e.g., Coolpix 5000 and Coolpix 5700). These size values are actually the so-called tube size rather than the actual sensor size. If we use the tube size in our calculation, the error may be around 40% to 50%. Although this error rate may not have a significant impact on actual macro shooting, we would prefer to use the actual sensor size. Any good electronic sensor book will provide you with a table showing the relationship between tube size and the actual sensor size. Here are two handy sites for you to get this information: DP Review and Digital Outback Photo. Here are commonly seen sizes: Tube Size Sensor Size Cameras 1/3.2" 4.536×3.416 Canon A100, A200 1/2.7" 5.27×3.96 Minolta X, Xi; Nikon SQ, 3500 1/2" 6.4×4.8 Nikon 950 1/1.8" 7.176×5.319 Nikon 995, 4500; Olympus C5050 2/3" 8.8×6.6 Sony 717, Minolta 7Hi, A1; Nikon 5000, 5700 APS 23.7×15.6 Nikon D100, D1X The next step is taking a picture with a ruler clearly shown in the horizontal or vertical position. Note that the camera should be in macro mode and should be moved back and forth until the image is the largest. The following image was taken with a 5700 when the magnification is the highest. Then, we count how many millimeters are covered in the image. The image below covers about 21.5mm. This means a subject of length 21.5mm has an image length equal to the vertical dimension of the image sensor. In this case, the vertical dimension of the 5700 sensor is 6.6mm. Therefore, the subject length of 21.5mm has an image length of 6.6mm in the image, and the magnification is 6.6/21.5 = 0.31X, or 1:3.26. In other words, the 5700 has a magnification about 0.31X. The following summarizes what you need to do in order to figure out the magnification your camera has: Find out the sensor dimension of your camera. Place a ruler vertically or horizontally. Then, move your camera back and forth and zoom the lens in and out until the image shown on the LCD is the largest. Take a picture and count the number of millimeter recorded on the image. If the height (resp., width) of the sensor is Y and the recorded height (resp., width) is X, the magnification is X/Y! Examples Let us use a few examples to illustrate the calculation of magnification of a number of Coolpix cameras. The following image was taken with a Coolpix 4500. Note that the 4500 does not have the highest magnification in the macro mode (i.e., yellow flower icon). Instead, the maximum appears when the lens is zoomed in a little bit passing the "macro zone." The focal length used to take the following image is 19.8mm, which translates to 95.89mm in the 135mm equivalent. This image shows that the vertical direction records about 12.5mm. Since the 4500 has a sensor of type 1/1.8" that has a sensor dimension of 7.176×5.319mm, the magnification is 5.319/12.5 = 0.43X or 1:2.35. This magnification is higher than that of the 5700 (i.e., 0.31X). Therefore, in terms of magnification, the 4500 is better than the 5700 (i.e., 0.43X vs. 0.31X). The following image was taken with a Coolpix 5000 at its nearly maximum magnification. It records 18.5mm along the vertical side. Since the Coolpix 5000 has a sensor size of 8.8×6.6, the magnification is 6.6/18.5 = 0.36X, or 1:2.8. Therefore, in terms of magnification, the 4500 is better than (i.e., 0.43X) the Coolpix 5000 (i.e., 0.36X), which, in turn, is better than the 5700 (i.e., 0.31X). This may explain why people consider the Coolpix 4500 as the king of macro. The following image was taken by a Konica Minolta A1 with lens set to 200mm (35mm equivalent), and locked in the macro mode. The A1 has a sensor size of 8.8×6.6mm. The image below shows that the vertical direction records about 23mm. Therefore, the magnification is 6.6/23 = 0.29X, or 1:3.8, and Konica Minolta A1's magnification is slightly lower than that of the Coolpix 5700. The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

In order to find out the maximum magnification of your camera/lens, the first thing to do is to find out the sensor size. We mentioned earlier that magnification is sensor size independent. But, why is sensor size needed? The answer will be clear very soon. Here is the first step. Open your camera manual and find out what type of sensor your camera has. Your camera manual may simply tell you the sensor is 1/2.7" (e.g., Coolpix SQ and Coolpix 3500), 1/1.8" (e.g., Coolpix 4500), or 2/3" (e.g., Coolpix 5000 and Coolpix 5700). These size values are actually the so-called tube size rather than the actual sensor size. If we use the tube size in our calculation, the error may be around 40% to 50%. Although this error rate may not have a significant impact on actual macro shooting, we would prefer to use the actual sensor size. Any good electronic sensor book will provide you with a table showing the relationship between tube size and the actual sensor size. Here are two handy sites for you to get this information: DP Review and Digital Outback Photo. Here are commonly seen sizes: Tube Size Sensor Size Cameras 1/3.2" 4.536×3.416 Canon A100, A200 1/2.7" 5.27×3.96 Minolta X, Xi; Nikon SQ, 3500 1/2" 6.4×4.8 Nikon 950 1/1.8" 7.176×5.319 Nikon 995, 4500; Olympus C5050 2/3" 8.8×6.6 Sony 717, Minolta 7Hi, A1; Nikon 5000, 5700 APS 23.7×15.6 Nikon D100, D1X The next step is taking a picture with a ruler clearly shown in the horizontal or vertical position. Note that the camera should be in macro mode and should be moved back and forth until the image is the largest. The following image was taken with a 5700 when the magnification is the highest. Then, we count how many millimeters are covered in the image. The image below covers about 21.5mm. This means a subject of length 21.5mm has an image length equal to the vertical dimension of the image sensor. In this case, the vertical dimension of the 5700 sensor is 6.6mm. Therefore, the subject length of 21.5mm has an image length of 6.6mm in the image, and the magnification is 6.6/21.5 = 0.31X, or 1:3.26. In other words, the 5700 has a magnification about 0.31X. The following summarizes what you need to do in order to figure out the magnification your camera has: Find out the sensor dimension of your camera. Place a ruler vertically or horizontally. Then, move your camera back and forth and zoom the lens in and out until the image shown on the LCD is the largest. Take a picture and count the number of millimeter recorded on the image. If the height (resp., width) of the sensor is Y and the recorded height (resp., width) is X, the magnification is X/Y! Examples Let us use a few examples to illustrate the calculation of magnification of a number of Coolpix cameras. The following image was taken with a Coolpix 4500. Note that the 4500 does not have the highest magnification in the macro mode (i.e., yellow flower icon). Instead, the maximum appears when the lens is zoomed in a little bit passing the "macro zone." The focal length used to take the following image is 19.8mm, which translates to 95.89mm in the 135mm equivalent. This image shows that the vertical direction records about 12.5mm. Since the 4500 has a sensor of type 1/1.8" that has a sensor dimension of 7.176×5.319mm, the magnification is 5.319/12.5 = 0.43X or 1:2.35. This magnification is higher than that of the 5700 (i.e., 0.31X). Therefore, in terms of magnification, the 4500 is better than the 5700 (i.e., 0.43X vs. 0.31X). The following image was taken with a Coolpix 5000 at its nearly maximum magnification. It records 18.5mm along the vertical side. Since the Coolpix 5000 has a sensor size of 8.8×6.6, the magnification is 6.6/18.5 = 0.36X, or 1:2.8. Therefore, in terms of magnification, the 4500 is better than (i.e., 0.43X) the Coolpix 5000 (i.e., 0.36X), which, in turn, is better than the 5700 (i.e., 0.31X). This may explain why people consider the Coolpix 4500 as the king of macro. The following image was taken by a Konica Minolta A1 with lens set to 200mm (35mm equivalent), and locked in the macro mode. The A1 has a sensor size of 8.8×6.6mm. The image below shows that the vertical direction records about 23mm. Therefore, the magnification is 6.6/23 = 0.29X, or 1:3.8, and Konica Minolta A1's magnification is slightly lower than that of the Coolpix 5700. The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Microscopes are made up of lenses for magnification, each with its own magnification powers. Depending on the type of lens, it will magnify the specimen according to its focal strength.

I did NOT like this website sourse. Wanna know why I didn’t like it??? I don’t like it BECAUSE my school wants me to use this website sourse. My new science teacher wants us to answer those 10 questions. I think its pretty dumb. No Offensen to anyne out there, because I am a nice person not a mean one.

4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

The magnification of a lens means how large (or small) a subject can be reproduced on the image plane (e.g., film and image sensor). The definition of magnification is very simple. If a subject of length X forms an image of length Y in the image, the magnification of the lens is defined to be Y/X. This is the lateral magnification of a lens, which is commonly used for close-up and macro photography, because it only measures in one dimension. For example, if a subject of length 10mm has a length of 2mm on the image, the magnification of the lens is 2/10=0.2. If a lens can produce a magnification equal to 1, we will say it can deliver a life-size image; and if the magnification is larger (resp., smaller) than 1, we will say it delivers a larger (resp., smaller) than life-size image. Note that magnification does not depend on the film frame size and sensor size since it is a lens characteristic. For example, the Nikon AF 60mm F2.8D Micro is capable of life-size magnification on a Nikon film camera. If this lens is used with an APS size Nikon DSLR body such as D2H, D100 and D70, it still delivers a life-size magnification. Normally, the magnification of a lens is written in a slightly different form rather than as a single number. If the magnification is Y/X, where Y and X are image length and subject length, respectively, the commonly used form is first written as Y:X. Thus, the example discussed in the previous paragraph has a magnification of 2:10. Sometimes, we also divide both X and Y by either X or Y to obtain a form like 1:Y/X or a form like X/Y:1. Thus, 2:10 may also be rewritten as 1:5 or 0.2:1. The life-size magnification is rewritten as 1:1, and 2:1 and 1:2 are larger than and smaller than life-size, respectively. Conversely, when we see a magnification value like 3:4, we know that it is equal to 3/4=0.75X, which is smaller than life-size. Similarly, a magnification of 5:2 is equal to 5/2=2.5X, which is larger than life-size. How to Determine the Maximum Magnification In order to find out the maximum magnification of your camera/lens, the first thing to do is to find out the sensor size. We mentioned earlier that magnification is sensor size independent. But, why is sensor size needed? The answer will be clear very soon. Here is the first step. Open your camera manual and find out what type of sensor your camera has. Your camera manual may simply tell you the sensor is 1/2.7" (e.g., Coolpix SQ and Coolpix 3500), 1/1.8" (e.g., Coolpix 4500), or 2/3" (e.g., Coolpix 5000 and Coolpix 5700). These size values are actually the so-called tube size rather than the actual sensor size. If we use the tube size in our calculation, the error may be around 40% to 50%. Although this error rate may not have a significant impact on actual macro shooting, we would prefer to use the actual sensor size. Any good electronic sensor book will provide you with a table showing the relationship between tube size and the actual sensor size. Here are two handy sites for you to get this information: DP Review and Digital Outback Photo. Here are commonly seen sizes: Tube Size Sensor Size Cameras 1/3.2" 4.536×3.416 Canon A100, A200 1/2.7" 5.27×3.96 Minolta X, Xi; Nikon SQ, 3500 1/2" 6.4×4.8 Nikon 950 1/1.8" 7.176×5.319 Nikon 995, 4500; Olympus C5050 2/3" 8.8×6.6 Sony 717, Minolta 7Hi, A1; Nikon 5000, 5700 APS 23.7×15.6 Nikon D100, D1X The next step is taking a picture with a ruler clearly shown in the horizontal or vertical position. Note that the camera should be in macro mode and should be moved back and forth until the image is the largest. The following image was taken with a 5700 when the magnification is the highest. Then, we count how many millimeters are covered in the image. The image below covers about 21.5mm. This means a subject of length 21.5mm has an image length equal to the vertical dimension of the image sensor. In this case, the vertical dimension of the 5700 sensor is 6.6mm. Therefore, the subject length of 21.5mm has an image length of 6.6mm in the image, and the magnification is 6.6/21.5 = 0.31X, or 1:3.26. In other words, the 5700 has a magnification about 0.31X. The following summarizes what you need to do in order to figure out the magnification your camera has: Find out the sensor dimension of your camera. Place a ruler vertically or horizontally. Then, move your camera back and forth and zoom the lens in and out until the image shown on the LCD is the largest. Take a picture and count the number of millimeter recorded on the image. If the height (resp., width) of the sensor is Y and the recorded height (resp., width) is X, the magnification is X/Y! Examples Let us use a few examples to illustrate the calculation of magnification of a number of Coolpix cameras. The following image was taken with a Coolpix 4500. Note that the 4500 does not have the highest magnification in the macro mode (i.e., yellow flower icon). Instead, the maximum appears when the lens is zoomed in a little bit passing the "macro zone." The focal length used to take the following image is 19.8mm, which translates to 95.89mm in the 135mm equivalent. This image shows that the vertical direction records about 12.5mm. Since the 4500 has a sensor of type 1/1.8" that has a sensor dimension of 7.176×5.319mm, the magnification is 5.319/12.5 = 0.43X or 1:2.35. This magnification is higher than that of the 5700 (i.e., 0.31X). Therefore, in terms of magnification, the 4500 is better than the 5700 (i.e., 0.43X vs. 0.31X). The following image was taken with a Coolpix 5000 at its nearly maximum magnification. It records 18.5mm along the vertical side. Since the Coolpix 5000 has a sensor size of 8.8×6.6, the magnification is 6.6/18.5 = 0.36X, or 1:2.8. Therefore, in terms of magnification, the 4500 is better than (i.e., 0.43X) the Coolpix 5000 (i.e., 0.36X), which, in turn, is better than the 5700 (i.e., 0.31X). This may explain why people consider the Coolpix 4500 as the king of macro. The following image was taken by a Konica Minolta A1 with lens set to 200mm (35mm equivalent), and locked in the macro mode. The A1 has a sensor size of 8.8×6.6mm. The image below shows that the vertical direction records about 23mm. Therefore, the magnification is 6.6/23 = 0.29X, or 1:3.8, and Konica Minolta A1's magnification is slightly lower than that of the Coolpix 5700. The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Lensformula

Tube Size Sensor Size Cameras 1/3.2" 4.536×3.416 Canon A100, A200 1/2.7" 5.27×3.96 Minolta X, Xi; Nikon SQ, 3500 1/2" 6.4×4.8 Nikon 950 1/1.8" 7.176×5.319 Nikon 995, 4500; Olympus C5050 2/3" 8.8×6.6 Sony 717, Minolta 7Hi, A1; Nikon 5000, 5700 APS 23.7×15.6 Nikon D100, D1X The next step is taking a picture with a ruler clearly shown in the horizontal or vertical position. Note that the camera should be in macro mode and should be moved back and forth until the image is the largest. The following image was taken with a 5700 when the magnification is the highest. Then, we count how many millimeters are covered in the image. The image below covers about 21.5mm. This means a subject of length 21.5mm has an image length equal to the vertical dimension of the image sensor. In this case, the vertical dimension of the 5700 sensor is 6.6mm. Therefore, the subject length of 21.5mm has an image length of 6.6mm in the image, and the magnification is 6.6/21.5 = 0.31X, or 1:3.26. In other words, the 5700 has a magnification about 0.31X. The following summarizes what you need to do in order to figure out the magnification your camera has: Find out the sensor dimension of your camera. Place a ruler vertically or horizontally. Then, move your camera back and forth and zoom the lens in and out until the image shown on the LCD is the largest. Take a picture and count the number of millimeter recorded on the image. If the height (resp., width) of the sensor is Y and the recorded height (resp., width) is X, the magnification is X/Y! Examples Let us use a few examples to illustrate the calculation of magnification of a number of Coolpix cameras. The following image was taken with a Coolpix 4500. Note that the 4500 does not have the highest magnification in the macro mode (i.e., yellow flower icon). Instead, the maximum appears when the lens is zoomed in a little bit passing the "macro zone." The focal length used to take the following image is 19.8mm, which translates to 95.89mm in the 135mm equivalent. This image shows that the vertical direction records about 12.5mm. Since the 4500 has a sensor of type 1/1.8" that has a sensor dimension of 7.176×5.319mm, the magnification is 5.319/12.5 = 0.43X or 1:2.35. This magnification is higher than that of the 5700 (i.e., 0.31X). Therefore, in terms of magnification, the 4500 is better than the 5700 (i.e., 0.43X vs. 0.31X). The following image was taken with a Coolpix 5000 at its nearly maximum magnification. It records 18.5mm along the vertical side. Since the Coolpix 5000 has a sensor size of 8.8×6.6, the magnification is 6.6/18.5 = 0.36X, or 1:2.8. Therefore, in terms of magnification, the 4500 is better than (i.e., 0.43X) the Coolpix 5000 (i.e., 0.36X), which, in turn, is better than the 5700 (i.e., 0.31X). This may explain why people consider the Coolpix 4500 as the king of macro. The following image was taken by a Konica Minolta A1 with lens set to 200mm (35mm equivalent), and locked in the macro mode. The A1 has a sensor size of 8.8×6.6mm. The image below shows that the vertical direction records about 23mm. Therefore, the magnification is 6.6/23 = 0.29X, or 1:3.8, and Konica Minolta A1's magnification is slightly lower than that of the Coolpix 5700. The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Here is the first step. Open your camera manual and find out what type of sensor your camera has. Your camera manual may simply tell you the sensor is 1/2.7" (e.g., Coolpix SQ and Coolpix 3500), 1/1.8" (e.g., Coolpix 4500), or 2/3" (e.g., Coolpix 5000 and Coolpix 5700). These size values are actually the so-called tube size rather than the actual sensor size. If we use the tube size in our calculation, the error may be around 40% to 50%. Although this error rate may not have a significant impact on actual macro shooting, we would prefer to use the actual sensor size. Any good electronic sensor book will provide you with a table showing the relationship between tube size and the actual sensor size. Here are two handy sites for you to get this information: DP Review and Digital Outback Photo. Here are commonly seen sizes: Tube Size Sensor Size Cameras 1/3.2" 4.536×3.416 Canon A100, A200 1/2.7" 5.27×3.96 Minolta X, Xi; Nikon SQ, 3500 1/2" 6.4×4.8 Nikon 950 1/1.8" 7.176×5.319 Nikon 995, 4500; Olympus C5050 2/3" 8.8×6.6 Sony 717, Minolta 7Hi, A1; Nikon 5000, 5700 APS 23.7×15.6 Nikon D100, D1X The next step is taking a picture with a ruler clearly shown in the horizontal or vertical position. Note that the camera should be in macro mode and should be moved back and forth until the image is the largest. The following image was taken with a 5700 when the magnification is the highest. Then, we count how many millimeters are covered in the image. The image below covers about 21.5mm. This means a subject of length 21.5mm has an image length equal to the vertical dimension of the image sensor. In this case, the vertical dimension of the 5700 sensor is 6.6mm. Therefore, the subject length of 21.5mm has an image length of 6.6mm in the image, and the magnification is 6.6/21.5 = 0.31X, or 1:3.26. In other words, the 5700 has a magnification about 0.31X. The following summarizes what you need to do in order to figure out the magnification your camera has: Find out the sensor dimension of your camera. Place a ruler vertically or horizontally. Then, move your camera back and forth and zoom the lens in and out until the image shown on the LCD is the largest. Take a picture and count the number of millimeter recorded on the image. If the height (resp., width) of the sensor is Y and the recorded height (resp., width) is X, the magnification is X/Y! Examples Let us use a few examples to illustrate the calculation of magnification of a number of Coolpix cameras. The following image was taken with a Coolpix 4500. Note that the 4500 does not have the highest magnification in the macro mode (i.e., yellow flower icon). Instead, the maximum appears when the lens is zoomed in a little bit passing the "macro zone." The focal length used to take the following image is 19.8mm, which translates to 95.89mm in the 135mm equivalent. This image shows that the vertical direction records about 12.5mm. Since the 4500 has a sensor of type 1/1.8" that has a sensor dimension of 7.176×5.319mm, the magnification is 5.319/12.5 = 0.43X or 1:2.35. This magnification is higher than that of the 5700 (i.e., 0.31X). Therefore, in terms of magnification, the 4500 is better than the 5700 (i.e., 0.43X vs. 0.31X). The following image was taken with a Coolpix 5000 at its nearly maximum magnification. It records 18.5mm along the vertical side. Since the Coolpix 5000 has a sensor size of 8.8×6.6, the magnification is 6.6/18.5 = 0.36X, or 1:2.8. Therefore, in terms of magnification, the 4500 is better than (i.e., 0.43X) the Coolpix 5000 (i.e., 0.36X), which, in turn, is better than the 5700 (i.e., 0.31X). This may explain why people consider the Coolpix 4500 as the king of macro. The following image was taken by a Konica Minolta A1 with lens set to 200mm (35mm equivalent), and locked in the macro mode. The A1 has a sensor size of 8.8×6.6mm. The image below shows that the vertical direction records about 23mm. Therefore, the magnification is 6.6/23 = 0.29X, or 1:3.8, and Konica Minolta A1's magnification is slightly lower than that of the Coolpix 5700. The following image was taken by a Nikon D100 with a Nikon AF 60mm F2.8D Micro lens that is capable of 1:1 life-size. The recorded "height" is about 15.5mm on the image. Since the "height" of the D100 sensor is 15.6mm, we see that the magnification is 15.6/15.5 = 1X, or 1:1. This illustrates an important fact that magnification is a lens characteristic and independent of the image size. The following table summarizes the magnification results. Camera+Lens Recorded Length Magnification Coolpix 4500 12.5mm 0.43X or 1:2.35 Coolpix 5000 18.5mm 0.36X or 1:2.8 Coolpix 5700 21.5mm 0.31X or 1:3.26 Minolta A1 23mm 0.29X or 1:3.8 D100 + 60mm Micro 15.5mm 1X or 1:1 Any Inaccuracy? Yes, of course, there are some inaccuracies. Here are the major ones. Even though we know the sensor size, since the area used for recording an image is usually slightly smaller than the size of the sensor, the "height" value would be slightly smaller, which, in turn, makes the calculated magnification slightly lower. Moreover, the image taking task for determining the maximum magnification is basically a trial-and-error process, discrepancies may be introduced from time to time. The recorded "height" may not always be the same value, and the calculated magnification will also be affected. Fortunately, the impact of these two factors on the calculated magnification is not very significant (i.e., 0.29X and 0.31X do not have much difference in reality). If you wish to carry out the magnification calculation discussed here, you may want to take several images and choose the best one. Don't You Feel a Little Odd? I am not sure if you see something odd in the above five images used for magnification calculation. The follow shows their smaller size images. Do you see anything unusual? If you examine the images below, you will see that the magnifications of 4500, 5000, 5700 and A1 are 0.43X, 0.36X, 0.31X and 0.29X. This is obvious because the images justify this fact (i.e., the image taken by the 4500 covers a smaller area than that of the 5000, etc). But, the image taken by the D100 plus a 1:1 capable 60mm Micro lens covers a larger area than that of the 4500. Is there something wrong? The answer is nothing wrong here. But, why the 4500 with a magnification 0.43X can "magnify" higher than a 1:1 life-size image taken by the D100 plus 60mm Micro lens? The answer is: the sensor size of the D100 is larger than the sensor of the 4500. 4500 (0.43X) 5000 (0.36X) 5700 (0.31X) Minolta A1 (0.29X) D100 + 60mm Micro (1X) Suppose a lens projects a given subject 1:1 life-size on an image sensor of dimension a×b. Suppose further the same subject is projected on another image sensor by a lens capable of 1:r. If the second sensor records the same coverage as the first one, the second sensor must have a dimension of (a/r)×(b/r). For example, suppose a subject projects 1:1 on an image sensor A of 3×4, and the same subject projects by a lens capable of 1:4 on another image sensor B. Then, sensor B must have a dimension of at least (3/4)×(4/4) = 0.75×1 in order to record a complete image of the given subject. Therefore, a lens of 1:r and a sensor of dimension (a/r)×(b/r) would yield the same result that a 1:1 lens and a a×b sensor can obtain. This result shows the advantage of smaller size sensors because they can achieve the same result that a 1:1 lens can get with a lower magnification. Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

Some authors prefer to use "coverage" as a measure of the macro capability of a camera. In the above examples, since the 4500, 5000, 5700 and Minolta A1 use a 4×3 format and the D100 uses a 3×2 format, we can easily calculate the coverage of each camera. Basically, if the image shows p mm as the "height", then the width is p×4/3. As for the DSLR case, it is p×3/2. The following table summarizes the coverage area of 4500, 5000, 5700, Minolta A1 and D100 with AF 60mm F2.8D. From this table, we learn that the D100 with a 1:1 life-size capable lens has a coverage larger than that of the 4500. This, of course, does not reflect the actual capability of the lens being used. Note that magnification can be calculated from the coverage data and sensor size. For example, since the coverage of the 5000 is 24.67×18.5 and the sensor size is 8.8×6.6, the magnification of the 5000 is 6.6/18.5 = 0.36X. Camera Magnification Recorded Height Aspect Ratio Coverage Coolpix 4500 0.43X 12.5mm 4:3 16.67×12.5mm Coolpix 5000 0.36X 18.5mm 4:3 24.67×18.5mm Coolpix 5700 0.31X 21.5mm 4:3 28.67×21.5mm Minolta A1 0.29X 23mm 4:3 30.67×23mm Nikon D100 + 60mm Micro 1X 15.5mm 3:2 23.25×15.5mm Some suggested to factor in the resolution of the sensor. Suppose the coverage and resolution of the sensor are a×b and m×n, respectively. Some suggest the use of m/a = n/b as a measure of the macro capability of a lens+sensor system and claim that higher value implies better macro. Let us examine this approach closely. The following table shows the calculated results of the five cameras mentioned above. The results look fine so far, except for the D100 case, again. Consider the Coolpix 8700. Since this camera has the same lens and sensor size (i.e., 2/3") as that of the 5700, we can assume that the coverage would be same as that of the 5700. However, since the 8700 has a resolution of 3264×2448, the pixel/mm count jumps to 2448/21.5 = 113.86. What if we use a 12mp 2/3" sensor with a resolution of 4000×3000 as a replacement of the 5700/8700 sensor? The pixel/mm count would be 3000/21.5 = 139.53, which is even higher than that of the 4500! Is there something unusual here? Yes, if we continue to pack more pixels to a 2/3" sensor, the pixel/mm count increases, and, as a result, the "macro" capability in this sense increases even though the lens magnification and image coverage do not change. Therefore, this is a problematic definition because macro capability does not come from pixel count. Those who promote this pixel/mm count as a measurement of macro capability usually have an argument like this: one can crop part of the image, because the increase of pixel count cropping would increase the magnification. Unfortunately, cropping is not part of the equation of magnification. Otherwise, one does not need any macro lens. A very high density and small sensor would do all the magic of an excellent macro lens. Camera Magnification Coverage Resolution Pixels/mm Coolpix 4500 0.43X 16.67×12.5 2272×1704 136.32 Coolpix 5000 0.36X 24.67×18.5 2560×1920 103.78 Coolpix 5700 0.31X 28.67×21.5 2560×1960 89.30 Minolta A1 0.29X 30.67×23 2560×1960 83.48 Nikon D100 + 60mm Micro 1X 23.25×15.5 3008×2000 129.03 There are other problems with the "pixel/mm count" approach. Both take the image device into consideration, while the traditional magnification approach is image device independent. Recall that a lens of 1:r magnification needs a sensor of size (a/r)×(b/r) to produce an image of a subject of size a×b, while a 1:1 life-size lens can produce the same subject on a sensor of dimension a×b. Therefore, if the resolution of both sensors of dimension a×b and (a/r)×(b/r) are the same, the pixel size of the latter would be 1:r of the former measured in diameter. This means the lens designed for the (a/r)×(b/r) sensor must resolve r times higher than the lens designed for the a×b sensor to achieve the same sharpness. This extra resolving power is not represented in the "pixel/mm" approaches, and cannot be used to make comparisons among systems that use different lens systems and sensor sizes. Consequently, the traditional "magnification," which is decoupled from sensor resolution, is still the best way of describing the macro power of a lens, even though the user must factor in the sensor size and resolution.

this is a really good artical i used it to study my science i just wanted to point out to you that tere are a few spelling errors but other than that it is a 100% rating from me

The optical parts of the microscope are used to view, magnify, and produce an image from a specimen placed on a slide. These parts include: