While the simplest of microscopes is simply a magnifying glass with a single lens, compound microscopes used today are highly complex devices with a carefully designed series of lenses, filters, polarizers, beamsplitters, sensors, and perhaps even illumination sources. The exact combination of optical components used will depend on the application of the microscope; the wavelength of light with which it is intended to be used, and the resolution and magnification required in the final image.

Since the objective is closest to the specimen being examined, it will relay a real image to the ocular lens. While doing so, it contributes a base magnification of anywhere from 4x (for a scanning objective lens, typically used to provide an overview of a sample) to 100x (for oil immersion objectives).

Depth of fieldphotography examples

This page partially uses JavaScript. This page may not operate normally when these functions are not supported by your browser or the setting is disabled. Please look for the information you need from the following pages:

However, if the optical magnification of a lens differs greatly at both ends of the depth of focus, the front and rear depths of field are not equal as described in 3 and 4 above. Equations for the depth of field are presented in the following subsections. In the case of machine vision and other applications requiring relatively close focusing, we recommend using an equation with an optical magnification term. Otherwise, we recommend using an equation with a subject distance term.

For a detailed description of the depth of field, see Basics of camera lenses: Guidelines for lens selection and Consideration for depth of field in machine vision on our website. This section provides an overview of the depth of field and some added information about it.

At Shanghai Optics, we design and manufacture custom objectives and imaging systems to support our customers’ needs in many industries, including medical, biomedical, machine version, scientific research, and metrology, etc. Taking the client’s budget and precision requirements into consideration, our experienced engineering team ensure that each design can be manufactured at a reasonable cost and the optical performance is being met based on fabrication, assembly, and alignment tolerance analysis.

When a lens is focused at H/n, H/(n-1) and H/(n+1) are the rear and front depths of field respectively.For example, a lens focused at H holds a depth of field from H/2 to infinity.As shown in the previous subsection, when a lens is focused at infinity, the rear depth of field is infinite, going slightly “over infinity,” while the front depth of field is H.Dividing a hyperfocal distance (H) by an integer (n) means that the focal point shifts along the optical axis by half the depth of focus (δ*Fe) times n in relation to the lens extension (x’) at infinity.

Most machine vision applications provide close focusing. The following table shows the consecutive depths of field for relatively close focusing under the same conditions as above.

Since indirect backlight illumination is generally more effective than direct illumination, most microscopes do not include an internal light source.  Instead, they rely on daylight or on background illumination such as a lightbulb. In brightfield illumination, also known as Koehler illumination, two convex lenses saturate the specimen with external light admitted from behind. These two lenses, the collector lens and condenser lens, work together to provide a bright, even, and constant light throughout the system: on the image plane as well as on the object plane.  This system of illumination is used in many compound microscopes, including student microscopes and those found in many research labs.

Shallowdepth of field

The depth of focus refers to the tolerance of placement of an image sensor in relation to the lens. The depth of focus is the conjugate of the depth of field. Since both the depth of field and the depth of focus are abbreviated as DoF, they are hereinafter referred to as DoFi and DoFo respectively for the sake of clarity.The depth of focus (DoFo) is the distance over which a sensor can be displaced along the optical axis while an object remains in acceptably sharp focus. DoFo can be calculated from the permissible circle of confusion (δ) and the effective f-number (Fe).

Many objectives are designed to be used with a cover glass. Using an incorrect coverslip thickness can greatly reduce the optical performance of a microscopy system.

Focusing at H/n (where n is an integer) causes the depth of field to extend from N/(n+1) to H/(n-1). A hyperfocal sequence is a sequence of N/n:

Many of the readers of this white paper might have had questions before about the depth of field (DoF) not only when using machine vision systems but also when taking photographs with ordinary cameras.The depth of field is the distance between the nearest and the farthest objects in an image that appear acceptably sharp. You can find information about the depth of field on the Internet, in off-the-shelf books, and in trade journals. White papers about the depth of field are also available on our website under the headings Basics of camera lenses: Guidelines for lens selection and Consideration for depth of field in machine vision. These white papers discuss the depth of field from a different perspective than the commonly adopted one in the photography industry.This white paper describes, in an easy-to-understand way, the depth of field in relation to the hyperfocal distance and the hyperfocal sequence. Although these lens properties are closely related to each other, it is difficult to find such information on the Internet. Therefore, you will find this white paper useful.

Depths of focus are arranged as a sequence to show the ranges over which an object remains in acceptably sharp focus. This sequence is called a hyperfocal sequence (HS) or consecutive depths of focus.

F number depth of fieldcalculator

Alpha Industrial Park, Tu Thon Village, Ly Thuong Kiet Commune, Yen My District, Hung Yen Province Vietnam 17721 +84 221-730-8668 rfqvn@shanghai-optics.com

The following shows an equation for calculating the depth of field using the distance to a subject (x) from the focal point.Newton’s lens formula uses the front focal point as an origin to measure the distance to a subject (x). For typical shooting, a point on the opposite side of an image takes a negative value.The front depth of field (DoFN) is positive whereas the rear depth of field (DoFF) is negative. Since the total depth of field represents a distance, it is expressed as an absolute value.As effective f-numbers, the values calculated from the optical magnification at the front and rear depths of focus (FeN and FeF) are used. For general applications, FeN and FeF can be replaced with the Fe value that is calculated from optical magnification at a distance to the subject (x).

From Newton’s lens formula, the lens extension (x’) is expressed as follows using the camera-to-subject distance (x): The lens extensions (xN’ and xF’) at the nearest point of the front rear depth of field (DoFN) and the farthest point of the rear depth of field (DoFF) are calculated as follows using the effective f-number at x, Fex (denoted as Fe in the above paragraph): The linear magnification factors (βN and βF) and the effective f-numbers (FeN and FeF) at xN’ and xF’ are calculated as follows:

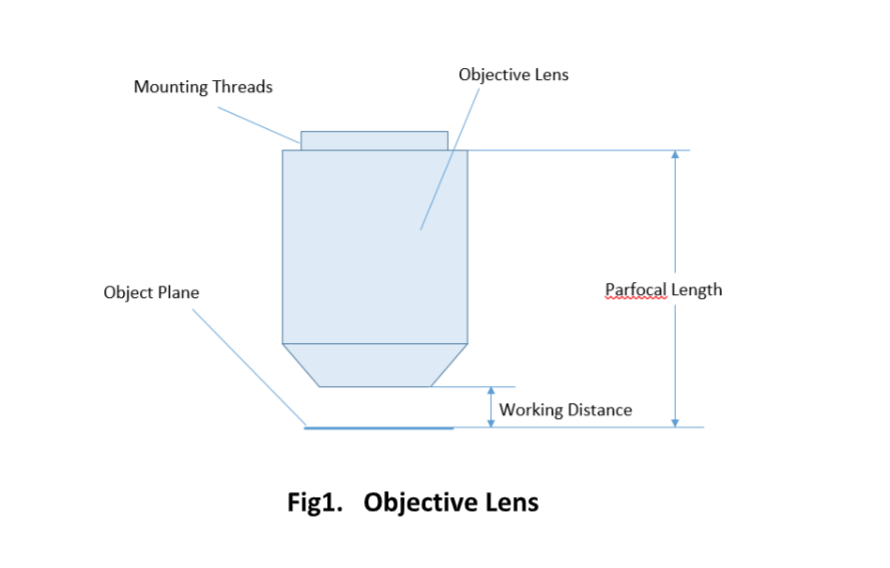
For keeping the objective at the proper position, there are mounting threads on almost all objectives. Commonly used mounting threads include RMS, M25 x 0.75, M26X 0.706, M32 x 0.75.

In order to determine the depth of focus (DoFo) accurately, it is necessary to consider the optical aberrations of a lens such as an image plane curvature. However, since such accuracy is generally unnecessary, the depth of focus is calculated based only on parameters along the optical axis.The DoFo value obtained by the above equation represents the most stringent case in terms of accuracy. For actual applications, a more relaxed value can be used as necessary. (For details, see the white paper Consideration for depth of field in machine vision from Toshiba Teli.)

The permissible circle of confusion (δ) is the larger of the pixel pitch (Ppix) and the diameter of the Airy disk (DAiry). So, let us calculate DAiry to determine δ:

Depth offocus

F number depth of fieldphotography

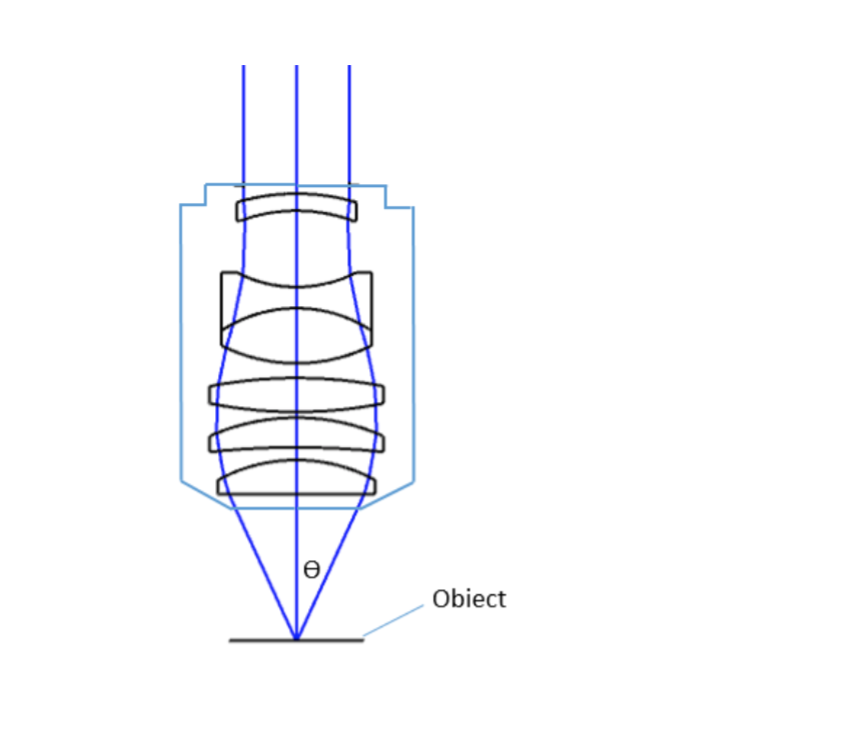
Most objectives are designed to image specimens with air as the medium between the objective and the cover glass. However, for achieving higher working numerical apertures, some objectives are designed to image the specimen through another medium such as special oil with a refractive index of 1.51.

Objectives are complex multi-element lenses. For any given application, careful consideration of the optical parameters and specifications is necessary. In many cases, custom-designed objective assemblies provide the best-fit solution for meeting all the requirements of a specialized application.  Custom parameters may include antireflection coatings, chromatic focus shift, working distance, image quality (MTF and spot size), lens mount, glass window thickness, and field of view, among others.

Important specifications are marked on the barrel of the objective, so students or researchers can easily identify the properties of an objective and determine the optical performance and working conditions for proper use. Figure 1 shows a diagram of an objective lens. A detailed discussion of the objection specifications is provided below.

Nowadays, surveillance cameras in distant-view shooting mode employ image shooting and processing techniques for machine vision cameras, for example, to synchronize trigger control with lighting.Suppose, for example, a wavelength of 550 nm, a camera with a pixel pitch of 3.45 μm, and an F2 lens with a focal length (f) of 50 mm. Let us calculate consecutive depths of field under these conditions.The specifications for the camera and the lens are:

Two optical systems provide the same depth of field when their lenses have the same optical magnification and f-number and their image sensors have the same pixel pitch.

F number depth of fieldcanon

Each microscope objective is itself a complex assembly of lenses, and besides contributing to the magnification, it is the objective lens which determines the resolution power of the microscope. An objective lens can also provide optical aberration corrections.  A reflective objective, for instance, includes two mirrors within the assembly. These mirrors can focus laser light as well as provide chromatic corrections.

Many machine vision applications shoot subjects at close distances (for example, at a distance of 300 mm). For close-up shooting, the depth of field can be calculated using optical magnification. The previous subsection explained the depth of field in relation to longitudinal magnification (α). The following shows an equation for calculating the depth of field using linear magnification, β (also called lateral or transverse magnification) since optical magnification generally means linear magnification. α and β have the following relationship: α=β2.

Magnification is one important parameter. Magnification is usually denoted by an X next to a numeric value.  Objectives are available in a range of magnifications from 2X to 200X.

A microscope objective is an important component of a microscopy or imaging system for a range of science research, biological, industrial, and general lab applications.. An objective lens determines the basic performance of an optical microscope or imaging systems and is designed for various performance needs and applications. It is located closest to the object and is an important component in imaging an object onto the human eye or an image sensor.

In this case also, focusing at H/n causes the depth of field to extend from H/(n+1) to H/(n-1). As you see, close focusing causes the depths of field to become considerably shallower than infinity focusing.In the case of close focusing with large optical magnification, the depth-of-field values differ considerably from the results of the calculation shown in Section 2.4. It is therefore recommended to consider the above depth-of-field values as rough estimates at an early stage of system design.

The parfocal length is the distance between the objective mounting plane and the specimen / object. This is another specification that can often vary by manufacturer.

The optical aberration correction determines the optical performance of an objective lens and plays a central role in the image quality and measurement accuracy of imaging or microscopy systems. According to the degrees of the aberration corrections, objective lenses are generally classified into five basic types: Achromat, Plan Achromat, Plan Fluorite (Plan Semi-Apochromat), Plan Apochromat, and Super Apochromat.

The ocular lens, or eyepiece, is also an optical assembly rather than a single lens, but it is typically more simple than the objective. Often it is composed of two lenses: a field lens and an eye lens. The design of the ocular lens determines the field of view of the microscope, as well as contributing to the total magnification of the system.

F number depth of fieldnikon

An image of a point source that is not in perfect focus appears as a blur spot called a circle of confusion (CoC). The size of the smallest spot that an image sensor cannot recognize as a blur is called the permissible circle of confusion or simply a circle of confusion.Even today when digital cameras are the mainstream cameras, the CoC diameters (δ) commonly referenced on the Internet (e.g., 0.033 mm, or 1/1300th of the image diagonal) are for images on silver halide films. These values are specified for images that are printed on a photographic paper of a certain size and viewed at a certain distance. In machine vision, which processes each pixel of an image sensor at high brightness levels, the permissible circle of confusion (δ) is calculated based on the pixel pitch (Ppix) or the diameter of the Airy disk (DAiry) that represents a limit to the optical resolution of an image created by a lens. In the case of monochrome cameras, the larger of these values is used as δ. (For color cameras with an on-chip color Bayer array filter, a value equal to two to three times δ is generally used.)

he depth of field is the distance between the nearest and the farthest objects in an image that appear acceptably sharp.When you shoot images, you focus a camera on objects at arbitrary distances. The distance to the nearest point in acceptably sharp focus in front of the best-focused point is called the front depth of field whereas the distance to the farthest point in acceptably sharp focus behind the best-focused point is called the rear depth of field. The distance between these points is the total depth of field.The depth of field can be calculated as described in the following subsection. However, objects appear differently, depending on their size and surface characteristics as well as the optical aberrations of the lens used. Therefore, cameras do not always come into sharp focus precisely at the calculated threshold; rather, they gradually come into and out of focus around a threshold.

These are all true, but this information does not help you determine which lens provides a greater depth of field because cameras with different sensor sizes require lenses with different focal lengths to obtain the same angle of view.Note that the depth of field is related to optical magnification. In the case of machine vision applications requiring close focusing at relatively high magnification, it would be safe to consider as follows:

Objective lenses can be classified based on the objective construction, field of use, microscopy method, performance (optical aberration corrections), and magnification. Many microscope objective manufacturers offer a wide range of objective designs, which provide various degrees of optical aberration corrections for supporting different needs. Mirrors or reflective elements are used in objective lenses for the applications that requires chromatic aberration over board spectral ranges. Most traditional microscopy systems use refractive objectives such as achromatic objectives (the cheaper objectives) for laboratory microscope applications and plan apochromats (expensive objectives) for biological and science research microscope applications.

Two major lens components—the objective lens and the ocular lens, or eyepiece—work together to project the image of the specimen onto a sensor. This may be the human eye or a digital sensor, depending on the microscope setup.

Microscope Objectives or Objective lenses are in many ways the heart of the microscope, and are typically mounted on a rotating nosepiece or turret to enable easy selection. Many microscopes will be equipped with a scanning objective (4x), a low power objective (10x), a high power objective (40x), and perhaps even an oil immersion objective lens.

Remember that the previous subsection mentioned that the depth of focus is the conjugate of the depth of field. A change in the object-side depth of focus caused by a displacement of the image plane by half the depth of focus is equal to half the depth of field. A slight displacement of an image plane causes the object-side focal point to shift by as much as a change in the image-side depth of focus divided by the longitudinal magnification of the lens. Because the depth of focus is symmetrical around the image plane, the depth of field is also symmetrical around the image plane.

A microscope is a special optical device designed to magnify the image of an object. Depending on the type of microscope, it may project the image either onto a human eye or onto a recording or video device. As an example, consider the photographs of cells that can be found in a science textbook. These photographs have all been taken by a specialized microscope, and may be called micrographs.

Depth of fieldcalculator

When a lens is focused at a hyperfocal distance (H) of about 362.3 m, the depth of field extends from infinity to H/2. So, the farthest point is infinity, and the nearest point is roughly 181.2 m. When the lens is focused at H/3 (≈120.8 m), the depth of field extends from about 181.2 m to about 90.6 m.

A simple magnifier (magnifying glass), works when the object to be examined is situated within focal length of the magnifier lens, enabling larger virtual image is produced. This type of magnifier is very limited in both resolution and magnification. A compound microscope, on the other hand, uses a relay lens system instead of the single lens, and since each lens component can contribute magnifying power, the result is greatly increased capability.

where θ is the maximum 1/2 acceptance ray angle of the objective, and n is the index of refraction of the immersion medium. Figure 2 shows the ray angle θ of an infinity-corrected objective.

Whens a lens is focused at infinity (x=∞, x’=0), the hyperfocal distance is equal to the front depth of field as given by the following equation. (Here, we use Newton’s lens formula since our attention is on the lens extension, x’.)Optical magnification has not been determined yet when you calculate a hyperfocal distance. Therefore, we use the f-number (F) at infinity (that is not modified by optical magnification) instead of the effective f-number (Fe).

Field of View is the area of the object that can be imaged by a microscopy system. The size of the field of view is determined by the objective magnification or focal length of the tube lens for an infinite-corrected objective. In a camera system, the field of view of the objective is related to the sensor size.

Gauss’ lens formula (1/(-a)+1/b=1/f) expresses the depth of field using the distance to a subject from the principal point.The subject distance used in Gauss’ lens formula is greater than the one used in Newton’s lens formula by the focal length of a lens (f). Therefore, the depth of field can be easily obtained simply by replacing x in Newton’s lens formula with a+f.The origin of the coordinate system for the subject distance (a) is the front principal point. For typical shooting, a point on the opposite side of an image takes a negative value.

The hyperfocal sequence is a sequence of successive H/n values, where n is an integer. The following table shows the values of H to H/5.(The unit of measure is mm. The negative sign that represents a direction is omitted.)

Room 609, 6/F, Global Gateway Tower, No.63 Wing Hong Street, Cheung Sha Wan, Kowloon, Hong Kong +852-54993705 info@shanghai-optics.com

The ocular lens, located at the top of a standard microscope and close to the sensor (receiving eye) receives the real image from the ocular lens, magnifies the image received and relays a virtual image to the sensor. While most eyepieces magnify 10x, there are some which provide no magnification and others which magnify as much as 30x. The magnification power of the microscope can be calculated by multiplying the magnification power of the eyepiece, or ocular lens, by the magnification power of the objective lens. For example, an objective lens with a magnification of 10x used in combination with a standard eyepiece (magnification 10x) would project an image of the specimen magnified 100x.

When a lens is focused on an object at a distance of H, a depth of field extends from infinity to H/2. In this case, H is called a hyperfocal distance.