What isobjective lens in microscope

iBiology and iBiology Courses are part of the Science Communication Lab (SCL). Our mission remains the same, to connect people to science. However, our focus has shifted to producing and evaluating cinematic films for education and the public, which you can find on the Science Communication Lab website. For more information, please see this blog post!

Objective and eyepiece lensof telescope

Room 609, 6/F, Global Gateway Tower, No.63 Wing Hong Street, Cheung Sha Wan, Kowloon, Hong Kong +852-54993705 info@shanghai-optics.com

Do not hesitate to contact Shanghai Optics today. We’d be more than happy to discuss your projects and how best they can become a success.

Alpha Industrial Park, Tu Thon Village, Ly Thuong Kiet Commune, Yen My District, Hung Yen Province Vietnam 17721 +84 221-730-8668 rfqvn@shanghai-optics.com

Objective lens microscopefunction

Microscope lenses are highly complex optical elements that correct for many different optical aberrations. This lecture describes a number of these aberrations and discusses what you should consider when selecting objective lenses as well as other precautions you can take to reduce the effects of aberrations.

Stephen Ross is the General Manager of Product and Marketing at Nikon Instruments.  He is also very involved in teaching microscopy at the Marine Biological Laboratory in Woods Hole and at the Bangalore Microscopy Course at the National Centre for Biological Sciences. Continue Reading

Objective lens and eyepiece lensfocal length

Shanghai Optics utilizes ImageMaster® TriOptics MTF Stations in-house for MTF testing, offering unparalleled accuracy and flexibility. These stations are equipped to handle various parameters and can measure MTF for both lens components and optical assemblies. MTF testing data is provided for optical systems and components upon request, enhancing the overall service offering.

This material is based upon work supported by the National Science Foundation and the National Institute of General Medical Sciences under Grant No. 2122350 and 1 R25 GM139147. Any opinion, finding, conclusion, or recommendation expressed in these videos are solely those of the speakers and do not necessarily represent the views of the Science Communication Lab/iBiology, the National Science Foundation, the National Institutes of Health, or other Science Communication Lab funders. © 2024-2006 by the Science Communication Lab · All content under CC BY-NC-ND 3.0 license · Privacy Policy · Terms of Use · Usage Policy

eyepiece and objective lens= total magnification

MTF plots and tables provide a visual representation of the testing results. Shanghai Optics showcases the MTF measurements of a 20X customized objective lens, demonstrating its design and manufacturing capabilities. The results depict MTF measured from 100lp/mm to 400lp/mm in both tangential and sagittal directions, highlighting the lens’s performance across different spatial frequencies.

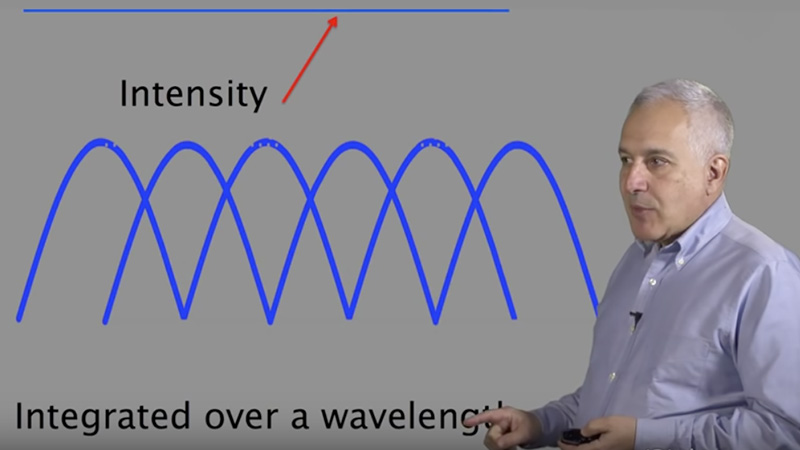
00:00:11.16 Hi, so in previous lectures we covered in general 00:00:16.06 the principles of lenses and how you form an image, 00:00:20.11 and how lenses are used in microscopy or microscope 00:00:23.27 instruments. I'm going to go into a little more detail 00:00:26.19 today, as to what really is specifically different about 00:00:32.29 an objective lens. I'm going to cover some of the types of 00:00:35.18 objective lenses and some of the properties that are important. 00:00:38.28 Mostly, I'm going to go through aberrations, optical 00:00:42.00 aberrations. And I'll talk, in general, about optical aberrations, 00:00:45.23 but I'll really concentrate more on the optical aberrations 00:00:50.11 that can become serious issues in the use of a research 00:00:55.15 microscope. I'm going to specifically talk about aberrations that 00:00:59.13 you can induce, that cannot be corrected in the designer 00:01:04.01 lenses. So let's just jump into it. I'm going to talk 00:01:06.04 in general about classes of objective lenses. And I have 00:01:09.19 three lenses here, and what you can notice right away 00:01:12.00 is that there's a very significant difference in the number of 00:01:17.17 lenses. So when we talked about lenses earlier in the lectures, 00:01:21.03 we talked about an ideal simple lens. And a lot of that is to allow us 00:01:26.02 to sort of grasp the principles at work. An objective lens is actually 00:01:32.07 the most complex optics in the system. And they actually are very 00:01:37.24 complicated lens groups within an objective, having anywhere 00:01:41.16 from 4 or 5 lenses in the simple achromat, all the way on the 00:01:45.05 far side there. To up to 17 lenses in a very highly corrected 00:01:50.15 plan apochromat lens. So there's a lot of tradeoffs that have to be 00:01:55.19 made. Mostly what you're doing with a lens, of course you 00:01:58.27 do magnify your image, in general, but what you're really doing is 00:02:04.17 making aberration corrections. You're concentrating on specific 00:02:08.12 transmissions, which is often specific to the type of research you're doing. 00:02:11.29 As well as you're resolving power, and resolving power is one of 00:02:16.28 the really key parts of a microscope objective lens. 00:02:21.01 So these three classes that I showed you here. We'll start with the 00:02:24.16 achromat lenses. Those are the lowest cost lenses 00:02:28.17 and the least corrected lenses. And you can see up here on the 00:02:31.19 top, the specifications of an achromat lens. Generally corrected 00:02:35.29 for red and blue, in around the 656 nm and 486 nm range. 00:02:42.12 And they correct for spherical aberration for one wavelength 00:02:46.12 in the green. Fluorite lenses are more highly corrected, and 00:02:50.03 they're corrected from 2-4 colors, for both axial chromatic aberration 00:02:56.02 and spherical aberration, which we're going to talk about later. 00:02:59.24 And the most highly corrected lenses are the apochromats. 00:03:03.20 Which are corrected for 4-5 colors, generally from the violet 00:03:06.20 out until the red. And those lenses are generally the more 00:03:13.18 expensive lenses. But not necessarily the best for the work that you're 00:03:16.29 trying to do. The more glass you put into a lens, the higher 00:03:21.04 the corrections are, the more transmission you lose. The more light 00:03:25.17 is absorbed by the glass. So it's always a tradeoff of corrections 00:03:30.02 versus transmission, and so on. And numerical aperature. 00:03:34.16 All of these types of lenses are available in what they call 00:03:37.12 Plan versions, which are flat-field corrected. So that when you look 00:03:42.14 in the eyepiece, you can see a nice flat corrected field of 00:03:45.09 view. In the case of most cameras and confocals, you're not using 00:03:49.27 that outer part of the field of view. So again, it depends on what 00:03:52.21 your needs are in the laboratory. So one property I want to talk 00:03:57.18 about on a lens is actually the most expensive part of the lens, 00:04:02.00 and also is the definition of a couple of things. First is the 00:04:09.11 resolving power of the lens, and that's numerical aperature. 00:04:11.28 The highest resolving power is the highest numerical aperature, 00:04:16.14 but it's also the highest light gathering capability. So a lens that's got 00:04:20.08 a very high numerical aperture will also be very bright, 00:04:23.13 compared to a lens with a low numerical aperture. And you 00:04:26.20 can see the formula right here for numerical aperture, NA 00:04:30.15 equals n, the refractive index of the immersion media, times the 00:04:34.12 Sin of theta. And the Sin of theta is the broadness of the cone of 00:04:38.08 illumination that you see there, and basically that is the light 00:04:42.00 gathering capability of the lens. It's also the cone of illumination 00:04:46.12 that light can come out of the lens at, which becomes important 00:04:49.21 for applications like total internal reflection fluorescence. 00:04:52.06 Okay, so numerical aperture, I just wanted to show you here 00:04:58.09 sort of the tradeoff of working distance versus numerical 00:05:02.09 aperture. And basically, you can see these two cones of illumination 00:05:06.11 for a very high numerical aperture lens, such as this 100X 00:05:10.01 lens here. You can see that it's got a very short working distance. 00:05:15.10 It has to be very close to the specimen, whereas the 4X 00:05:18.13 lens, which has a relatively low numerical aperture, you see 00:05:22.00 that it's got a very far working distance. So there's again, another 00:05:26.12 tradeoff you have to think about in the lenses. Generally, 00:05:30.10 there is a tradeoff between numerical aperture and working 00:05:33.26 distance. Okay, so you notice that the symbol "n" for refractive 00:05:42.21 index was coded, and that's a very special part of the equation 00:05:48.17 and I wanted to discuss that in a little more detail. And this really relates to 00:05:52.16 immersion media. So in an objective lens, you can see on the 00:05:57.17 far left there, an air objective lens. And what you see is light coming 00:06:04.01 up through the glass and it's refracted, or bent, as it leaves 00:06:07.24 the high refractive index glass going into air. And unless you 00:06:12.11 have an extremely large lens, you end up losing light 00:06:17.05 that is bent out of the collectable region of the objective lens. 00:06:20.15 So when we use higher NA, refractive index immersion media, 00:06:27.22 we can then decrease the refraction out of the collectible 00:06:32.18 area of the lens, and get more light into the lens. So you see on the 00:06:36.19 example on the right, there's an oil immersion lens where you have 00:06:41.17 no refraction, or very little refraction, between the glass and oil 00:06:45.10 interface, allowing the lens itself to collect the maximum 00:06:50.22 amount of light, and the maximum resolution. So in the 00:06:55.15 formula for numerical aperture, when you're thinking about resolution, 00:07:00.09 you should definitely think about immersion media, and you 00:07:05.03 should be aware of two things. One is that the higher the numerical 00:07:09.29 aperture, the higher resolution, and to get very high numerical 00:07:14.26 apertures, you have to go to an immersion media lens. 00:07:18.00 And also, that the numerical aperture of the lens, if you do some 00:07:23.11 rearranging of the equation, you can see that the numerical 00:07:26.08 aperture can never exceed the refractive index of the immersion 00:07:30.17 media. So shown here on the bottom, you can see a typical 00:07:34.18 immersion lens has a refractive index oil of 1.515, the maximum 00:07:39.23 NA lenses that are available for oil immersion is about a 1.49. 00:07:44.03 That's about the highest resolving power lens you can 00:07:47.23 get, and that has the highest refractive index media that 00:07:54.06 they use for standard microscopy. In the case of a water 00:07:57.25 immersion lens, water with a refractive index of 1.33 can have a 00:08:02.04 maximum NA of up to 1.27. So most commonly around 00:08:06.19 1.2, there are lenses available with 1.25 and 1.27 NA. 00:08:11.11 So next we're going to move on and into optical aberrations. 00:08:16.11 The first one I'm going to talk about is considered an off axis 00:08:20.19 aberration, it's affected mostly by light, it's not going straight 00:08:23.25 through the optical path, but light that's coming on off axis. 00:08:28.05 And that's called field curvature, now field curvature basically 00:08:32.13 is due to the curved surfaces of lenses and how you would see it 00:08:37.09 in the microscope is that you can't get the entire field in focus 00:08:40.28 at the same time. Maybe at one focal point you'll have the center 00:08:44.11 in focus, at another focal point you'll have the periphery 00:08:46.21 in focus. But you can't get them in focus at the same time. 00:08:49.20 Basically, it'll make the specimen appear to have the curvature 00:08:53.09 of the lens surface, and we do correct that by adding additional 00:08:57.07 lens groups in the objective lens. It's impossible to completely correct for 00:09:02.25 field curvature at the very outer edges. And that's why microscopes 00:09:06.03 generally have a larger field than they can actually see through the 00:09:10.13 eyepieces or through any of the imaging devices. 00:09:14.13 So basically, you clip or cut the outer curved field, where the 00:09:19.28 lenses get a very steep curvature at the edges. 00:09:22.28 The next off axis aberration I'm going to talk about is 00:09:26.08 astigmatism, and astigmatism is basically a point source 00:09:32.04 of light that appears as a line and/or an ellipse. And when you go 00:09:37.08 through focus, it changes its directionality, it comes into focus 00:09:40.26 and then changes directionality the other way. And that is 00:09:44.16 an astigmatism. This is also due to lens manufacturing, it's 00:09:52.01 basically due to an asymmetry in the manufacturing of lenses. 00:09:56.05 It's something that in general isn't really an issue in lenses, unless 00:10:01.02 they've been dropped or damaged. Most high quality lenses don't 00:10:04.25 have any appreciable astigmatism. That's also similar for 00:10:09.13 coma. Coma is an uneven focus of light as it passes through 00:10:15.04 the periphery versus the axis of the lens. It's similar to spherical 00:10:19.14 aberration, which I'm going to talk about later, but it's really more 00:10:22.05 of a property for off axis illumination. And the light that's 00:10:26.13 passing through the center, as you can see on the far right, 00:10:28.22 goes to one zone far off in the periphery, and then light 00:10:33.21 through the peripheral areas goes into different zones. 00:10:38.22 It appears in the microscope as a streak or a comet almost, 00:10:44.02 a point of light that has a tail that streaks out towards the 00:10:47.14 periphery of the lens. So often due to misalignment in an 00:10:52.13 optical system, so if the lens is in good shape, what you're going 00:10:55.09 want to do if you 're seeing coma in the image, is you're going to 00:10:58.18 want to make sure that your microscope is completely 00:11:01.21 aligned or methodically aligned so that everything is on axis. 00:11:08.24 Okay, so now we're going to move into on axis aberrations. 00:11:15.07 And the one that I'm going to talk about first is spherical aberration. 00:11:19.20 Spherical aberration is one of the most serious aberrations you 00:11:25.15 have to deal with in a microscope. And this is one that we do correct 00:11:29.11 as we talked about earlier, but we have to correct for under a very 00:11:33.10 limited set of conditions that are not realistic for imaging. 00:11:37.09 And I'll get into some more detail and explain that, but this 00:11:41.10 is one that's generally induced by the use of the microscope 00:11:45.28 under the conditions that you need to answer the questions you're interested 00:11:52.01 in the lab. So what it is is uneven focus of monochromatic light 00:11:56.24 due to the curvature of lenses. The next one I'm going to talk 00:12:01.21 about in some detail is axial chromatic aberration. So I'm 00:12:04.22 going to go back in detail for both of these. Axial chromatic 00:12:08.08 aberration is an on axis aberration, and that's actually due to the 00:12:13.19 dispersion of light. So light, when it passes through a media, each 00:12:17.29 media has its own property of dispersion, and that is that each 00:12:22.11 wavelength of light when it hits that media has a specific refractive 00:12:26.19 index. So some light is bent more than others. In the case of 00:12:31.05 the simple ideal lens, the blue light is bent more and you can 00:12:35.24 see that the blue light focuses closer on the lens than the red light, 00:12:39.06 which focuses further out. And this is a serious problem, but it's something 00:12:44.16 that we can correct for within reason in the microscope. 00:12:49.08 However, as I mentioned earlier, I'm going to talk about 00:12:51.06 aberrations that can be induced. So even if you have a very highly 00:12:55.03 corrected lens, it's possible to go ahead and induce chromatic 00:12:59.01 aberration by using the lens under improper conditions. 00:13:03.01 So, one thing that I think that is important to understand 00:13:07.14 for all discussions on aberrations is the point spread function. 00:13:11.27 Because it's going to come back several times throughout the course. 00:13:15.27 And basically, what the point spread function is is the convolution 00:13:20.15 of the point source of light as it passes through the optical 00:13:25.23 system. So if you have a point source of light, say that example on the 00:13:30.07 far right, and you focus up and down, and you build a 3D 00:13:33.18 volume, and you look at this X-Z projection here. You can see that 00:13:38.08 the X-Z projection looks like a small hourglass. That's actually 00:13:42.11 the best case scenario. If the optical system is working perfectly, 00:13:46.18 and everything is aligned and you have great quality lenses, 00:13:48.28 a point of light comes out as a small hourglass. Ideally at the 00:13:53.00 limit of resolution of that optical system. It defines the convolution 00:13:57.14 of the optical system, and is also a really good way to go ahead 00:14:02.17 and evaluate any aberrations in the microscope system. 00:14:06.05 Generally shown as a 3D X-Z projection, as you can see there. 00:14:09.24 So going into a little more detail, axial chromatic aberration, as I mentioned 00:14:15.11 before, is due to the dispersion of light as it passes through 00:14:20.20 material. So what you can see here is that example of chromatic 00:14:25.14 aberration, and at the bottom, we have a lens group called an 00:14:29.11 achromatic doublet, and in the case of an achromatic doublet, 00:14:32.03 what they do is they have two different types of glass that are 00:14:35.23 sandwiched together, usually a concave and a convex lens 00:14:39.20 that are sandwiched together, and both of those types of glass have different 00:14:43.28 dispersion properties. And they're calculated to correct for different 00:14:48.24 types of -- different wavelengths of light that they focus on 00:14:53.18 the same place. So a simple achromatic doublet like you see here 00:14:56.25 now is correcting so that red, green, and blue light are all focusing 00:15:00.11 on the same place. But! If you have this lens and it's very well corrected, 00:15:08.24 you can easily cause or induce chromatic aberration. 00:15:13.23 So what you see here is a figure looking at a three color 00:15:18.04 sub resolution bead. And you can see that on the far left, 00:15:22.23 there's an immersion oil from Nikon, which matches the 00:15:26.18 Nikon lens that this was imaged with. In the center, is another 00:15:30.10 immersion oil, which is from API, now GE Healthcare. 00:15:36.04 And third is an immersion oil from Cargille, which is a company 00:15:40.23 that makes immersion media for optical imaging. In fact, they 00:15:45.03 actually make all three of these oils. And what you can see 00:15:48.12 here is that in the X-Y projection, there's no shift or no aberration. 00:15:56.03 But when you look axially, in the X-Z projection, now you can see 00:16:00.27 in the Nikon oil, you have no shift. But in the center, you see 00:16:04.09 the API oil, you have a -400 shift in the blue signal and a +200 nm 00:16:09.28 shift in the red signal. In the case of the Cargille oil, you have a 00:16:15.02 #ERROR!overlapping. Well, the reason why these are all different, this is 00:16:22.11 all immersion oil that have a 1.515 refractive index, but they 00:16:28.04 differ in their dispersion. So each manufacturer that makes lenses 00:16:32.08 matches the oil to the dispersion of the glass that they 00:16:36.12 use to manufacture the lenses. So if you're going to go 00:16:39.15 and use a non-commercial, an oil that doesn't come from the 00:16:44.03 manufacturer, and there are reasons you'd want to do that, 00:16:46.05 for example, to get oils that match your refractive index of 00:16:48.29 water or special oils for special fluorescence properties, you'd want to find 00:16:54.22 out from the manufacturer what their dispersion number is. 00:16:59.09 It's called an Abbe number, and that is the dispersion number of the 00:17:02.05 glass that they've used to make that lens. If you then call up a company 00:17:06.15 like Cargille and ask them to formulate or send you oil that matches 00:17:11.23 that dispersion property, you'll eliminate this induced chromatic 00:17:15.16 aberration. So next, going into more detail of spherical aberration. 00:17:20.07 So, in the case of spherical aberration, we saw some examples 00:17:26.18 earlier, and we talked about what's called an ideal thin lens. 00:17:30.14 And that's a lens where light passes through, and you can see here, 00:17:33.14 a culminating beam of light passing through this lens 00:17:36.20 and it focuses to a point called the focal point. At 1f or 00:17:40.17 focal length away from that lens. It's a nice neat little diagram 00:17:44.22 and it allows you to understand in general terms how a lens works. 00:17:48.19 The problem is that in reality, there's no such thing as an ideal 00:17:53.09 thin lens. Like many of the things that we learn when we're 00:17:57.09 young, they are greatly oversimplified so that we can grasp 00:18:00.14 the concepts. In reality, lenses are actually made from spheres 00:18:04.26 of glass or other optical materials. Generally in the case of 00:18:08.12 microscopes, it's glass. So what you're looking at here is actually the top 00:18:12.05 lenses of a 100X plan apo lens. And they're small balls of 00:18:16.05 glass that are polished, and you can see this polishing machine 00:18:19.17 here, there's a pad up there that goes down and it polishes 00:18:22.26 on top, there's a diamond slurry that runs through. 00:18:26.11 One of the things that I really noticed when I first saw this 00:18:29.10 process was also why lenses to this day are so expensive. 00:18:32.28 A very highly corrected and high numerical aperture lens 00:18:36.05 can cost as much as the microscope you're putting it on. 00:18:39.11 And the reason for that is because lenses today are still made primarily by 00:18:45.12 hand. So these little top lenses actually polish for several weeks 00:18:48.28 and you can see the ones on the center of the plate, versus 00:18:52.08 the ones on the outer edge of the plate would rotate 00:18:54.16 in a different speed than the polisher. So somebody opens 00:18:57.21 this up every 30 minutes and moves those balls to this position, 00:19:01.10 and vice versa. So basically, I just wanted to show that lenses are 00:19:06.01 made from balls of glass, and there's no such thing as an ideal 00:19:09.15 thin lens. This is another lens. This is the second lens down 00:19:13.16 in a plan apo 60X magnification objective. And you can see 00:19:18.12 that they're polished in a different way, they sit on a stick 00:19:22.11 with tar holding them, and they polish around and around. 00:19:24.26 But still, spherical surfaces or curved surfaces add volume. 00:19:31.09 Okay, so now that you have that situation where you have 00:19:35.16 a spherical surface and curve, you have light that actually is refracted 00:19:41.02 or bent from that curvature. So, how do you induce spherical 00:19:45.17 aberration? Well, most commonly, so lenses are corrected for 00:19:49.01 it, but most commonly, it's done by the imaging conditions, 00:19:52.13 such as incorrect coverslip thickness or mismatch of the 00:19:57.00 refractive index of the immersion media. And it's not as simple 00:20:00.25 as it sounds. It's not a matter of, for example, with chromatic 00:20:05.05 aberrations, just buying the right oil. And I'll explain that in some 00:20:08.09 more detail. So now you have this nice simple figure, and 00:20:13.13 no longer do you have that nice neat focal point, but you have light 00:20:16.14 that's bent or refracted when it hits the air-glass surface 00:20:19.23 here on the lens, and then it goes through the lens and it's 00:20:23.03 bent or refracted again, and you get some rays that focus 00:20:26.22 close to the lens, some rays that focus away. And you end up with 00:20:30.27 this tight waist in the middle, which is termed the circle of 00:20:34.13 least confusion. And that actually is the tight waist of the point 00:20:38.25 spread function that you're imaging. And basically, the light that 00:20:44.09 goes through the axis, called the paraxial focus, is going to focus 00:20:48.23 further away from the lens. The light that comes from the periphery 00:20:52.16 here, is going to focus closer to the lens. 00:20:58.11 So you no longer have that nice little point, and you end up with 00:21:02.10 this smear in the Z direction of your focal plans. 00:21:05.13 So how do you recognize spherical aberration? And this is also 00:21:09.23 you would correct a correction collar or adjust a correction collar. 00:21:12.29 What you want to do is focus up and down on the microscope, 00:21:16.05 so this shows you a focus through of a point source of light, 00:21:19.22 and what happens is when you focus up and down, if you have no 00:21:23.12 spherical aberration present, you get perfect symmetry 00:21:27.06 above and below that point of focus. 00:21:30.10 However, in the case of spherical aberration, you'll have 00:21:34.24 a terrible asymmetry, maybe rings of light on one side and 00:21:38.25 a diffuse haze on the other side. And basically, then to adjust 00:21:45.17 a correction collar, you would move that collar until you see 00:21:48.22 the best symmetry of the smallest resolvable thing in the 00:21:54.00 specimen. Ideally beads are a great specimen to look at 00:21:58.18 subdiffraction spots, but that's not always a luxury you have. 00:22:01.12 So try and find something in your specimen that looks like it's 00:22:04.27 at the limit of resolution, focus up and down, adjust that collar, and 00:22:08.05 stop when you get the best symmetry focusing up and down. 00:22:11.27 So as I mentioned before, modern objective lenses are extremely 00:22:17.00 complicated. And I'm going to explain to you basically why we 00:22:20.18 can't correct for spherical aberration when manufacturing the lens. 00:22:24.08 So, here's a cutaway of a plan apo 60X lens. And you can see that this 00:22:30.01 lens actually has 17 lenses inside it, it's a very complicated optical 00:22:34.07 system. And you see some of those achromatic doublets, 00:22:37.14 such as right here, and the achromatic doublet, you actually have 00:22:42.24 to calculate the two different types of dispersion with the wavelengths 00:22:46.03 to correct for a band of wavelengths. But then when we add another 00:22:50.21 achromatic doublet to go ahead and correct for a larger band of 00:22:54.03 wavelengths, that changes all of the calculations that I made for the first 00:22:57.27 achromatic doublet. So I guess the point I want to make is when you have 00:23:01.12 a very complex optical system here with 17 lenses in it, 00:23:05.12 the math gets extremely, extremely complicated. And you 00:23:10.12 have to have known parameters to be able to solve that math 00:23:13.21 at all. Why are they so complicated? Well they have to correct 00:23:17.07 for chromatic aberration, field curvature, spherical aberration, 00:23:19.29 coma, astigmatism. So, in order to correct for this, the one variable 00:23:25.11 that we really must know is the optical path length. 00:23:29.00 So when designing a complex lens, knowing the optical path 00:23:33.08 length under a specific set of conditions, we can go ahead 00:23:36.12 and calculate how to solve for all these aberrations. 00:23:39.01 The optical path length, defined right here, is simply the 00:23:42.19 physical length of every material in that optical system 00:23:47.03 times its refractive index, summed up through this entire lens, 00:23:52.09 through the immersion media, through the coverglass, 00:23:55.09 to the point in the specimen that you're imaging. 00:23:58.16 So, it's nice and simple when we're inside the lens, because we 00:24:05.25 know to an extremely high accuracy the thickness of each 00:24:09.29 element. We also know its refractive index all the way out to 00:24:14.12 several decimal places. However, immersion media is really 00:24:17.22 variable. If you get a bottle of immersion oil, it will have a refractive 00:24:20.26 index of 1.515, but if you look closely, you'll see that that refractive 00:24:25.07 index is only for a single wavelength of light and it's only at 23C, 00:24:30.20 if that's a standard immersion oil. So, immersion media actually 00:24:35.01 decreases its refractive index as it warms up. 00:24:38.24 So it's actually a variable. Coverglass is a variable, as well. 00:24:42.13 Coverglass that we typically use is 170 microns thick. 00:24:46.16 But if you go and actually measure the glass in a box of coverslips, 00:24:50.28 you'll see that there's a plus or minus 10% range of the thickness 00:24:55.06 of that coverglass. The biggest variable is really the specimen. 00:24:58.24 There's not a lot you can do to control for that, the specimen may have 00:25:03.06 very, very optically dense areas, with refractive indices approaching 00:25:08.00 1.4, such as pure protein. Or refractive indices down close to 00:25:14.23 that of water, at 1.33, average probably about 1.38. 00:25:19.03 So in the case of live cell imaging, you have many different refractive 00:25:22.28 indices, and they're moving all the time. 00:25:26.23 So when we actually design an objective lens, we have to make 00:25:32.10 certain assumptions to be able to solve that math. 00:25:36.05 So the parameters that they use to design a lens are 00:25:39.17 that you're only going to use one wavelength of green light, 00:25:42.06 you're only going to work at 23C, the coverglass is exactly 00:25:45.24 170 microns thick, and you will image only point sources 00:25:50.01 at the surface of that coverslip and never focus into the 00:25:53.29 specimen. And if we can make those assumptions, we can calculate 00:25:57.19 the formula to design these complicated lenses. However, in reality, 00:26:02.06 most people cannot work at those conditions. So we have to 00:26:06.17 understand the aberration to minimize it as much as possible. 00:26:08.26 So how serious a problem is this? Well, if you look, there's that 00:26:13.22 perfect little point spread function on the top left there. 00:26:17.14 And that's right at the surface of the coverslip. When we go just 00:26:20.20 2 microns into the cell, the middle panel there on the top, 00:26:23.21 you now look like a small bulbous rocketship. 10um in, 00:26:28.21 on the bottom far left, it looks like a long stretched rocketship. 00:26:33.15 So imagine you're imaging, and every point in your specimen 00:26:36.11 looks like this spread out rocketship, with these streaking 00:26:40.05 tails coming down from it. Basically, that's going to decrease 00:26:43.26 the signal where your specimen actually is and give you a 00:26:47.01 diffuse background. That's why spherical aberration, many people 00:26:50.10 hear the word "spherical," and they think it's a curvature. 00:26:52.19 But in reality, spherical aberration, when you look in the 00:26:55.13 microscope, looks like a softness or a haziness in the image. 00:26:59.02 And it's one of those things where you're looking in the microscope, 00:27:01.19 and you keep going through focus and you're trying to focus 00:27:05.08 on the specimen, but it never really becomes sharp or crisp. 00:27:08.23 That's generally spherical aberration, there's nothing wrong with the 00:27:12.07 microscope, you just have an issue that you need to deal with. 00:27:15.15 So how do we correct for spherical aberration? We're going to have 00:27:22.14 another tip that'll go into some detail about that. But in general, 00:27:26.27 you try to work closely to those design criteria, or you use 00:27:31.05 objectives that have correction collars in them. 00:27:34.05 But how does a correction collar work? Generally what we'll do is 00:27:38.27 we'll look in the lens ray trace and look for the area in the lens, 00:27:43.15 which you can see all the way up front here, where you have the 00:27:47.02 steepest angle between two lens groups. So we would take all of 00:27:50.15 these lenses back here and put them in a brass tube, we would 00:27:54.15 score a groove around that tube, put a pin in it and connect it 00:27:57.28 a collar to that, then we would fix the other lenses in the front of 00:28:02.04 that angle in another brass tube. And when we turn that collar, 00:28:05.13 it moves all of these lenses back and forth, and then this 00:28:10.00 angle, up here, this steep angle, is then going to go like this 00:28:13.24 as those lenses move back and forth. So what happens 00:28:17.08 is, the axial rays that are focusing further away are now 00:28:23.15 brought into focus with the peripheral rays, because we're moving those 00:28:27.08 peripheral rays much more significantly than we're moving those 00:28:30.19 axial rays. And that's basically how a correction collar works. 00:28:33.24 So here's just a few images that show you spherical aberration. 00:28:38.23 Here's a three color image of fluorescence labeled cell. And you can see 00:28:44.16 actin labeled in green, and you can see mitochondria in red, and 00:28:50.14 DNA in the nucleus in blue. And you can resolve all of these structures 00:28:54.28 and you can even see some structure in the nucleus. But it 00:28:57.25 looks hazy, it looks soft. If we go ahead and correct for 00:29:00.29 spherical aberration, now you see the contrast just jumps 00:29:04.08 out. And it really can make a big difference in your imaging, 00:29:07.27 it can actually make the difference between seeing what you're interested 00:29:10.18 in or not. Here's another specimen, and this is one that we've worked with 00:29:15.10 in the lab for resolution test specimen. And this is a diatom. 00:29:19.12 And the surface spicules on this diatom are a good test 00:29:23.22 specimen, because they're right at the limit of resolution of 00:29:26.22 the optical microscope. And so you can see in this image, 00:29:30.17 with spherical aberration, it looks sort of soft or hazy, 00:29:33.05 but you go ahead and switch to correct for spherical 00:29:36.28 aberration and you can then really get a jump in contrast. 00:29:40.27 So that's all I have on optics and aberrations, thank you very much!

Objective lens and eyepiece lensmagnification

Modulation Transfer Function (MTF) stands as a pivotal metric in optics and image quality assessment. It provides a comprehensive evaluation of a lens system’s ability to reproduce spatial frequencies in an image accurately. At Shanghai Optics, MTF testing is conducted using state-of-the-art equipment, such as the ImageMaster® TriOptics MTF Stations, to ensure precise determination of imaging quality.

The MTF measurement process at Shanghai Optics involves a systematic approach using the ImageMaster® HR MTF station. The following steps outline the procedure:

MTF testing is a crucial aspect of Shanghai Optics’s optical manufacturing process, ensuring the highest standards of image quality. Through rigorous analysis, Shanghai Optics gains insights into the true capabilities of its lenses, guaranteeing superior contrast, sharpness, and resolution. This commitment to precision and quality underscores Shanghai Optics’s dedication to delivering optical solutions that excel in various industries, setting new standards for clarity and performance.