Optical Lenses Optical lenses work by refracting light rays. There are two main types of lens, "convex" and "concave". A convex lens will bring rays together. Its glass-in-air shape is (), i.e. it fatter at the middle than the edge. A concave lens has a "cave" or hollow. Its glass-in-air shape is )(, i.e. it is thinner at the middle than the edges. These are the four rays which you should be able to draw for a convex lens. 1 • Any ray through the centre of the lens will pass through undeviated. 2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

Example: A light ray is travelling in glass of refractive index, 1.5. It meets an interface with air (refractive index = 1.0) at an incident angle of 300. Find the angle of refraction.

Advanced Optics fabricates protected aluminum mirrors in almost any configuration from commercial grade down to 1/20 wave. For further information on how we can help you design the proper optical mirror for your application please visit our optical manufacturing capabilities page.

2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

[What would happen if there was no cladding around the core (n1=1) and you tried to find the incident light cone for transmission by total internal reflection?]

Total Internal Reflection When a light beam is directed along the axis of a cylindrical glass fibre, it reflects repeatedly off the edges of the fibre, without appreciable loss. This kind of reflection is called Total Internal Reflection. To explain how it arises, we need to look at the refraction which occurs when light, which is travelling in a medium with higher refractive index, hits an interface with a medium of lower refractive index. Example: A light ray is travelling in glass of refractive index, 1.5. It meets an interface with air (refractive index = 1.0) at an incident angle of 300. Find the angle of refraction. In general, when a light ray from a higher refractive index medium enters a lower refractive index medium, then the ray bends away from the normal. Critical Angle When a refracted angle equals 900 then a critical situation arises where the refracted ray travels along the interface. For typical glass with refractive index 1.5, this occurs when: For angles of incidence greater than the critical angle, the refracted ray does not exist, and the ray reflects off the interface at the same angle as it was incident. This reflection is called total internal reflection because there is no energy loss on reflection. The Silver reflecting surface in most domestic mirrors will absorb some of the incident light, so for them, multiple reflections will cause the image to fade away. Even though there is no energy loss in total internal reflection, the electric and magnetic fields of the light do penetrate a few wavelengths into the lower refractive medium. This wavelength penetration can be used to make variable-reflectance mirrors by placing another glass surface in near contact. This is known as frustrated total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. To couple light into optic fibres, the incoming light should be within a light cone that produces total internal reflection. This can be calculated by considering the geometry of the fibre core/envelope and the definition of the critical angle. Example: Calculate the largest angle of incidence available for light to be transmitted down an optic fibre which has core refractive index 1.50, and envelope refractive index 1.49. [What would happen if there was no cladding around the core (n1=1) and you tried to find the incident light cone for transmission by total internal reflection?] Optical Lenses Optical lenses work by refracting light rays. There are two main types of lens, "convex" and "concave". A convex lens will bring rays together. Its glass-in-air shape is (), i.e. it fatter at the middle than the edge. A concave lens has a "cave" or hollow. Its glass-in-air shape is )(, i.e. it is thinner at the middle than the edges. These are the four rays which you should be able to draw for a convex lens. 1 • Any ray through the centre of the lens will pass through undeviated. 2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

The DSX Series of opto-digital microscopes combines advanced optics and digital technology into one user-friendly system. Easy touch-screen control takes ...

Optical lenses work by refracting light rays. There are two main types of lens, "convex" and "concave". A convex lens will bring rays together. Its glass-in-air shape is (), i.e. it fatter at the middle than the edge. A concave lens has a "cave" or hollow. Its glass-in-air shape is )(, i.e. it is thinner at the middle than the edges.

Enhanced aluminum mirrors are overcoated with a thin dielectric layer that provides protection and durability to the fragile aluminum underneath, which otherwise should not be touched or wiped. Enhanced aluminum mirrors can be specifically tailored to improve reflectivity in either the UV or the visible spectrum, thereby extending their application range.

Advanced Optics fabricates protected silver mirrors in almost any configuration from commercial grade down to 1/20 wave. For further information on how we can help you design the proper optical mirror for your application please visit our optical manufacturing capabilities page.

5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

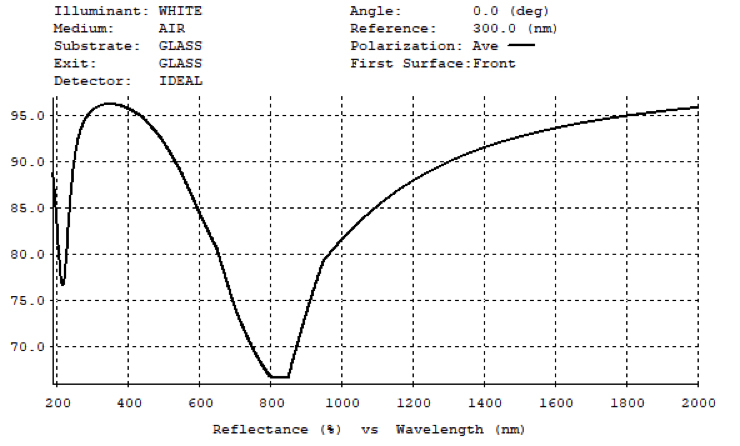
The disadvantage of this common, general-purpose coating is the dip in reflectivity at 880nm, which is due to the aluminum and enhanced by the overcoat. However, protected aluminum mirrors can be customized by centering the coating at a specific wavelength to maximize reflectivity where it matters most to your application. This makes protected aluminum mirrors not only economical but flexible enough to be used in a wide range of applications.

This can be calculated by considering the geometry of the fibre core/envelope and the definition of the critical angle. Example: Calculate the largest angle of incidence available for light to be transmitted down an optic fibre which has core refractive index 1.50, and envelope refractive index 1.49. [What would happen if there was no cladding around the core (n1=1) and you tried to find the incident light cone for transmission by total internal reflection?] Optical Lenses Optical lenses work by refracting light rays. There are two main types of lens, "convex" and "concave". A convex lens will bring rays together. Its glass-in-air shape is (), i.e. it fatter at the middle than the edge. A concave lens has a "cave" or hollow. Its glass-in-air shape is )(, i.e. it is thinner at the middle than the edges. These are the four rays which you should be able to draw for a convex lens. 1 • Any ray through the centre of the lens will pass through undeviated. 2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

To couple light into optic fibres, the incoming light should be within a light cone that produces total internal reflection. This can be calculated by considering the geometry of the fibre core/envelope and the definition of the critical angle. Example: Calculate the largest angle of incidence available for light to be transmitted down an optic fibre which has core refractive index 1.50, and envelope refractive index 1.49. [What would happen if there was no cladding around the core (n1=1) and you tried to find the incident light cone for transmission by total internal reflection?] Optical Lenses Optical lenses work by refracting light rays. There are two main types of lens, "convex" and "concave". A convex lens will bring rays together. Its glass-in-air shape is (), i.e. it fatter at the middle than the edge. A concave lens has a "cave" or hollow. Its glass-in-air shape is )(, i.e. it is thinner at the middle than the edges. These are the four rays which you should be able to draw for a convex lens. 1 • Any ray through the centre of the lens will pass through undeviated. 2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

Critical Angle When a refracted angle equals 900 then a critical situation arises where the refracted ray travels along the interface. For typical glass with refractive index 1.5, this occurs when: For angles of incidence greater than the critical angle, the refracted ray does not exist, and the ray reflects off the interface at the same angle as it was incident. This reflection is called total internal reflection because there is no energy loss on reflection. The Silver reflecting surface in most domestic mirrors will absorb some of the incident light, so for them, multiple reflections will cause the image to fade away. Even though there is no energy loss in total internal reflection, the electric and magnetic fields of the light do penetrate a few wavelengths into the lower refractive medium. This wavelength penetration can be used to make variable-reflectance mirrors by placing another glass surface in near contact. This is known as frustrated total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. To couple light into optic fibres, the incoming light should be within a light cone that produces total internal reflection. This can be calculated by considering the geometry of the fibre core/envelope and the definition of the critical angle. Example: Calculate the largest angle of incidence available for light to be transmitted down an optic fibre which has core refractive index 1.50, and envelope refractive index 1.49. [What would happen if there was no cladding around the core (n1=1) and you tried to find the incident light cone for transmission by total internal reflection?] Optical Lenses Optical lenses work by refracting light rays. There are two main types of lens, "convex" and "concave". A convex lens will bring rays together. Its glass-in-air shape is (), i.e. it fatter at the middle than the edge. A concave lens has a "cave" or hollow. Its glass-in-air shape is )(, i.e. it is thinner at the middle than the edges. These are the four rays which you should be able to draw for a convex lens. 1 • Any ray through the centre of the lens will pass through undeviated. 2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

For typical glass with refractive index 1.5, this occurs when: For angles of incidence greater than the critical angle, the refracted ray does not exist, and the ray reflects off the interface at the same angle as it was incident. This reflection is called total internal reflection because there is no energy loss on reflection. The Silver reflecting surface in most domestic mirrors will absorb some of the incident light, so for them, multiple reflections will cause the image to fade away. Even though there is no energy loss in total internal reflection, the electric and magnetic fields of the light do penetrate a few wavelengths into the lower refractive medium. This wavelength penetration can be used to make variable-reflectance mirrors by placing another glass surface in near contact. This is known as frustrated total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. To couple light into optic fibres, the incoming light should be within a light cone that produces total internal reflection. This can be calculated by considering the geometry of the fibre core/envelope and the definition of the critical angle. Example: Calculate the largest angle of incidence available for light to be transmitted down an optic fibre which has core refractive index 1.50, and envelope refractive index 1.49. [What would happen if there was no cladding around the core (n1=1) and you tried to find the incident light cone for transmission by total internal reflection?] Optical Lenses Optical lenses work by refracting light rays. There are two main types of lens, "convex" and "concave". A convex lens will bring rays together. Its glass-in-air shape is (), i.e. it fatter at the middle than the edge. A concave lens has a "cave" or hollow. Its glass-in-air shape is )(, i.e. it is thinner at the middle than the edges. These are the four rays which you should be able to draw for a convex lens. 1 • Any ray through the centre of the lens will pass through undeviated. 2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

Jun 5, 2024 — Barrel lens distortion is an effect associated with wide-angle lenses and, in particular, zoom wide-angles. This effect causes the image to ...

When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).

This kind of reflection is called Total Internal Reflection. To explain how it arises, we need to look at the refraction which occurs when light, which is travelling in a medium with higher refractive index, hits an interface with a medium of lower refractive index. Example: A light ray is travelling in glass of refractive index, 1.5. It meets an interface with air (refractive index = 1.0) at an incident angle of 300. Find the angle of refraction. In general, when a light ray from a higher refractive index medium enters a lower refractive index medium, then the ray bends away from the normal. Critical Angle When a refracted angle equals 900 then a critical situation arises where the refracted ray travels along the interface. For typical glass with refractive index 1.5, this occurs when: For angles of incidence greater than the critical angle, the refracted ray does not exist, and the ray reflects off the interface at the same angle as it was incident. This reflection is called total internal reflection because there is no energy loss on reflection. The Silver reflecting surface in most domestic mirrors will absorb some of the incident light, so for them, multiple reflections will cause the image to fade away. Even though there is no energy loss in total internal reflection, the electric and magnetic fields of the light do penetrate a few wavelengths into the lower refractive medium. This wavelength penetration can be used to make variable-reflectance mirrors by placing another glass surface in near contact. This is known as frustrated total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. To couple light into optic fibres, the incoming light should be within a light cone that produces total internal reflection. This can be calculated by considering the geometry of the fibre core/envelope and the definition of the critical angle. Example: Calculate the largest angle of incidence available for light to be transmitted down an optic fibre which has core refractive index 1.50, and envelope refractive index 1.49. [What would happen if there was no cladding around the core (n1=1) and you tried to find the incident light cone for transmission by total internal reflection?] Optical Lenses Optical lenses work by refracting light rays. There are two main types of lens, "convex" and "concave". A convex lens will bring rays together. Its glass-in-air shape is (), i.e. it fatter at the middle than the edge. A concave lens has a "cave" or hollow. Its glass-in-air shape is )(, i.e. it is thinner at the middle than the edges. These are the four rays which you should be able to draw for a convex lens. 1 • Any ray through the centre of the lens will pass through undeviated. 2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

4COATING FILM LENS: The 4X objective lens is coated, has high transmittance and refractive index, making it less prone to scratches, fragmentation, or wear. 5 ...

1 • Any ray through the centre of the lens will pass through undeviated. 2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

Example: Calculate the largest angle of incidence available for light to be transmitted down an optic fibre which has core refractive index 1.50, and envelope refractive index 1.49. [What would happen if there was no cladding around the core (n1=1) and you tried to find the incident light cone for transmission by total internal reflection?] Optical Lenses Optical lenses work by refracting light rays. There are two main types of lens, "convex" and "concave". A convex lens will bring rays together. Its glass-in-air shape is (), i.e. it fatter at the middle than the edge. A concave lens has a "cave" or hollow. Its glass-in-air shape is )(, i.e. it is thinner at the middle than the edges. These are the four rays which you should be able to draw for a convex lens. 1 • Any ray through the centre of the lens will pass through undeviated. 2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

In this lecture the following are introduced: • Total internal reflection • Optical fibres • Image formation by convex lenses • Image formation by concave lenses

When a light beam is directed along the axis of a cylindrical glass fibre, it reflects repeatedly off the edges of the fibre, without appreciable loss. This kind of reflection is called Total Internal Reflection. To explain how it arises, we need to look at the refraction which occurs when light, which is travelling in a medium with higher refractive index, hits an interface with a medium of lower refractive index. Example: A light ray is travelling in glass of refractive index, 1.5. It meets an interface with air (refractive index = 1.0) at an incident angle of 300. Find the angle of refraction. In general, when a light ray from a higher refractive index medium enters a lower refractive index medium, then the ray bends away from the normal. Critical Angle When a refracted angle equals 900 then a critical situation arises where the refracted ray travels along the interface. For typical glass with refractive index 1.5, this occurs when: For angles of incidence greater than the critical angle, the refracted ray does not exist, and the ray reflects off the interface at the same angle as it was incident. This reflection is called total internal reflection because there is no energy loss on reflection. The Silver reflecting surface in most domestic mirrors will absorb some of the incident light, so for them, multiple reflections will cause the image to fade away. Even though there is no energy loss in total internal reflection, the electric and magnetic fields of the light do penetrate a few wavelengths into the lower refractive medium. This wavelength penetration can be used to make variable-reflectance mirrors by placing another glass surface in near contact. This is known as frustrated total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. To couple light into optic fibres, the incoming light should be within a light cone that produces total internal reflection. This can be calculated by considering the geometry of the fibre core/envelope and the definition of the critical angle. Example: Calculate the largest angle of incidence available for light to be transmitted down an optic fibre which has core refractive index 1.50, and envelope refractive index 1.49. [What would happen if there was no cladding around the core (n1=1) and you tried to find the incident light cone for transmission by total internal reflection?] Optical Lenses Optical lenses work by refracting light rays. There are two main types of lens, "convex" and "concave". A convex lens will bring rays together. Its glass-in-air shape is (), i.e. it fatter at the middle than the edge. A concave lens has a "cave" or hollow. Its glass-in-air shape is )(, i.e. it is thinner at the middle than the edges. These are the four rays which you should be able to draw for a convex lens. 1 • Any ray through the centre of the lens will pass through undeviated. 2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

Protected aluminum is a popular choice in the visible spectrum due to its low cost and good reflectivity with Ravg >85% from 400 – 700nm. It continues to provide good reflectivity into the NIR spectrum with Ravg >90% 400 – 2000nm making it an excellent choice for many broadband applications.

Advanced Optics fabricates protected silver mirrors in almost any configuration from commercial grade down to 1/20 wave.  Please visit our optical manufacturing capabilities page for additional information

Metallic coated optical mirrors are coated with various metals to provide reflectivity across the UV, VIS, and IR spectra making them an excellent choice for a wide range of applications. When choosing a metallic coating, one should carefully consider the following:

Concave lenses have total internal reflectionquizlet

Advanced Optics can help you customize your protected gold coating to meet your reflectivity requirements. We fabricate protected gold mirrors in almost any configuration from commercial grade down to 1/20 wave. Please visit our optical manufacturing capabilities page to see how we can help you meet your requirements.

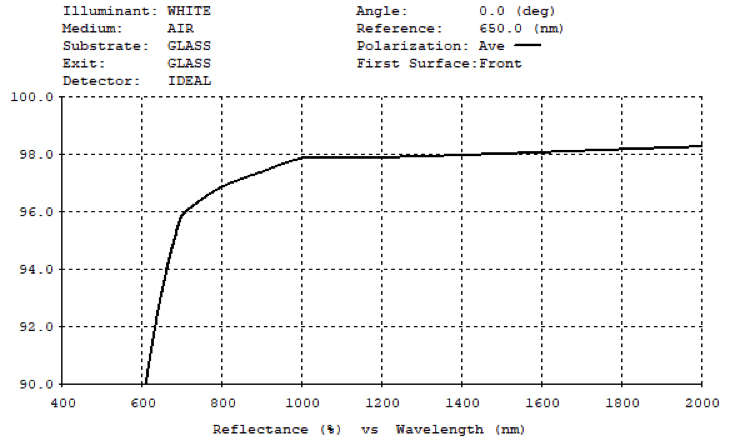
Protected gold mirrors have a thin dielectric overcoat that provides durability for the soft gold underneath, which otherwise should not be touched or cleaned. When your application requires high reflectivity in the NIR or IR spectrum, these mirrors excel with Ravg >96% from 700 – 2000nm and Ravg >98% from 2 - 10µm.

The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high.

Protected aluminum mirrors are coated with aluminum and a ½ wave of either silicon monoxide or silicon dioxide overcoat. The choice of overcoat may need to be considered due to the thermal implications of how each is applied and the wavelength of intended use. Either overcoat provides abrasion resistance for the soft aluminum underneath, which should otherwise not be touched or cleaned. The protective overcoat also keeps the aluminum from oxidizing over time.

8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane.

Advanced Optics manufactures optical mirrors that offer reflectivity from 190nm – 20µm. Please visit our technical bare (unprotected) metallic coatings page to learn more about mirrors without a protective overcoat.

VD Tang · 2023 — Focal length is the distance between the lens and the focal point, where the light rays converge or diverge.

The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

PCB Retainer C · Possible application on top and bottom horizontal rail · Can also be used without PCB handle · Can also be used from Slot position "2" · For ...

Concave lenses have total internal reflectionbrainly

Even though there is no energy loss in total internal reflection, the electric and magnetic fields of the light do penetrate a few wavelengths into the lower refractive medium. This wavelength penetration can be used to make variable-reflectance mirrors by placing another glass surface in near contact. This is known as frustrated total internal reflection.

Atomlaser: Experimente mit kohärenten Materiewellen. Applicant Professor Dr. Tilman Esslinger. Subject Area Optics, Quantum Optics and Physics of Atoms ...

Nov 20, 2006 — Click on a Telescope Below: 1) Mag 1 Instruments 8" Portaball 2) Edmund Scientific (Scientifics) Astroscan. 1) Mag 1 Instruments 8" Portaball ...

In addition to our standard UV enhanced aluminum coating, Advanced Optics offers a deep UV enhanced aluminum coating for use down to 190nm.

4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane.

From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object.

Silver can be enhanced to provide 99% reflectivity at a specific wavelength between 400nm – 20µm. However, the overall curve is not as flat as standard protected silver as illustrated in the curve below, which is optimized at 520nm.

The disadvantage of choosing a protected silver mirror is its propensity to oxidize over time. The protective dielectric overcoat is helpful but these mirrors will eventually tarnish, and environmental factors such as humidity will accelerate the process.

UV and DUV Enhanced Aluminum Mirrors Enhancing the aluminum in the UV spectrum provides Ravg >90% 250 – 450nm and Ravg >85% 250 – 700nm.

In general, when a light ray from a higher refractive index medium enters a lower refractive index medium, then the ray bends away from the normal. Critical Angle When a refracted angle equals 900 then a critical situation arises where the refracted ray travels along the interface. For typical glass with refractive index 1.5, this occurs when: For angles of incidence greater than the critical angle, the refracted ray does not exist, and the ray reflects off the interface at the same angle as it was incident. This reflection is called total internal reflection because there is no energy loss on reflection. The Silver reflecting surface in most domestic mirrors will absorb some of the incident light, so for them, multiple reflections will cause the image to fade away. Even though there is no energy loss in total internal reflection, the electric and magnetic fields of the light do penetrate a few wavelengths into the lower refractive medium. This wavelength penetration can be used to make variable-reflectance mirrors by placing another glass surface in near contact. This is known as frustrated total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. To couple light into optic fibres, the incoming light should be within a light cone that produces total internal reflection. This can be calculated by considering the geometry of the fibre core/envelope and the definition of the critical angle. Example: Calculate the largest angle of incidence available for light to be transmitted down an optic fibre which has core refractive index 1.50, and envelope refractive index 1.49. [What would happen if there was no cladding around the core (n1=1) and you tried to find the incident light cone for transmission by total internal reflection?] Optical Lenses Optical lenses work by refracting light rays. There are two main types of lens, "convex" and "concave". A convex lens will bring rays together. Its glass-in-air shape is (), i.e. it fatter at the middle than the edge. A concave lens has a "cave" or hollow. Its glass-in-air shape is )(, i.e. it is thinner at the middle than the edges. These are the four rays which you should be able to draw for a convex lens. 1 • Any ray through the centre of the lens will pass through undeviated. 2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

These half ball lenses offer a practical alternative to traditional optical ball lenses, especially in scenarios with space limitations. With their unique half ...

As with our standard protected aluminum coatings, Advanced Optics can design UV enhanced aluminum and visible spectrum enhanced aluminum coatings centered at a specific wavelength to maximize reflectivity in the area of the spectrum that matters most to your application. Advanced Optics fabricates enhanced aluminum mirrors in almost any configuration from commercial grade down to 1/20 wave. Please visit our optical manufacturing capabilities page to see how we can help you meet your requirements.

CW · chemical warfare. · Radio and Televisioncontinuous wave. · Abbreviationsconventional wisdom.

7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image.

Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

Peter's Physics Pages  Peter's Index   Physics Home   Lecture 7   Course Index   Lecture 9  An Introductory Physics Course with Peter Eyland Lecture 8 (Optical fibres & lenses)

3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. To couple light into optic fibres, the incoming light should be within a light cone that produces total internal reflection. This can be calculated by considering the geometry of the fibre core/envelope and the definition of the critical angle. Example: Calculate the largest angle of incidence available for light to be transmitted down an optic fibre which has core refractive index 1.50, and envelope refractive index 1.49. [What would happen if there was no cladding around the core (n1=1) and you tried to find the incident light cone for transmission by total internal reflection?] Optical Lenses Optical lenses work by refracting light rays. There are two main types of lens, "convex" and "concave". A convex lens will bring rays together. Its glass-in-air shape is (), i.e. it fatter at the middle than the edge. A concave lens has a "cave" or hollow. Its glass-in-air shape is )(, i.e. it is thinner at the middle than the edges. These are the four rays which you should be able to draw for a convex lens. 1 • Any ray through the centre of the lens will pass through undeviated. 2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

Who is ISP Optics. LightPath's wholly-owned subsidiary, ISP Optics Corporation, manufactures a full range of infrared products from high performance MWIR ...

The disadvantage of choosing a protected silver mirror is its propensity to oxidize over time. The protective dielectric overcoat is helpful but these mirrors will eventually tarnish, and environmental factors such as humidity will accelerate the process.

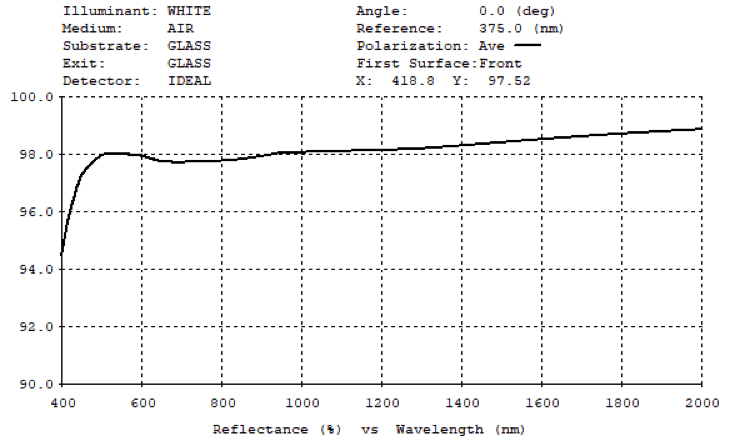
Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image.

When a refracted angle equals 900 then a critical situation arises where the refracted ray travels along the interface. For typical glass with refractive index 1.5, this occurs when: For angles of incidence greater than the critical angle, the refracted ray does not exist, and the ray reflects off the interface at the same angle as it was incident. This reflection is called total internal reflection because there is no energy loss on reflection. The Silver reflecting surface in most domestic mirrors will absorb some of the incident light, so for them, multiple reflections will cause the image to fade away. Even though there is no energy loss in total internal reflection, the electric and magnetic fields of the light do penetrate a few wavelengths into the lower refractive medium. This wavelength penetration can be used to make variable-reflectance mirrors by placing another glass surface in near contact. This is known as frustrated total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. To couple light into optic fibres, the incoming light should be within a light cone that produces total internal reflection. This can be calculated by considering the geometry of the fibre core/envelope and the definition of the critical angle. Example: Calculate the largest angle of incidence available for light to be transmitted down an optic fibre which has core refractive index 1.50, and envelope refractive index 1.49. [What would happen if there was no cladding around the core (n1=1) and you tried to find the incident light cone for transmission by total internal reflection?] Optical Lenses Optical lenses work by refracting light rays. There are two main types of lens, "convex" and "concave". A convex lens will bring rays together. Its glass-in-air shape is (), i.e. it fatter at the middle than the edge. A concave lens has a "cave" or hollow. Its glass-in-air shape is )(, i.e. it is thinner at the middle than the edges. These are the four rays which you should be able to draw for a convex lens. 1 • Any ray through the centre of the lens will pass through undeviated. 2 • Any ray diverging from the primary focal point will emerge parallel to the axis 3 • Any ray parallel to the axis will converge to the secondary focal point. 4 • Any ray will converge to that point in the secondary focal plane, where a parallel ray through the centre intersects with the focal plane. These are the four rays which you should be able to draw for a concave lens. 5 • Any ray through the centre of the lens will pass through undeviated. 6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

6 • Any ray parallel to the axis will diverge as if it came from the primary focal point. 7 • Any ray converging towards the secondary focal point will emerge parallel to the axis. 8 • Any ray will diverge from that point in the primary focal plane, where a parallel ray through the centre intersects with the focal plane. Image formation by a convex lens 1 • Object inside the focal length. the image is virtual, upright & enlarged. 2 • Object between the focal length and twice the focal length. The image is real, inverted & enlarged 3 • Object greater than twice focal length. The image is real, inverted & diminished Image formation by a concave lens 4 • Real object The image is virtual, upright & diminished 5 • Virtual object The image is real, upright & enlarged The lens formula From similar triangles:      Also from different similar triangles:     Example An object 30mm high is placed 300mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is real (v is positive), inverted (m is negative), and enlarged (m is greater than 1). It is 600mm behind the lens and 30 x 2.0 = 60mm high. Example An object 50mm high is placed 100mm in front of a 200mm convex lens. Find the position, size and nature of the image. The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high. Example An object is placed in front of a 120mm concave lens. The image is upright, 25mm high and -80mm from the lens. Find the position and size of the object. The object is real (u is positive), 240mm in front of the lens. Its size is 3x the image, i.e. 75mm high. Summarising: When light changes from a higher refractive index medium to a lower refractive index it bends away from the normal At the critical angle the refracted ray is at 900, i.e. parallel to the surface. and At incidence greater than the critical angle there is total internal reflection. Optical fibres have a protective envelope around them so that wavelength penetration does not produce any energy loss. Convex lenses are thicker at the middle than the edges. Concave lenses are thinner at the middle than the edges. There are four standard light paths for convex and concave lenses. The lens equations use the convention: real is positive (where minus means inverted).  Peter's Index   Physics Home   Lecture 7   top of page   Lecture 9  email Write me a note if you found this useful Copyright Peter & BJ Eyland. 2007 -2015 All Rights Reserved. Website designed and maintained by Eyland.com.au ABN79179540930. Last updated 17 January 2015

Calculate the largest angle of incidence available for light to be transmitted down an optic fibre which has core refractive index 1.50, and envelope refractive index 1.49.

The image is virtual (v is negative), upright (m is positive) and enlarged (m is greater than 1). It is 200mm in front of the lens and 50 x 2.0 = 100mm high.

Protected silver mirrors have a thin dielectric overcoat that provides durability and prevents the silver underneath from rapid oxidation. These mirrors offer higher reflectivity over a broader spectral range than aluminum coated mirrors with Ravg > 97.5% from 450 – 2000nm and Ravg > 98% from 2 – 20µm. This makes them ideal for applications that require high, fairly flat reflectivity over the visible and NIR spectrum.

For angles of incidence greater than the critical angle, the refracted ray does not exist, and the ray reflects off the interface at the same angle as it was incident. This reflection is called total internal reflection because there is no energy loss on reflection. The Silver reflecting surface in most domestic mirrors will absorb some of the incident light, so for them, multiple reflections will cause the image to fade away.