Quarter wave platematrix

The quarter wavelength retardation plate is designed to introduce a relative retardation of exactly one-quarter wavelength (in the green or 550 nanometer region), or 90 degrees, between the ordinary and extraordinary wavefronts passing through the plate when the birefringent retardation material is illuminated by linearly polarized light at a 45-degree incident angle to the index ellipsoid, as illustrated in Figure 2. The resulting phase shift converts the linear input wavefront to a circularly polarized output wavefront. This action occurs because the orthogonal ordinary and extraordinary components have equal amplitudes when linear light oriented at a 45-degree angle to the principal (the fast or slow) axes is incident on a quarter wavelength retardation plate. In a similar manner, the quarter wavelength plate will convert an incoming circularly polarized wavefront into a linearly polarized wavefront.

Where are diffraction gratings used in applications? Diffraction gratings are commonly used for spectroscopic dispersion and analysis of light. What makes them particularly useful is the fact that they form a sharper pattern than double slits do. That is, their bright fringes are narrower and brighter while their dark regions are darker. Diffraction gratings are key components of monochromators used, for example, in optical imaging of particular wavelengths from biological or medical samples. A diffraction grating can be chosen to specifically analyze a wavelength emitted by molecules in diseased cells in a biopsy sample or to help excite strategic molecules in the sample with a selected wavelength of light. Another vital use is in optical fiber technologies where fibers are designed to provide optimum performance at specific wavelengths. A range of diffraction gratings are available for selecting wavelengths for such use.

Commercial quarter wavelength retardation plates are specified by their linear retardation, which is 137 nanometers for the device illustrated in Figure 1 that is designed to operate in light having a principal wavelength of 548 nanometers (in the green region). In polarized light microscopy applications, the quarter wavelength plate is utilized in a similar manner to the full wave retardation plate in order to determine whether the combination of a weakly birefringent specimen and the plate (oriented at a 45-degree angle to the polarizer and analyzer) yield higher or lower order interference colors. However, the quarter wavelength plate has been largely supplanted by the full wave retardation plate due to the superior sensitivity of the latter in producing color changes that can be readily observed. In cases where birefringent specimens display higher order interference colors between crossed polarizers without a retardation plate, then the quarter wavelength plate can often be used to advantage over the full wave plate to determine optical path differences.

Quarter wave plateformula

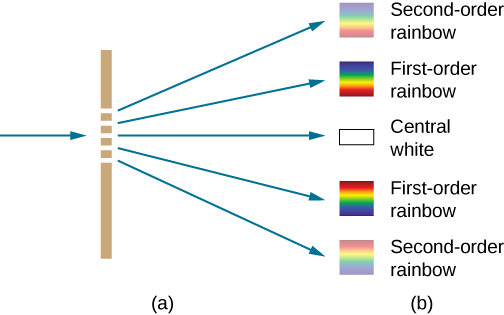
Take the same simulation we used for double-slit diffraction and try increasing the number of slits from to . The primary peaks become sharper, and the secondary peaks become less and less pronounced. By the time you reach the maximum number of , the system is behaving much like a diffraction grating.

Jones matrix

The analysis of multi-slit interference in Interference allows us to consider what happens when the number of slits N approaches infinity. Recall that secondary maxima appear between the principal maxima. We can see there will be an infinite number of secondary maxima that appear, and an infinite number of dark fringes between them. This makes the spacing between the fringes, and therefore the width of the maxima, infinitesimally small. Furthermore, because the intensity of the secondary maxima is proportional to , it approaches zero so that the secondary maxima are no longer seen. What remains are only the principal maxima, now very bright and very narrow ((Figure)).

The simple anatomy of a quarter wavelength retardation plate is presented in Figure 1 for a typical commercial unit. Retardation materials employed in construction of the plate vary according to the application, but usually consist of either an optical mineral thin section (such as quartz or mica) or a highly aligned birefringent linear organic polymer sandwiched between two isotropic optically flat glass plates. Regardless of the material used in producing retardation, the optical path difference (usually inscribed on the retardation plate frame) and optical axis orientation of the birefringent retarding material must be carefully controlled so that the plate can add a known retardation value to both the high and low refractive index azimuths of orthogonal wavefronts. As illustrated in Figure 1, the birefringent retardation material is positioned in the window of a rectangular frame that is inserted into the microscope optical pathway at a 45-degree angle with respect to the transmission orientations of the polarizer and analyzer. The direction of the slow (high refractive index) axis of the wavefront ellipsoid is indicated on the retardation plate frame as a double-headed arrow accompanied by the Greek symbol for "gamma" (γ). In most cases, the slow axis orientation is perpendicular to the long dimension of the retardation plate frame, although this fact should be verified before attempting to use the instrument. Modern quarter wavelength retardation plates are built in a frame having standardized DIN dimensions (6 × 20 millimeters) that will enable their use in a variety of microscopes.

What is the distance between lines on a diffraction grating that produces a second-order maximum for 760-nm red light at an angle of ?

Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.

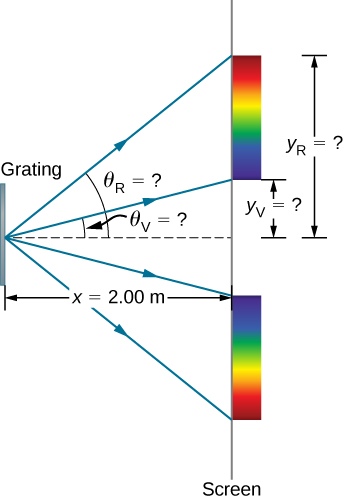
Since there are 10,000 lines per centimeter, each line is separated by 1/10,000 of a centimeter. Once we know the angles, we an find the distances along the screen by using simple trigonometry.

Significance The large distance between the red and violet ends of the rainbow produced from the white light indicates the potential this diffraction grating has as a spectroscopic tool. The more it can spread out the wavelengths (greater dispersion), the more detail can be seen in a spectrum. This depends on the quality of the diffraction grating—it must be very precisely made in addition to having closely spaced lines.

What is the spacing between structures in a feather that acts as a reflection grating, giving that they produce a first-order maximum for 525-nm light at a angle?

An electric current through hydrogen gas produces several distinct wavelengths of visible light. What are the wavelengths of the hydrogen spectrum, if they form first-order maxima at angles and when projected on a diffraction grating having 10,000 lines per centimeter?

Halfwave platenewport

The primary use for quarter wavelength retardation plates is to determine the optical sign of birefringence from interference figures observed in conoscopic mode with a Bertrand lens (Figures 3(c) and 3(d)). Insertion of a quarter wavelength retardation plate resolves the center of a uniaxial interference figure (Figure 3(c)) into two dark spots (Figure 3(d)). If the dark spots are positioned at right angles to the slow vibration axis of the compensator crystal (in quadrants two and four; Figure 3(d)), then the sign of birefringence for the crystal is positive. Conversely, if the dark spots are positioned parallel to the compensator crystal slow axis (in quadrants one and three; Figure 3(d)), the crystal has a negative sign of birefringence. Note that other rings in the interference pattern are translated either towards the center or the periphery of the pattern according to the optical sign. The interference pattern in Figure 3(c) was generated conoscopically using a polished thin section of the mineral lamproite, which exhibits negative birefringence. A similar technique can be employed to determine the optical sign of birefringence for biaxial crystals.

A diffraction grating has 2000 lines per centimeter. At what angle will the first-order maximum be for 520-nm-wavelength green light?

Diffraction gratings work both for transmission of light, as in (Figure), and for reflection of light, as on butterfly wings and the Australian opal in (Figure). Natural diffraction gratings also occur in the feathers of certain birds such as the hummingbird. Tiny, finger-like structures in regular patterns act as reflection gratings, producing constructive interference that gives the feathers colors not solely due to their pigmentation. This is called iridescence.

The extinction bands in polarized light images can be eliminated for image analysis purposes by inserting crossed quarter wavelength retardation plates into the microscope optical path with the specimen sandwiched between the two plates. In effect, the retardation introduced by the first quarter wavelength plate is precisely cancelled by the second, so that light reaching the analyzer contains only the retardation introduced by the specimen itself. In practice, one of the retardation plates is inserted into the nosepiece or intermediate tube slot with the slow vibration axis oriented Northeast-Southwest (by convention in modern microscopes). The second plate must be placed between the polarizer and the specimen (usually in or very near the condenser) with the slow axis oriented Northwest-Southeast. The two plates should be fabricated from the same material in order to completely eliminate extinction bands. If the two plates are accurately aligned, a minimum change of polarization colors will be observed in birefringent specimens as they are rotated through 360 degrees with the microscope circular stage. Images of purified riboflavin (Vitamin B2) crystallites in polarized light (Figure 3(e)) alone, and with quarter wavelength retardation plates inserted beneath the stage and above the objective rear aperture are illustrated in Figures 3(e) and 3(f), respectively. Note that the extinction regions of the spherulitic crystallite present in Figure 3(e) have been eliminated by the application of two quarter wavelength plates (Figure 3(f)), which more clearly defines the texture.

The analysis shown below also applies to diffraction gratings with lines separated by a distance d. What is the distance between fringes produced by a diffraction grating having 125 lines per centimeter for 600-nm light, if the screen is 1.50 m away? (Hint: The distance between adjacent fringes is assuming the slit separation d is comparable to )

Check Your Understanding If the line spacing of a diffraction grating d is not precisely known, we can use a light source with a well-determined wavelength to measure it. Suppose the first-order constructive fringe of the emission line of hydrogen is measured at using a spectrometer with a diffraction grating. What is the line spacing of this grating?

This concept is illustrated in Figures 3(a) and 3(b) for a polished thin section of tactic skarn, which contains inclusions that exhibit first and second order interference colors in polarized light without the presence of a retardation plate or compensator. When a first order retardation plate is employed to determine the optical sign of this birefringent ore, the interference colors are shifted up the Michel-Levy chart by a single wavelength and can lead to confusion during quantitative analysis. Conversely, using a quarter wavelength plate instead produces the customary first order yellow for the fast optical axis (Figure 3(a)) and second order blue hue for the slow axis (Figure 3(b)), allowing for easier identification of the optical properties.

a. , , , ; b. , , , ; c. Decreasing the number of lines per centimeter by a factor of x means that the angle for the x-order maximum is the same as the original angle for the first-order maximum.

Diffraction Gratings Copyright © by Samuel J. Ling; Jeff Sanny; and William Moebs is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Halfwave plate

(a) What do the four angles in the preceding problem become if a 5000-line per centimeter diffraction grating is used? (b) Using this grating, what would the angles be for the second-order maxima? (c) Discuss the relationship between integral reductions in lines per centimeter and the new angles of various order maxima.

Calculating Typical Diffraction Grating Effects Diffraction gratings with 10,000 lines per centimeter are readily available. Suppose you have one, and you send a beam of white light through it to a screen 2.00 m away. (a) Find the angles for the first-order diffraction of the shortest and longest wavelengths of visible light (380 and 760 nm, respectively). (b) What is the distance between the ends of the rainbow of visible light produced on the screen for first-order interference? (See (Figure).)

Quarter-WaveplateThorlabs

Calculate the wavelength of light that has its second-order maximum at when falling on a diffraction grating that has 5000 lines per centimeter.

In summary, the quarter wavelength retardation plate is capable of detecting optical path differences of (plus or minus) one-half wavelength by rotating the stage through 90 degrees. In this regard, the plate has a sensitivity range lying between the Bräce-Köhler and quartz wedge compensators and overlaps with the de Sénarmont compensator. Unlike many of the adjustable compensators, the quarter wavelength retardation plate can be effectively used in white light, but the most accurate results are obtained when the plate is coupled to the wavelength for which the crystal was prepared (for example, 548 nanometer green light for a 137 nanometer plate). The retardation plate can also be used to produce circularly polarized light by inserting it into the optical path above the polarizer.

Strategy Once a value for the diffraction grating’s slit spacing d has been determined, the angles for the sharp lines can be found using the equation

Quarter wave platepolarization

(a) Show that a 30,000 line per centimeter grating will not produce a maximum for visible light. (b) What is the longest wavelength for which it does produce a first-order maximum? (c) What is the greatest number of line per centimeter a diffraction grating can have and produce a complete second-order spectrum for visible light?

The quarter wavelength retardation plate is a common optical accessory for polarized light microscopy that operates by introducing a relative phase shift of 90 degrees between the orthogonal wavefronts (ordinary and extraordinary) passing through when the plate is illuminated with linearly polarized light. A phase shift of 90 degrees between the ordinary and extraordinary components converts the incident linear polarized light vibrations into either elliptical or circularly polarized light. Quarter wavelength retardation plates are useful for the qualitative analysis of conoscopic and orthoscopic images, and for the assessment of optical path differences in birefringent specimens.

An opal such as that shown in (Figure) acts like a reflection grating with rows separated by about If the opal is illuminated normally, (a) at what angle will red light be seen and (b) at what angle will blue light be seen?

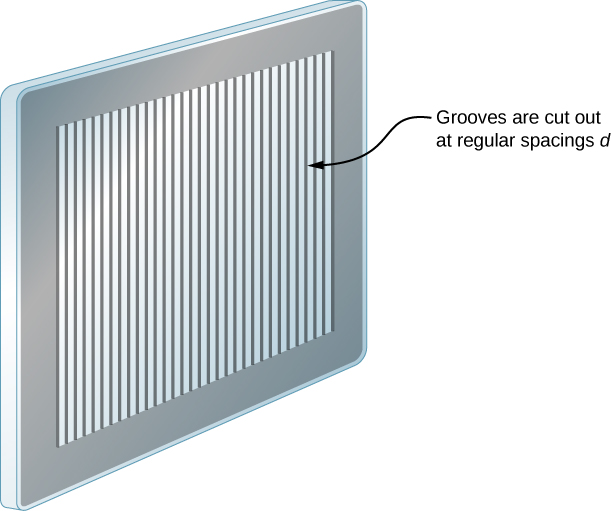
In reality, the number of slits is not infinite, but it can be very large—large enough to produce the equivalent effect. A prime example is an optical element called a diffraction grating. A diffraction grating can be manufactured by carving glass with a sharp tool in a large number of precisely positioned parallel lines, with untouched regions acting like slits ((Figure)). This type of grating can be photographically mass produced rather cheaply. Because there can be over 1000 lines per millimeter across the grating, when a section as small as a few millimeters is illuminated by an incoming ray, the number of illuminated slits is effectively infinite, providing for very sharp principal maxima.

Achromatic quarter-Waveplate

Find the angle for the third-order maximum for 580-nm-wavelength yellow light falling on a difraction grating having 1500 lines per centimeter.

Analyzing the interference of light passing through two slits lays out the theoretical framework of interference and gives us a historical insight into Thomas Young’s experiments. However, most modern-day applications of slit interference use not just two slits but many, approaching infinity for practical purposes. The key optical element is called a diffraction grating, an important tool in optical analysis.

Notice that in both equations, we reported the results of these intermediate calculations to four significant figures to use with the calculation in part (b).

How many lines per centimeter are there on a diffraction grating that gives a first-order maximum for 470-nm blue light at an angle of ?

(a) Find the maximum number of lines per centimeter a diffraction grating can have and produce a maximum for the smallest wavelength of visible light. (b) Would such a grating be useful for ultraviolet spectra? (c) For infrared spectra?