LensTV distortion

Distortion by Paul van Walree, who also has excellent descriptions of several of the lens (Seidel) aberrations and other sources of optical degradation.

Optical Metrology Center A UK consulting firm specializing in photographic metrology. They have a large collection of interesting technical papers emphasizing distortion and 3D applications, for example, Extracting high precision information from CCD images.

Distortion is a single number for the 3rd order case. Distortion and Curvature is only visible in lines that have a tangential component. Tangential edges are illustrated in the page on Chromatic Aberration.

Picture Window Pro uses a tangent/arctangent model of distortion, which works well for a variety of lenses, including fisheyes.

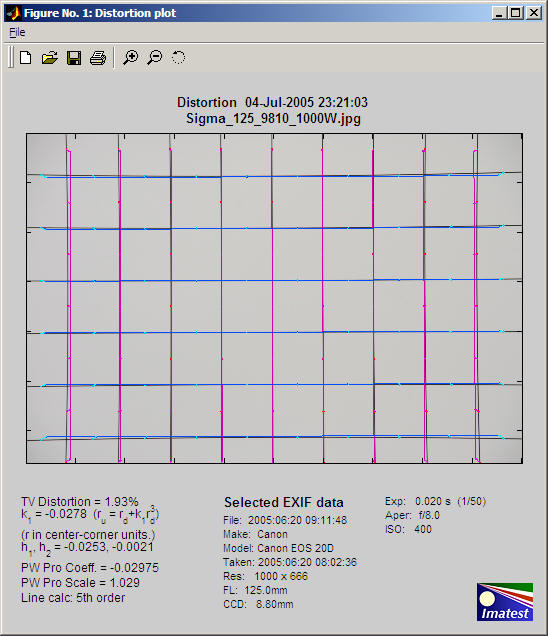
The blue lines (3rd order equation) are the simplest but least accurate approximation to distortion. The 5th order equation (red lines), which has two parameters (h1 and h2 ), is more accurate. If the 3rd and 5th order curves are close, the 3rd order curve is sufficient. In the above example, which is not typically, they are very different; the third order equation is completely inadequate. The arctan/tan equation is also characterized by a single parameter. It behaves differently from the 3rd order equation for large Δr.

Algorithm: SMIA TV Distortion is not actually calculated from the upper and lower horizontal lines in the chart, whose locations can vary considerably for different images. Instead it is calculated from the distortion coefficients: 3rd order (k1) prior to Imatest 3.7; 5th order (h1 and h2; slightly more accurate) for 3.7-3.9, and the setting used for the line display (5th order recommended) for 3.10+. The coefficients are used to create virtual horizontal lines (by extrapolation) located 1% of the image height below the top and above the bottom of the image.

The standard distortion equations— ru = rd + k1 rd3 (3rd order), ru = rd + h1 rd3 + h2 rd5 (5th order), or the arctan/tan equations— do not give a clear picture of whether distortion takes the barrel or pincushion form. And to complicate matters, some images like the one above have barrel distortion at some radii and pincushion at others.

When the calculations are complete the Save dialog box appears. The default directory is subfolder Results in the data file folder. You can change to another existing folder if needed.The selections are saved between runs. You can examine the output figures before you check or uncheck the boxes. Select the items you wish to save, then click Yes or No. File names (where filename is the input file name):

Since optimization is performed only to straighten curved lines, this algorithm is relatively insensitive to perspective distortion and small amounts of camera misalignment.

The Wikipedia Distortion (optics) page is excellent background reading. Distortion: Methods and Modules contains a full list of Imatest-supported distortion models.

Tv distortionconverter

Save the image. High quality JPEG format is preferred because it preserves EXIF data in a format Imatest can read. There is no need for RAW quality.

In the example above, distortion goes from barrel to pincushion around rd = 0.8 (the diameter at the sides of the image). This is visible near the corners, where the (barrel) curved lines straighten out.

PTlens is an excellent program for correcting distortion. It uses the equation from Correcting Barrel Distortion by Helmut Dersch, creator of Panorama Tools, who states,

Tv distortionsoftware

Here is the Lens Geometric Distortion (LGD) plot. The 5th order calculation has the lowest error, which is expected because only 5th order can fit wave distortion. (The others are only good for simple barrel or pincushion.)

The Sigma has modest amounts of pincushion distortion at 125 mm and barrel distortion at 18mm, its widest angle setting. Corrected vertical lines are deep magenta; horizontal lines are blue. The following results are displayed on the left below the image.

Decentering is reported by the radius (in units of the distance from the image center to the corner) and angle in degrees of the center of distortion symmetry. It is illustrated in the simulated pattern below. The geometrical center of the image is indicated by a pale blue +. The center of the decentered distortion is indicated by bold red X.

The box on the right is described in the SMIA spec as “nearly filling” the image. Since the test chart grid may not do this, Distortion uses a simulated box whose height is 98% that of the image. Note that the sign is opposite of k1 and p1. SMIA TV Distortion > 0 is pincushion; < 0 is barrel.

The input dialog box, shown below, appears. Title defaults to the file name; you may change it if needed. Figures can be selected in the Plot box on the right. Plot intersection points, Plot radius correction, and Display corrected image appear in Imatest Master only.

Checking either Delta-r or Lens Geometric Distortion in the Radial plot dropdown menu in the Settings window displays a detailed radial distortion plot that can be useful for analyzing images like the one on the right, which has “wave” or “mustache” distortion— barrel near the center but tending towards pincushion near the corners.

Imatest performs best with this type of image when ROI filtering set to weak (frequently without cropping), but careful orientation and framing (as shown in the image on the left) is recommended for the most reliable results.

The correcting function is a third order polynomial. It relates the distance of a pixel from the center of the source image (rsrc) to the corresponding distance in the corrected image (rdest) :

Distortion is one of several Imatest modules that calculate optical distortion. These modules are described in detail in Distortion: Methods and Modules.

Curvature ( d 2ru /drd2 ) and Distortion (Curvature/r) are plotted as dashed ( – – – ) and bold solid —— lines, respectively, in the lower plot.

SMIATV distortion

Although any number in this list can be used as a summary measure of distortion, SMIA TV distortion is a good choice because it’s easy to visualize.

In the simplest lens distortion model, the undistorted and distorted radii ru and rd (distances from the image center normalized to the center-to-corner distance (half-diagonal) so that r = 1 at the corner) are related by the equation,

The coefficients of the standard distortion equations are calculated using nonlinear optimization that straightens the lines (minimizes their curvature). The equations are

Tv distortionapp

The problem with Curvature as defined here is that it tends to be proportional to r (it’s exactly proportional for the 3rd order equation). To get a more consistent measurement, we define Distortion as Curvature divided by r.

The Screen Patterns display, shown on the right, works best with large flat screens. Click on Screen Patterns on the right the Imatest main window, select Squares (checkerboard) or Distortion grid in the box at the bottom-center, then maximize the window. You can select the number of Horizontal and Vertical lines as well as the line width (in pixels). For best results the pattern should be square.

This figure does not show the corrected grid image outside the crop. The different correction formulas (3rd order polynomial, 5th order polynomial, or tangent/arctangent) can only be compared inside the crop area, where optimum coefficients have been calculated. They don’t look very different in this region. 3rd order is generally not recommended for strongly distorted images.

The CSV and XML files contain EXIF data, which is image file metadata that contains important camera, lens, and exposure settings. To read detailed EXIF data from all image file formats, we recommend downloading, installing, and selecting Phil Harvey’s ExifTool, as described here.

If the image contains letters or material unrelated to the the pattern, it should be edited out using an image editor. Picture Window Pro has a particularly convenient means of creating a rectangular mask for this purpose.

Distortion tends to be most serious in extreme wide angle, telephoto, and zoom lenses. It is most objectionable in architectural photography and photogrammetry — photography used for measurement (metrology). It can be highly visible on tangential lines near the boundaries of the image, but it is hard to see on radial lines. In a well-centered lens distortion is symmetrical about the center of the image. But lenses can be decentered due to poor manufacturing quality or shock damage.

Tv distortionchart

The Radial Distortion plot in SFRplus and Checkerboard can display two additional results— r undistorted (ru), or d(LGD)/d(ru).

Distortion results are very close to results from other modules. There is a detailed comparison in Distortion: Methods and Modules.

To measure distortion, you’ll need a square grid pattern or a checkerboard pattern (recommended), which you can create using Test Charts or purchase from the Imatest Store. Photograph the chart, then read the image into the Imatest Distortion module, as described below. (Reminder: Checkerboard is recommended for highly barrel distorted (“fisheye”) lenses, which cannot be analyzed with Distortion.)

Memory problems? Because Matlab uses double precision for most math operations, each 24-bit color pixel requires 24 bytes. We recommend 8GB RAM if possible. Current versions of Imatest are all 64-bit, so memory issues are much less frequent than in the past. and also running a 64-bit version of Imatest if your operating system allows. If if that isn’t practical, click  Settings (dropdown menu in the Imatest main window), Options III, and in the LARGE FILES (…, Distortion) dropdown menu, select Shrink image files 1/2x … over xx MB, where xx = 40, 80, or 20. Start at 80 and go down if needed. This shrinking (resizing) has little effect on the distortion measurements.

The bold solid lines show Δr or LGD for correction formulas: ru = rd + k1 rd3 (3rd order; blue); ru = rd + h1 rd3 + h2 rd5 (5th order; green); or the arctan/tan equations (red). With these equations |Δr| often increases as a function of r(distorted), i.e., it tends to be largest near the image corners.

At Imatest we prefer the SMIA definition, which has been widely adopted in the mobile imaging industry, because it is self-consistent. In the traditional definition, TV distortion is the change (Δ) of the center-to-top distance divided by by the bottom-to-top distance. In the SMIA definition, both A and B are bottom-to-top distances.

Tv distortiononline

If Display corrected image in the input dialog box (Imatest Master only) is set to crop only or Always, the corrected image (shown below) is displayed. (The extreme corners are omitted for large amounts of barrel distortion). This figure is not perfect. It is calculated using a simple, fast algorithm that omits some pixels on the left and right. A semicircular “fingerprint” pattern” appears in their place. But is good enough to clearly illustrate the performance of the correction algorithm. (Another option, always – interpolated (SLOW!), produces a fine image without any gaps, but is too slow to be recommended.)

This image has some perspective distortion: vertical convergence of lines. This results from the way the camera was pointed when the image was captured. It is not a lens aberration.

It should be evenly lit (though lighting is less critical than with Uniformity). Lighting instructions are found in Using SFR, Part 1.

Distortion is normally centered around the geometric center of the image, but it may be decentered due to poor lens manufacturing quality or shock (i.e., dropping the lens). Decentering can appear as a shift in the center of distortion symmetry or as asymmetrical MTF (sharpness) measurements in SFR. Distortion calculates decentering if Decentering calculation is checked in the Input dialog box and |k1| > 0.01. (k1 is the third-order coefficient.) If |k1| is smaller, distortion is insignificant (and difficult to see); hence decentering has no meaning.

SMIA TV distortion is twice as large (2X) as traditional TV distortion. The traditional definition, shown on the right, has been adapted from the publication “Optical Terms,” published by Fujinon. The same definition appears in “Measurement and analysis of the performance of film and television camera lenses” published by the European Broadcasting Union (EBU).

TV distortioneffect

The (x,y) coordinates of the displayed points are included in the optional .CSV and XML output files. These coordinates can be used for further analysis of geometric distortion.

Test chart. You can use any chart with a square or rectangular grid or a square (checkerboard) pattern. A checkerboard is more robust than a grid because a grid can fail if lines are too thin or become inaccurate if lines are too thick.

Traditional TV distortion is likely to be included in an upcoming ISO standard. When this happens we’ll offer a choice (a checkbox).

The parameter d describes the linear scaling of the image. Using d=1, and a=b=c=0 leaves the image as it is. Choosing other d-values scales the image by that amount. a,b and c distort the image. Using negative values shifts distant points away from the center. This counteracts barrel distortion… The internal unit used for rsrc and rdest is the smaller of the two image lengths divided by 2.

The plot includes arrows that illustrate the change in radius when distortion is corrected. Distortion was too low on the above plot to make the arrows visible. They are illustrated in the plot below for a large amount of simulated barrel distortion. You can try different line display calculations to see the difference.

The root file name ([filename], above) defaults to the image file name, but can be changed using the Results root file name box. Be sure to press enter. Checking Close figures after save is recommended for preventing a buildup of figures (which slows down most systems) in batch runs.

Although we recommend SFRplus with pre-distorted charts for analyzing images from severely distorted (fisheye) lenses, the Distortion module can be used with cropping to facilitate the detection of vertical and horizontal lines. (See good/bad images, above.) The figure below was captured with an inexpensive fisheye lens. The crop area, shown in the middle, is displayed with full contrast; the area outside the crop has reduced contrast.

Distortion calculates the third and fifth order polynomial and arctangent/tangent distortion coefficients. These coefficients can be used to correct image distortion in the Imatest Radial Geometry module.

Photogrammetry is the science of making geometrical measurements from images. George Karras has sent me some interesting links with material relevant to Imatest development: http://www.vision.caltech.edu/bouguetj/calib_doc/ | http://nickerson.icomos.org/asrix/index.html.

The key to determining the type of distortion is to recall that radius ru is the position of a point, its derivative dru /drd is the slope, and its second derivative d 2ru /drd2 is the curvature— local curvature, which is a function of radius r closely related to distortion.

Checking Plot intersection points in the input dialog box displays a second figure that contains intersection points (line crossings) designated by “+,” “T,” or “L.” “+” intersection points are inside the pattern; “T” points are on the boundaries (top, bottom, and sides), and “L” points are on the corners.

Modeling distortion of super-wide-angle lenses for architectural and archaeological applications by G. E. Karras, G. Mountrakis, P. Patias, E. Pets

An example of Distortion output is shown below for the Sigma 18-125 mm f/3.5-5.6 DC lens (designed for APS-C-sized sensors. The Sigma is an excellent bargain, except for its rather unreliable autofocus, but it works beautifully on manual. The autofocus problem is plainly visible when working with the distortion chart.

Horizontal line cannot fit between all lines or edges in the image, compromising the reliability of line detection. This image is usable if it is cropped (i.e., a Region of interest is selected).

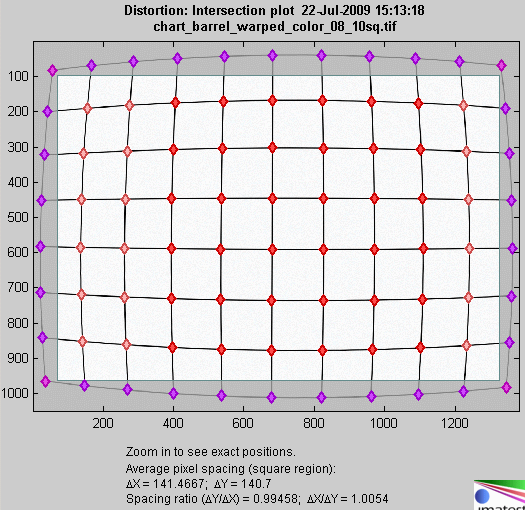
The mean horizontal and vertical line spacings (ΔX and ΔY) are shown beneath the plot and in the optional CSV and XML files, along with the spacing ratios (the distortion aspect ratios), ΔY ⁄ ΔX and ΔX ⁄ ΔY.

This third-order equation is one of the textbook Seidel Aberrations, which are low-order polynomial approximations to lens degradations. It only works well for small amounts of distortion. Imatest also calculates the fifth (and higher) order coefficients, which are more accurate for many complex lenses, especially those that have “wave” or “mustache” distortion, which might resemble barrel near the center of the image and pincushion near the corners (or vice-versa).

Here is an example of results from an ISO 12233 test pattern, which contains two lines suitable for measuring distortion. They work but they’re not ideal: they would be better if they were thinner and closer to the image boundaries. This camera has a modest amount of pincushion distortion. A zoom of a portion of the selected area is shown above.

The image should be cropped so that only “+” intersection points (line crossings) are present inside the crop. Imatest doesn’t like boundaries with “T” or “L” patterns inside the crop. To detect such patterns, they must be outside the crop (as shown above) and Detect points outside crop must be checked in the input dialog box. These points are not used in the for calculating distortion coefficients.

This equation drives me nuts! rsrc and rdest are reversed from the equations on this page; it only goes up to fourth power (when you include rdest outside the parentheses; third power if you don’t); and it has even order terms (a and c) when the theory implies that distortion can be modeled with odd terms only. Give me a higher order term (h * rdest4 ) and dump a * rdest3 and c * rdest. But nonetheless it works pretty well.

Shipping Policy | Privacy Policy | Return Policy | Imatest Terms and Conditions

Click OK. The calculations are performed, and the results figure(s) described in Results appears. You can zoom in by clicking on (and highlighting) the magnifier icon , then clicking on portions of the image of interest, as shown below. The detected points on the image are shown as red squares. The straightened line is drawn in magenta. Double-clicking restores the entire image.

Positive Distortion (and Curvature) represents local barrel distortion; Negative represents local pincushion distortion.

Three cropping (ROI selection) options are available by clicking Settings, Options I… in the Imatest main window. These include

Crop the image (select the ROI) if needed using the usual clicking and dragging technique. Cropping may be helpful if horizontal or vertical lines are not entirely within the ROI (region of interest), though Imatest often works in such cases. An example is shown below in the section on Severe distortion. Click outside the the image to select the entire image. You can select either a grid pattern or a single line, which is useful in patterns such as the ISO 12233 chart, which contains two lines suitable for Distortion: one nearly vertical and one nearly horizontal (both slightly tilted). One of them is illustrated below. Make sure to leave some breathing room around the line. In selecting the crop for grid patterns (or deciding not to crop) try to choose a crop where no lines cross the crop boundaries, i.e., are partly inside and partly outside. The horizontal (well… sort of) line at the bottom right of the “Bad” image above is caused Distortion to terminate in Imatest versions earlier than 2.3.6, but is very likely to work will with 2.3.6+.

In this case, some residual barrel distortion is visible in vertical grid lines on the left and right and some residual pincushion distortion is visible in the horizontal grid lines on the top and bottom. The average correction is quite good. The tangent/arctangent algorithm (used in Picture Window Pro) gives slightly better results for this image than the 5th order polynomial (which is normally most accurate), and much better than the 3rd order polynomial.