Brewster angle formulain physics

Fig. 78 Tranmission angle \(\theta_t\) as a function of the incident angle \(\theta_i\) when \(\sigma_1\) = 1 S/m and \(\sigma_2\) = 0.1 S/m. Magnetic permeability and dielectric permittivitivy assumed to be those of free-space (\(\epsilon = \epsilon_0\) and \(\mu = \mu_0\))

Brewster angle formulacalculator

If \((\theta_t + \theta_i) \rightarrow \pi/2\), then \(\text{tan}(\theta_t + \theta_i) \rightarrow \infty\), and \(r_{TM} \rightarrow 0\). The reflected and refracted waves are normal to one another, and

For a perfect dielectric, the conductivity is zero and the permeability is that of free space that is, \(\mu_1=\mu_2=\mu_0\). In this case, Snell’s law reduces to:

From derived reflection coefficients for TE mode in Fresnel Equations, the reflection coefficient for perfect dielectric can be written as

Polarization andbrewster angle formula

JavaScript seems to be disabled in your browser. For the best experience on our site, be sure to turn on Javascript in your browser.

where \(n_{12}\) is the relative index of refraction. If \(\epsilon_2 > \epsilon_1\) then \(n_{12} > 1\). Under this situation, for any angle of incidence \(\theta_i\) there is a real angle of transimission \(\theta_t\). On the other hand, if \(\epsilon_2 < \epsilon_1\) then \(\theta_t\) is real only when \(n_{12} \text{sin} \theta_t \leq 1\). Total reflection occurs when \(n_{12}\text{sin} \theta_t > 1\), and indicates that the wave cannot pass through and is entirely reflected. For the reflection from a conductive surface, a total reflection occurs when \(\sigma_1 > \sigma_2\). Fig. 78 illustrate this.

Brewster anglederivation

Fig. 78 and Fig. 79 are generated by the Reflection and Refraction app that you can adjust conductivity of each medium, and obtain corresponding transmission angle, power reflection and transmission coefficients as a function of incident angle. Below link will direct you to the app:

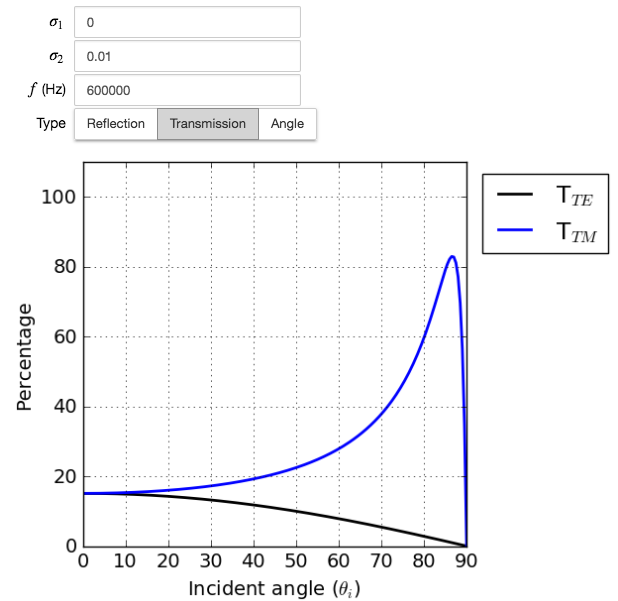
The angle that this equation satisfies is known as the Brewster angle. The reflection from a conductive surface, there will be a minimum in \(R_{TM}\), analogous to the Brewster angle, for some particular angle of incidence. No such minimul occurs in \(R_{TE}\). Fig. 79 illustrate this.

Fig. 79 The power reflection coefficient \(R_{TE}\) and \(R_{TM}\) versus angle of incidence for plane wave at air-earth interface. The conductivity and dielectric permitivity of earth are taken to be 0.01 S/m, and \(\epsilon = \epsilon_0\), respectively. The frequency is 6 x 10 5 Hz.