This is the distance from the center to a focus: c = a 2 − b 2 {\displaystyle c={\sqrt {a^{2}-b^{2}}}} .

where y int {\displaystyle y_{\text{int}}} , x int {\displaystyle x_{\text{int}}} are intercepts and x max {\displaystyle x_{\text{max}}} , y max {\displaystyle y_{\text{max}}} are maximum values. It follows directly from Apollonios's theorem.

Als Unternehmen können Sie von unseren attraktiven Paketen für Aussteller und Sponsoren profitieren. Werben Sie für sich und Ihr Angebot bei einer ausgewählten Zielgruppe technischer Fach- und Führungskräfte.

In analytic geometry, the ellipse is defined as a quadric: the set of points ( x , y ) {\displaystyle (x,\,y)} of the Cartesian plane that, in non-degenerate cases, satisfy the implicit equation[5][6] A x 2 + B x y + C y 2 + D x + E y + F = 0 {\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0} provided B 2 − 4 A C < 0. {\displaystyle B^{2}-4AC<0.}

For f → 0 = ( 0 0 ) , f → 1 = a ( cos ⁡ θ sin ⁡ θ ) , f → 2 = b ( − sin ⁡ θ cos ⁡ θ ) {\displaystyle {\vec {f}}_{0}={0 \choose 0},\;{\vec {f}}_{1}=a{\cos \theta \choose \sin \theta },\;{\vec {f}}_{2}=b{-\sin \theta \choose \;\cos \theta }} one obtains a parametric representation of the standard ellipse rotated by angle θ {\displaystyle \theta } : x = x θ ( t ) = a cos ⁡ θ cos ⁡ t − b sin ⁡ θ sin ⁡ t , y = y θ ( t ) = a sin ⁡ θ cos ⁡ t + b cos ⁡ θ sin ⁡ t . {\displaystyle {\begin{aligned}x&=x_{\theta }(t)=a\cos \theta \cos t-b\sin \theta \sin t\,,\\y&=y_{\theta }(t)=a\sin \theta \cos t+b\cos \theta \sin t\,.\end{aligned}}}

With help of trigonometric formulae one obtains: cos ⁡ t = cot ⁡ t ± 1 + cot 2 ⁡ t = − m a ± m 2 a 2 + b 2   , sin ⁡ t = 1 ± 1 + cot 2 ⁡ t = b ± m 2 a 2 + b 2 . {\displaystyle \cos t={\frac {\cot t}{\pm {\sqrt {1+\cot ^{2}t}}}}={\frac {-ma}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}\ ,\quad \quad \sin t={\frac {1}{\pm {\sqrt {1+\cot ^{2}t}}}}={\frac {b}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}.}

The exact infinite series is: C = 2 π a [ 1 − ( 1 2 ) 2 e 2 − ( 1 ⋅ 3 2 ⋅ 4 ) 2 e 4 3 − ( 1 ⋅ 3 ⋅ 5 2 ⋅ 4 ⋅ 6 ) 2 e 6 5 − ⋯ ] = 2 π a [ 1 − ∑ n = 1 ∞ ( ( 2 n − 1 ) ! ! ( 2 n ) ! ! ) 2 e 2 n 2 n − 1 ] = − 2 π a ∑ n = 0 ∞ ( ( 2 n − 1 ) ! ! ( 2 n ) ! ! ) 2 e 2 n 2 n − 1 , {\displaystyle {\begin{aligned}C&=2\pi a\left[{1-\left({\frac {1}{2}}\right)^{2}e^{2}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {e^{4}}{3}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}{\frac {e^{6}}{5}}-\cdots }\right]\\&=2\pi a\left[1-\sum _{n=1}^{\infty }\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}{\frac {e^{2n}}{2n-1}}\right]\\&=-2\pi a\sum _{n=0}^{\infty }\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}{\frac {e^{2n}}{2n-1}},\end{aligned}}} where n ! ! {\displaystyle n!!} is the double factorial (extended to negative odd integers in the usual way, giving ( − 1 ) ! ! = 1 {\displaystyle (-1)!!=1} and ( − 3 ) ! ! = − 1 {\displaystyle (-3)!!=-1} ).

For this family of ellipses, one introduces the following q-analog angle measure, which is not a function of the usual angle measure θ:[16][17]

Here m {\displaystyle m} is the slope of the tangent at the corresponding ellipse point, c → + {\displaystyle {\vec {c}}_{+}} is the upper and c → − {\displaystyle {\vec {c}}_{-}} the lower half of the ellipse. The vertices ( ± a , 0 ) {\displaystyle (\pm a,\,0)} , having vertical tangents, are not covered by the representation.

Using Dandelin spheres, one can prove that any section of a cone with a plane is an ellipse, assuming the plane does not contain the apex and has slope less than that of the lines on the cone.

This representation can be modeled technically by two simple methods. In both cases center, the axes and semi axes a , b {\displaystyle a,\,b} have to be known.

Using vectors, dot products and determinants this formula can be arranged more clearly, letting x → = ( x , y ) {\displaystyle {\vec {x}}=(x,\,y)} : ( x → − x → 1 ) ⋅ ( x → − x → 2 ) det ( x → − x → 1 , x → − x → 2 ) = ( x → 3 − x → 1 ) ⋅ ( x → 3 − x → 2 ) det ( x → 3 − x → 1 , x → 3 − x → 2 ) . {\displaystyle {\frac {\left({\color {red}{\vec {x}}}-{\vec {x}}_{1}\right)\cdot \left({\color {red}{\vec {x}}}-{\vec {x}}_{2}\right)}{\det \left({\color {red}{\vec {x}}}-{\vec {x}}_{1},{\color {red}{\vec {x}}}-{\vec {x}}_{2}\right)}}={\frac {\left({\vec {x}}_{3}-{\vec {x}}_{1}\right)\cdot \left({\vec {x}}_{3}-{\vec {x}}_{2}\right)}{\det \left({\vec {x}}_{3}-{\vec {x}}_{1},{\vec {x}}_{3}-{\vec {x}}_{2}\right)}}.}

where a {\displaystyle a} and b {\displaystyle b} are the lengths of the semi-major and semi-minor axes, respectively. The area formula π a b {\displaystyle \pi ab} is intuitive: start with a circle of radius b {\displaystyle b} (so its area is π b 2 {\displaystyle \pi b^{2}} ) and stretch it by a factor a / b {\displaystyle a/b} to make an ellipse. This scales the area by the same factor: π b 2 ( a / b ) = π a b . {\displaystyle \pi b^{2}(a/b)=\pi ab.} [18] However, using the same approach for the circumference would be fallacious – compare the integrals ∫ f ( x ) d x {\textstyle \int f(x)\,dx} and ∫ 1 + f ′ 2 ( x ) d x {\textstyle \int {\sqrt {1+f'^{2}(x)}}\,dx} . It is also easy to rigorously prove the area formula using integration as follows. Equation (1) can be rewritten as y ( x ) = b 1 − x 2 / a 2 . {\textstyle y(x)=b{\sqrt {1-x^{2}/a^{2}}}.} For x ∈ [ − a , a ] , {\displaystyle x\in [-a,a],} this curve is the top half of the ellipse. So twice the integral of y ( x ) {\displaystyle y(x)} over the interval [ − a , a ] {\displaystyle [-a,a]} will be the area of the ellipse: A ellipse = ∫ − a a 2 b 1 − x 2 a 2 d x = b a ∫ − a a 2 a 2 − x 2 d x . {\displaystyle {\begin{aligned}A_{\text{ellipse}}&=\int _{-a}^{a}2b{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\,dx\\&={\frac {b}{a}}\int _{-a}^{a}2{\sqrt {a^{2}-x^{2}}}\,dx.\end{aligned}}}

The width and height parameters a , b {\displaystyle a,\;b} are called the semi-major and semi-minor axes. The top and bottom points V 3 = ( 0 , b ) , V 4 = ( 0 , − b ) {\displaystyle V_{3}=(0,\,b),\;V_{4}=(0,\,-b)} are the co-vertices. The distances from a point ( x , y ) {\displaystyle (x,\,y)} on the ellipse to the left and right foci are a + e x {\displaystyle a+ex} and a − e x {\displaystyle a-ex} .

For the ellipse x 2 a 2 + y 2 b 2 = 1 {\displaystyle {\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1} the intersection points of orthogonal tangents lie on the circle x 2 + y 2 = a 2 + b 2 {\displaystyle x^{2}+y^{2}=a^{2}+b^{2}} .

Solving the parametric representation for cos ⁡ t , sin ⁡ t {\displaystyle \;\cos t,\sin t\;} by Cramer's rule and using cos 2 ⁡ t + sin 2 ⁡ t − 1 = 0 {\displaystyle \;\cos ^{2}t+\sin ^{2}t-1=0\;} , one obtains the implicit representation det ( x → − f → 0 , f → 2 ) 2 + det ( f → 1 , x → − f → 0 ) 2 − det ( f → 1 , f → 2 ) 2 = 0. {\displaystyle \det {\left({\vec {x}}\!-\!{\vec {f}}\!_{0},{\vec {f}}\!_{2}\right)^{2}}+\det {\left({\vec {f}}\!_{1},{\vec {x}}\!-\!{\vec {f}}\!_{0}\right)^{2}}-\det {\left({\vec {f}}\!_{1},{\vec {f}}\!_{2}\right)^{2}}=0.}

The standard form of an ellipse in Cartesian coordinates assumes that the origin is the center of the ellipse, the x-axis is the major axis, and:

An arbitrary line g {\displaystyle g} intersects an ellipse at 0, 1, or 2 points, respectively called an exterior line, tangent and secant. Through any point of an ellipse there is a unique tangent. The tangent at a point ( x 1 , y 1 ) {\displaystyle (x_{1},\,y_{1})} of the ellipse x 2 a 2 + y 2 b 2 = 1 {\displaystyle {\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1} has the coordinate equation: x 1 a 2 x + y 1 b 2 y = 1. {\displaystyle {\frac {x_{1}}{a^{2}}}x+{\frac {y_{1}}{b^{2}}}y=1.}

The two points c → 1 = p → ( t ) ,   c → 2 = p → ( t + π 2 ) {\textstyle {\vec {c}}_{1}={\vec {p}}(t),\ {\vec {c}}_{2}={\vec {p}}\left(t+{\frac {\pi }{2}}\right)} are on conjugate diameters (see previous section). From trigonometric formulae one obtains c → 2 = ( − a sin ⁡ t , b cos ⁡ t ) T {\displaystyle {\vec {c}}_{2}=(-a\sin t,\,b\cos t)^{\mathsf {T}}} and | c → 1 | 2 + | c → 2 | 2 = ⋯ = a 2 + b 2 . {\displaystyle \left|{\vec {c}}_{1}\right|^{2}+\left|{\vec {c}}_{2}\right|^{2}=\cdots =a^{2}+b^{2}\,.}

For example, for P 1 = ( 2 , 0 ) , P 2 = ( 0 , 1 ) , P 3 = ( 0 , 0 ) {\displaystyle P_{1}=(2,\,0),\;P_{2}=(0,\,1),\;P_{3}=(0,\,0)} the three-point equation is:

The definition of an ellipse in this section gives a parametric representation of an arbitrary ellipse, even in space, if one allows f → 0 , f → 1 , f → 2 {\displaystyle {\vec {f}}\!_{0},{\vec {f}}\!_{1},{\vec {f}}\!_{2}} to be vectors in space.

With the substitution u = tan ⁡ ( t 2 ) {\textstyle u=\tan \left({\frac {t}{2}}\right)} and trigonometric formulae one obtains cos ⁡ t = 1 − u 2 1 + u 2   , sin ⁡ t = 2 u 1 + u 2 {\displaystyle \cos t={\frac {1-u^{2}}{1+u^{2}}}\ ,\quad \sin t={\frac {2u}{1+u^{2}}}}

In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e {\displaystyle e} , a number ranging from e = 0 {\displaystyle e=0} (the limiting case of a circle) to e = 1 {\displaystyle e=1} (the limiting case of infinite elongation, no longer an ellipse but a parabola).

The characterization of an ellipse as the locus of points so that sum of the distances to the foci is constant leads to a method of drawing one using two drawing pins, a length of string, and a pencil. In this method, pins are pushed into the paper at two points, which become the ellipse's foci. A string is tied at each end to the two pins; its length after tying is 2 a {\displaystyle 2a} . The tip of the pencil then traces an ellipse if it is moved while keeping the string taut. Using two pegs and a rope, gardeners use this procedure to outline an elliptical flower bed—thus it is called the gardener's ellipse. The Byzantine architect Anthemius of Tralles (c. 600) described how this method could be used to construct an elliptical reflector,[13] and it was elaborated in a now-lost 9th-century treatise by Al-Ḥasan ibn Mūsā.[14]

With the abbreviations M = f → 1 2 + f → 2 2 ,   N = | det ( f → 1 , f → 2 ) | {\displaystyle \;M={\vec {f}}_{1}^{2}+{\vec {f}}_{2}^{2},\ N=\left|\det({\vec {f}}_{1},{\vec {f}}_{2})\right|} the statements of Apollonios's theorem can be written as: a 2 + b 2 = M , a b = N   . {\displaystyle a^{2}+b^{2}=M,\quad ab=N\ .} Solving this nonlinear system for a , b {\displaystyle a,b} yields the semiaxes: a = 1 2 ( M + 2 N + M − 2 N ) b = 1 2 ( M + 2 N − M − 2 N ) . {\displaystyle {\begin{aligned}a&={\frac {1}{2}}({\sqrt {M+2N}}+{\sqrt {M-2N}})\\[1ex]b&={\frac {1}{2}}({\sqrt {M+2N}}-{\sqrt {M-2N}})\,.\end{aligned}}}

Verwalten Sie Ihre Buchungen unkompliziert in Ihrem individuellen Kundenaccount. Hier finden Sie außerdem alle Veranstaltungsunterlagen zum Download.

A variation of the paper strip method 1 uses the observation that the midpoint N {\displaystyle N} of the paper strip is moving on the circle with center M {\displaystyle M} (of the ellipse) and radius a + b 2 {\displaystyle {\tfrac {a+b}{2}}} . Hence, the paperstrip can be cut at point N {\displaystyle N} into halves, connected again by a joint at N {\displaystyle N} and the sliding end K {\displaystyle K} fixed at the center M {\displaystyle M} (see diagram). After this operation the movement of the unchanged half of the paperstrip is unchanged.[15] This variation requires only one sliding shoe.

Some lower and upper bounds on the circumference of the canonical ellipse   x 2 / a 2 + y 2 / b 2 = 1   {\displaystyle \ x^{2}/a^{2}+y^{2}/b^{2}=1\ } with   a ≥ b   {\displaystyle \ a\geq b\ } are[25] 2 π b ≤ C ≤ 2 π a   , π ( a + b ) ≤ C ≤ 4 ( a + b )   , 4 a 2 + b 2   ≤ C ≤ 2   π a 2 + b 2     . {\displaystyle {\begin{aligned}2\pi b&\leq C\leq 2\pi a\ ,\\\pi (a+b)&\leq C\leq 4(a+b)\ ,\\4{\sqrt {a^{2}+b^{2}\ }}&\leq C\leq {\sqrt {2\ }}\pi {\sqrt {a^{2}+b^{2}\ }}~.\end{aligned}}}

For four points P i = ( x i , y i ) ,   i = 1 , 2 , 3 , 4 , {\displaystyle P_{i}=\left(x_{i},\,y_{i}\right),\ i=1,\,2,\,3,\,4,\,} no three of them on a line, we have the following (see diagram):

Keplerian elliptical orbits are the result of any radially directed attraction force whose strength is inversely proportional to the square of the distance. Thus, in principle, the motion of two oppositely charged particles in empty space would also be an ellipse. (However, this conclusion ignores losses due to electromagnetic radiation and quantum effects, which become significant when the particles are moving at high speed.)

More generally, in the gravitational two-body problem, if the two bodies are bound to each other (that is, the total energy is negative), their orbits are similar ellipses with the common barycenter being one of the foci of each ellipse. The other focus of either ellipse has no known physical significance. The orbit of either body in the reference frame of the other is also an ellipse, with the other body at the same focus.

Das VDI Wissensforum wächst! Du kannst ein Teil unserer Mission werden, Ingenieur*innen auf ihrem beruflichen Weg durch Wissen und Kompetenzen weiter zu bringen. Wir bieten dir hervorragende Arbeitsbedingungen – auch 2024 hat uns das Nachrichtenmagazin Focus als TOP Arbeitgeber Mittelstand ausgezeichnet.

If the water's surface is disturbed at one focus of an elliptical water tank, the circular waves of that disturbance, after reflecting off the walls, converge simultaneously to a single point: the second focus. This is a consequence of the total travel length being the same along any wall-bouncing path between the two foci.

For example, for P 1 = ( 2 , 0 ) , P 2 = ( 0 , 1 ) , P 3 = ( 0 , 0 ) {\displaystyle P_{1}=(2,\,0),\;P_{2}=(0,\,1),\;P_{3}=(0,\,0)} and q = 4 {\displaystyle q=4} one obtains the three-point form

An example gear application would be a device that winds thread onto a conical bobbin on a spinning machine. The bobbin would need to wind faster when the thread is near the apex than when it is near the base.[29]

Das VDI Wissensforum ist Ihr verlässlicher Partner rund um das Thema Weiterbildung für Ingenieure. Deshalb bieten wir Ihnen ein umfassendes Portfolio von gut 2.600 Tagungen, Konferenzen und Seminaren, die Sie auf Ihrem beruflichen Weg weiterbringen. Von A wie Automobil bis Z wie Zahnrad – bei uns finden Sie sicher das passende Thema und Ihr favorisiertes Format zur persönlichen Weiterbildung.

Alternately, if the parameter [ u : v ] {\displaystyle [u:v]} is considered to be a point on the real projective line P ( R ) {\textstyle \mathbf {P} (\mathbf {R} )} , then the corresponding rational parametrization is [ u : v ] ↦ ( a v 2 − u 2 v 2 + u 2 , b 2 u v v 2 + u 2 ) . {\displaystyle [u:v]\mapsto \left(a{\frac {v^{2}-u^{2}}{v^{2}+u^{2}}},b{\frac {2uv}{v^{2}+u^{2}}}\right).}

Replacing cos ⁡ t {\displaystyle \cos t} and sin ⁡ t {\displaystyle \sin t} of the standard representation yields: c → ± ( m ) = ( − m a 2 ± m 2 a 2 + b 2 , b 2 ± m 2 a 2 + b 2 ) , m ∈ R . {\displaystyle {\vec {c}}_{\pm }(m)=\left(-{\frac {ma^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}},\;{\frac {b^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}\right),\,m\in \mathbb {R} .}

Verwalten Sie Ihre Buchungen unkompliziert in Ihrem individuellen Kundenaccount. Hier finden Sie außerdem alle Veranstaltungsunterlagen zum Download.

Additionally, because of the focus-to-focus reflection property of ellipses, if the rays are allowed to continue propagating, reflected rays will eventually align closely with the major axis.

Analogously to the circle case, the equation can be written more clearly using vectors: ( x → − x → 1 ) ∗ ( x → − x → 2 ) det ( x → − x → 1 , x → − x → 2 ) = ( x → 3 − x → 1 ) ∗ ( x → 3 − x → 2 ) det ( x → 3 − x → 1 , x → 3 − x → 2 ) , {\displaystyle {\frac {\left({\color {red}{\vec {x}}}-{\vec {x}}_{1}\right)*\left({\color {red}{\vec {x}}}-{\vec {x}}_{2}\right)}{\det \left({\color {red}{\vec {x}}}-{\vec {x}}_{1},{\color {red}{\vec {x}}}-{\vec {x}}_{2}\right)}}={\frac {\left({\vec {x}}_{3}-{\vec {x}}_{1}\right)*\left({\vec {x}}_{3}-{\vec {x}}_{2}\right)}{\det \left({\vec {x}}_{3}-{\vec {x}}_{1},{\vec {x}}_{3}-{\vec {x}}_{2}\right)}},}

An affine transformation preserves parallelism and midpoints of line segments, so this property is true for any ellipse. (Note that the parallel chords and the diameter are no longer orthogonal.)

Ellipses are the closed type of conic section: a plane curve tracing the intersection of a cone with a plane (see figure). Ellipses have many similarities with the other two forms of conic sections, parabolas and hyperbolas, both of which are open and unbounded. An angled cross section of a right circular cylinder is also an ellipse.

Here f → 0 {\displaystyle {\vec {f}}\!_{0}} is the center and f → 1 , f → 2 {\displaystyle {\vec {f}}\!_{1},\;{\vec {f}}\!_{2}} are the directions of two conjugate diameters, in general not perpendicular.

Given an ellipse whose axes are drawn, we can construct the endpoints of a particular elliptic arc whose length is one eighth of the ellipse's circumference using only straightedge and compass in a finite number of steps; for some specific shapes of ellipses, such as when the axes have a length ratio of ⁠ 2 : 1 {\displaystyle {\sqrt {2}}:1} ⁠, it is additionally possible to construct the endpoints of a particular arc whose length is one twelfth of the circumference.[26] (The vertices and co-vertices are already endpoints of arcs whose length is one half or one quarter of the ellipse's circumference.) However, the general theory of straightedge-and-compass elliptic division appears to be unknown, unlike in the case of the circle and the lemniscate. The division in special cases has been investigated by Legendre in his classical treatise.[27]

Two non-circular gears with the same elliptical outline, each pivoting around one focus and positioned at the proper angle, turn smoothly while maintaining contact at all times. Alternatively, they can be connected by a link chain or timing belt, or in the case of a bicycle the main chainring may be elliptical, or an ovoid similar to an ellipse in form. Such elliptical gears may be used in mechanical equipment to produce variable angular speed or torque from a constant rotation of the driving axle, or in the case of a bicycle to allow a varying crank rotation speed with inversely varying mechanical advantage.

The circumference of the ellipse may be evaluated in terms of E ( e ) {\displaystyle E(e)} using Gauss's arithmetic-geometric mean;[19] this is a quadratically converging iterative method (see here for details).

In principle, the canonical ellipse equation x 2 a 2 + y 2 b 2 = 1 {\displaystyle {\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1} may have a < b {\displaystyle a

For an arbitrary point ( x , y ) {\displaystyle (x,y)} the distance to the focus ( c , 0 ) {\displaystyle (c,0)} is ( x − c ) 2 + y 2 {\textstyle {\sqrt {(x-c)^{2}+y^{2}}}} and to the other focus ( x + c ) 2 + y 2 {\textstyle {\sqrt {(x+c)^{2}+y^{2}}}} . Hence the point ( x , y ) {\displaystyle (x,\,y)} is on the ellipse whenever: ( x − c ) 2 + y 2 + ( x + c ) 2 + y 2 = 2 a   . {\displaystyle {\sqrt {(x-c)^{2}+y^{2}}}+{\sqrt {(x+c)^{2}+y^{2}}}=2a\ .}

a , b = − 2 ( A E 2 + C D 2 − B D E + ( B 2 − 4 A C ) F ) ( ( A + C ) ± ( A − C ) 2 + B 2 ) B 2 − 4 A C , x ∘ = 2 C D − B E B 2 − 4 A C , y ∘ = 2 A E − B D B 2 − 4 A C , θ = 1 2 atan2 ⁡ ( − B , C − A ) , {\displaystyle {\begin{aligned}a,b&={\frac {-{\sqrt {2{\big (}AE^{2}+CD^{2}-BDE+(B^{2}-4AC)F{\big )}{\big (}(A+C)\pm {\sqrt {(A-C)^{2}+B^{2}}}{\big )}}}}{B^{2}-4AC}},\\x_{\circ }&={\frac {2CD-BE}{B^{2}-4AC}},\\[5mu]y_{\circ }&={\frac {2AE-BD}{B^{2}-4AC}},\\[5mu]\theta &={\tfrac {1}{2}}\operatorname {atan2} (-B,\,C-A),\end{aligned}}}

Such a relation between points and lines generated by a conic is called pole-polar relation or polarity. The pole is the point; the polar the line.

In polar coordinates, with the origin at the center of the ellipse and with the angular coordinate θ {\displaystyle \theta } measured from the major axis, the ellipse's equation is[7]: 75  r ( θ ) = a b ( b cos ⁡ θ ) 2 + ( a sin ⁡ θ ) 2 = b 1 − ( e cos ⁡ θ ) 2 {\displaystyle r(\theta )={\frac {ab}{\sqrt {(b\cos \theta )^{2}+(a\sin \theta )^{2}}}}={\frac {b}{\sqrt {1-(e\cos \theta )^{2}}}}} where e {\displaystyle e} is the eccentricity, not Euler's number.

In the 17th century, Johannes Kepler discovered that the orbits along which the planets travel around the Sun are ellipses with the Sun [approximately] at one focus, in his first law of planetary motion. Later, Isaac Newton explained this as a corollary of his law of universal gravitation.

Here the upper bound   2 π a   {\displaystyle \ 2\pi a\ } is the circumference of a circumscribed concentric circle passing through the endpoints of the ellipse's major axis, and the lower bound 4 a 2 + b 2 {\displaystyle 4{\sqrt {a^{2}+b^{2}}}} is the perimeter of an inscribed rhombus with vertices at the endpoints of the major and the minor axes.

The case F 1 = F 2 {\displaystyle F_{1}=F_{2}} yields a circle and is included as a special type of ellipse.

The general equation's coefficients can be obtained from known semi-major axis a {\displaystyle a} , semi-minor axis b {\displaystyle b} , center coordinates ( x ∘ , y ∘ ) {\displaystyle \left(x_{\circ },\,y_{\circ }\right)} , and rotation angle θ {\displaystyle \theta } (the angle from the positive horizontal axis to the ellipse's major axis) using the formulae: A = a 2 sin 2 ⁡ θ + b 2 cos 2 ⁡ θ B = 2 ( b 2 − a 2 ) sin ⁡ θ cos ⁡ θ C = a 2 cos 2 ⁡ θ + b 2 sin 2 ⁡ θ D = − 2 A x ∘ − B y ∘ E = − B x ∘ − 2 C y ∘ F = A x ∘ 2 + B x ∘ y ∘ + C y ∘ 2 − a 2 b 2 . {\displaystyle {\begin{aligned}A&=a^{2}\sin ^{2}\theta +b^{2}\cos ^{2}\theta &B&=2\left(b^{2}-a^{2}\right)\sin \theta \cos \theta \\[1ex]C&=a^{2}\cos ^{2}\theta +b^{2}\sin ^{2}\theta &D&=-2Ax_{\circ }-By_{\circ }\\[1ex]E&=-Bx_{\circ }-2Cy_{\circ }&F&=Ax_{\circ }^{2}+Bx_{\circ }y_{\circ }+Cy_{\circ }^{2}-a^{2}b^{2}.\end{aligned}}}

An ellipse defined implicitly by A x 2 + B x y + C y 2 = 1 {\displaystyle Ax^{2}+Bxy+Cy^{2}=1} has area 2 π / 4 A C − B 2 . {\displaystyle 2\pi /{\sqrt {4AC-B^{2}}}.}

The substitution p = f ( 1 + e ) {\displaystyle p=f(1+e)} yields x 2 ( e 2 − 1 ) + 2 p x − y 2 = 0. {\displaystyle x^{2}\left(e^{2}-1\right)+2px-y^{2}=0.}

This is the equation of an ellipse ( e < 1 {\displaystyle e<1} ), or a parabola ( e = 1 {\displaystyle e=1} ), or a hyperbola ( e > 1 {\displaystyle e>1} ). All of these non-degenerate conics have, in common, the origin as a vertex (see diagram).

If instead we use polar coordinates with the origin at one focus, with the angular coordinate θ = 0 {\displaystyle \theta =0} still measured from the major axis, the ellipse's equation is r ( θ ) = a ( 1 − e 2 ) 1 ± e cos ⁡ θ {\displaystyle r(\theta )={\frac {a(1-e^{2})}{1\pm e\cos \theta }}}

The diagram shows an easy way to find the centers of curvature C 1 = ( a − b 2 a , 0 ) , C 3 = ( 0 , b − a 2 b ) {\displaystyle C_{1}=\left(a-{\tfrac {b^{2}}{a}},0\right),\,C_{3}=\left(0,b-{\tfrac {a^{2}}{b}}\right)} at vertex V 1 {\displaystyle V_{1}} and co-vertex V 3 {\displaystyle V_{3}} , respectively:

Radius of curvature at the two vertices ( ± a , 0 ) {\displaystyle (\pm a,0)} and the centers of curvature: ρ 0 = b 2 a = p   , ( ± c 2 a | 0 )   . {\displaystyle \rho _{0}={\frac {b^{2}}{a}}=p\ ,\qquad \left(\pm {\frac {c^{2}}{a}}\,{\bigg |}\,0\right)\ .}

any pair of points p → ( t ) ,   p → ( t + π ) {\displaystyle {\vec {p}}(t),\ {\vec {p}}(t+\pi )} belong to a diameter, and the pair p → ( t + π 2 ) ,   p → ( t − π 2 ) {\displaystyle {\vec {p}}\left(t+{\tfrac {\pi }{2}}\right),\ {\vec {p}}\left(t-{\tfrac {\pi }{2}}\right)} belong to its conjugate diameter.

Studienbereich Optotechnik und Bildverarbeitung (OBV), Fachbereich Mathematik und Naturwissenschaften, Hochschule Darmstadt

The center of the circle ( x ∘ , y ∘ ) {\displaystyle \left(x_{\circ },\,y_{\circ }\right)} satisfies: [ 1 y 1 − y 2 x 1 − x 2 x 1 − x 3 y 1 − y 3 1 ] [ x ∘ y ∘ ] = [ x 1 2 − x 2 2 + y 1 2 − y 2 2 2 ( x 1 − x 2 ) y 1 2 − y 3 2 + x 1 2 − x 3 2 2 ( y 1 − y 3 ) ] . {\displaystyle {\begin{bmatrix}1&{\dfrac {y_{1}-y_{2}}{x_{1}-x_{2}}}\\[2ex]{\dfrac {x_{1}-x_{3}}{y_{1}-y_{3}}}&1\end{bmatrix}}{\begin{bmatrix}x_{\circ }\\[1ex]y_{\circ }\end{bmatrix}}={\begin{bmatrix}{\dfrac {x_{1}^{2}-x_{2}^{2}+y_{1}^{2}-y_{2}^{2}}{2(x_{1}-x_{2})}}\\[2ex]{\dfrac {y_{1}^{2}-y_{3}^{2}+x_{1}^{2}-x_{3}^{2}}{2(y_{1}-y_{3})}}\end{bmatrix}}.}

where q is fixed and x ∘ , y ∘ , a {\displaystyle x_{\circ },\,y_{\circ },\,a} vary over the real numbers. (Such ellipses have their axes parallel to the coordinate axes: if q < 1 {\displaystyle q<1} , the major axis is parallel to the x-axis; if q > 1 {\displaystyle q>1} , it is parallel to the y-axis.)

which covers any point of the ellipse x 2 a 2 + y 2 b 2 = 1 {\displaystyle {\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1} except the left vertex ( − a , 0 ) {\displaystyle (-a,\,0)} .

An ellipse may also be defined in terms of one focal point and a line outside the ellipse called the directrix: for all points on the ellipse, the ratio between the distance to the focus and the distance to the directrix is a constant. This constant ratio is the above-mentioned eccentricity: e = c a = 1 − b 2 a 2 . {\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}.}

BildverarbeitungEnglisch

where E ( z ∣ m ) {\displaystyle E(z\mid m)} is the incomplete elliptic integral of the second kind with parameter m = k 2 . {\displaystyle m=k^{2}.}

Similarly, if a light source is placed at one focus of an elliptic mirror, all light rays on the plane of the ellipse are reflected to the second focus. Since no other smooth curve has such a property, it can be used as an alternative definition of an ellipse. (In the special case of a circle with a source at its center all light would be reflected back to the center.) If the ellipse is rotated along its major axis to produce an ellipsoidal mirror (specifically, a prolate spheroid), this property holds for all rays out of the source. Alternatively, a cylindrical mirror with elliptical cross-section can be used to focus light from a linear fluorescent lamp along a line of the paper; such mirrors are used in some document scanners.

The area can also be expressed in terms of eccentricity and the length of the semi-major axis as a 2 π 1 − e 2 {\displaystyle a^{2}\pi {\sqrt {1-e^{2}}}} (obtained by solving for flattening, then computing the semi-minor axis).

Bildverarbeitungsoftware

From Apollonios theorem (see below) one obtains: The area of an ellipse x → = f → 0 + f → 1 cos ⁡ t + f → 2 sin ⁡ t {\displaystyle \;{\vec {x}}={\vec {f}}_{0}+{\vec {f}}_{1}\cos t+{\vec {f}}_{2}\sin t\;} is A = π | det ( f → 1 , f → 2 ) | . {\displaystyle A=\pi \left|\det({\vec {f}}_{1},{\vec {f}}_{2})\right|.}

The proof for the pair F 1 , l 1 {\displaystyle F_{1},l_{1}} follows from the fact that | P F 1 | 2 = ( x − c ) 2 + y 2 ,   | P l 1 | 2 = ( x − a 2 c ) 2 {\textstyle \left|PF_{1}\right|^{2}=(x-c)^{2}+y^{2},\ \left|Pl_{1}\right|^{2}=\left(x-{\tfrac {a^{2}}{c}}\right)^{2}} and y 2 = b 2 − b 2 a 2 x 2 {\displaystyle y^{2}=b^{2}-{\tfrac {b^{2}}{a^{2}}}x^{2}} satisfy the equation | P F 1 | 2 − c 2 a 2 | P l 1 | 2 = 0 . {\displaystyle \left|PF_{1}\right|^{2}-{\frac {c^{2}}{a^{2}}}\left|Pl_{1}\right|^{2}=0\,.}

Because the tangent line is perpendicular to the normal, an equivalent statement is that the tangent is the external angle bisector of the lines to the foci (see diagram). Let L {\displaystyle L} be the point on the line P F 2 ¯ {\displaystyle {\overline {PF_{2}}}} with distance 2 a {\displaystyle 2a} to the focus F 2 {\displaystyle F_{2}} , where a {\displaystyle a} is the semi-major axis of the ellipse. Let line w {\displaystyle w} be the external angle bisector of the lines P F 1 ¯ {\displaystyle {\overline {PF_{1}}}} and P F 2 ¯ . {\displaystyle {\overline {PF_{2}}}.} Take any other point Q {\displaystyle Q} on w . {\displaystyle w.} By the triangle inequality and the angle bisector theorem, 2 a = | L F 2 | < {\displaystyle 2a=\left|LF_{2}\right|<{}} | Q F 2 | + | Q L | = {\displaystyle \left|QF_{2}\right|+\left|QL\right|={}} | Q F 2 | + | Q F 1 | , {\displaystyle \left|QF_{2}\right|+\left|QF_{1}\right|,} therefore Q {\displaystyle Q} must be outside the ellipse. As this is true for every choice of Q , {\displaystyle Q,} w {\displaystyle w} only intersects the ellipse at the single point P {\displaystyle P} so must be the tangent line.

Das Seminar macht Sie vertraut mit der Rolle der Sensorik bei der digitalen Transformation. Werden Sie zum Sensorexperten im Bereich Internet of Things.

The parameter t (called the eccentric anomaly in astronomy) is not the angle of ( x ( t ) , y ( t ) ) {\displaystyle (x(t),y(t))} with the x-axis, but has a geometric meaning due to Philippe de La Hire (see § Drawing ellipses below).[8]

So far we have dealt with erect ellipses, whose major and minor axes are parallel to the x {\displaystyle x} and y {\displaystyle y} axes. However, some applications require tilted ellipses. In charged-particle beam optics, for instance, the enclosed area of an erect or tilted ellipse is an important property of the beam, its emittance. In this case a simple formula still applies, namely

To distinguish the degenerate cases from the non-degenerate case, let ∆ be the determinant Δ = | A 1 2 B 1 2 D 1 2 B C 1 2 E 1 2 D 1 2 E F | = A C F + 1 4 B D E − 1 4 ( A E 2 + C D 2 + F B 2 ) . {\displaystyle \Delta ={\begin{vmatrix}A&{\frac {1}{2}}B&{\frac {1}{2}}D\\{\frac {1}{2}}B&C&{\frac {1}{2}}E\\{\frac {1}{2}}D&{\frac {1}{2}}E&F\end{vmatrix}}=ACF+{\tfrac {1}{4}}BDE-{\tfrac {1}{4}}(AE^{2}+CD^{2}+FB^{2}).}

Because of c ⋅ a 2 c = a 2 {\displaystyle c\cdot {\tfrac {a^{2}}{c}}=a^{2}} point L 1 {\displaystyle L_{1}} of directrix l 1 {\displaystyle l_{1}} (see diagram) and focus F 1 {\displaystyle F_{1}} are inverse with respect to the circle inversion at circle x 2 + y 2 = a 2 {\displaystyle x^{2}+y^{2}=a^{2}} (in diagram green). Hence L 1 {\displaystyle L_{1}} can be constructed as shown in the diagram. Directrix l 1 {\displaystyle l_{1}} is the perpendicular to the main axis at point L 1 {\displaystyle L_{1}} .

This section considers the family of ellipses defined by equations ( x − x ∘ ) 2 a 2 + ( y − y ∘ ) 2 b 2 = 1 {\displaystyle {\tfrac {\left(x-x_{\circ }\right)^{2}}{a^{2}}}+{\tfrac {\left(y-y_{\circ }\right)^{2}}{b^{2}}}=1} with a fixed eccentricity e {\displaystyle e} . It is convenient to use the parameter: q = a 2 b 2 = 1 1 − e 2 , {\displaystyle {\color {blue}q}={\frac {a^{2}}{b^{2}}}={\frac {1}{1-e^{2}}},}

The ellipse is a special case of the hypotrochoid when R = 2 r {\displaystyle R=2r} , as shown in the adjacent image. The special case of a moving circle with radius r {\displaystyle r} inside a circle with radius R = 2 r {\displaystyle R=2r} is called a Tusi couple.

For any method described below, knowledge of the axes and the semi-axes is necessary (or equivalently: the foci and the semi-major axis). If this presumption is not fulfilled one has to know at least two conjugate diameters. With help of Rytz's construction the axes and semi-axes can be retrieved.

The general solution for a harmonic oscillator in two or more dimensions is also an ellipse. Such is the case, for instance, of a long pendulum that is free to move in two dimensions; of a mass attached to a fixed point by a perfectly elastic spring; or of any object that moves under influence of an attractive force that is directly proportional to its distance from a fixed attractor. Unlike Keplerian orbits, however, these "harmonic orbits" have the center of attraction at the geometric center of the ellipse, and have fairly simple equations of motion.

P {\displaystyle P} is the center of the rectangle V 1 , V 2 , B , A {\displaystyle V_{1},\,V_{2},\,B,\,A} . The side A B ¯ {\displaystyle {\overline {AB}}} of the rectangle is divided into n equal spaced line segments and this division is projected parallel with the diagonal A V 2 {\displaystyle AV_{2}} as direction onto the line segment V 1 B ¯ {\displaystyle {\overline {V_{1}B}}} and assign the division as shown in the diagram. The parallel projection together with the reverse of the orientation is part of the projective mapping between the pencils at V 1 {\displaystyle V_{1}} and V 2 {\displaystyle V_{2}} needed. The intersection points of any two related lines V 1 B i {\displaystyle V_{1}B_{i}} and V 2 A i {\displaystyle V_{2}A_{i}} are points of the uniquely defined ellipse. With help of the points C 1 , … {\displaystyle C_{1},\,\dotsc } the points of the second quarter of the ellipse can be determined. Analogously one obtains the points of the lower half of the ellipse.

This series converges, but by expanding in terms of h = ( a − b ) 2 / ( a + b ) 2 , {\displaystyle h=(a-b)^{2}/(a+b)^{2},} James Ivory,[20] Bessel[21] and Kummer[22] derived an expression that converges much more rapidly. It is most concisely written in terms of the binomial coefficient with n = 1 / 2 {\displaystyle n=1/2} : C π ( a + b ) = ∑ n = 0 ∞ ( 1 2 n ) 2 h n = ∑ n = 0 ∞ ( ( 2 n − 3 ) ! ! ( 2 n ) ! ! ) 2 h n = ∑ n = 0 ∞ ( ( 2 n − 3 ) ! ! 2 n n ! ) 2 h n = 1 + h 4 + h 2 64 + h 3 256 + 25 h 4 16384 + 49 h 5 65536 + 441 h 6 2 20 + 1089 h 7 2 22 + ⋯ . {\displaystyle {\begin{aligned}{\frac {C}{\pi (a+b)}}&=\sum _{n=0}^{\infty }{{\frac {1}{2}} \choose n}^{2}h^{n}\\&=\sum _{n=0}^{\infty }\left({\frac {(2n-3)!!}{(2n)!!}}\right)^{2}h^{n}\\&=\sum _{n=0}^{\infty }\left({\frac {(2n-3)!!}{2^{n}n!}}\right)^{2}h^{n}\\&=1+{\frac {h}{4}}+{\frac {h^{2}}{64}}+{\frac {h^{3}}{256}}+{\frac {25\,h^{4}}{16384}}+{\frac {49\,h^{5}}{65536}}+{\frac {441\,h^{6}}{2^{20}}}+{\frac {1089\,h^{7}}{2^{22}}}+\cdots .\end{aligned}}} The coefficients are slightly smaller (by a factor of 2 n − 1 {\displaystyle 2n-1} ), but also h {\displaystyle h} is numerically much smaller than e {\displaystyle e} except at h = e = 0 {\displaystyle h=e=0} and h = e = 1 {\displaystyle h=e=1} . For eccentricities less than 0.5 ( h < 0.005 {\displaystyle h<0.005} ), the error is at the limits of double-precision floating-point after the h 4 {\displaystyle h^{4}} term.[23]

The area of the triangle generated by c → 1 , c → 2 {\displaystyle {\vec {c}}_{1},\,{\vec {c}}_{2}} is A Δ = 1 2 det ( c → 1 , c → 2 ) = ⋯ = 1 2 a b {\displaystyle A_{\Delta }={\tfrac {1}{2}}\det \left({\vec {c}}_{1},\,{\vec {c}}_{2}\right)=\cdots ={\tfrac {1}{2}}ab}

Then the arc length s {\displaystyle s} from   x 1   {\displaystyle \ x_{1}\ } to   x 2   {\displaystyle \ x_{2}\ } is: s = − b ∫ arccos ⁡ x 1 a arccos ⁡ x 2 a   1 + ( a 2 b 2 − 1 )   sin 2 ⁡ z   d z   . {\displaystyle s=-b\int _{\arccos {\frac {x_{1}}{a}}}^{\arccos {\frac {x_{2}}{a}}}{\sqrt {\ 1+\left({\tfrac {a^{2}}{b^{2}}}-1\right)\ \sin ^{2}z~}}\;dz~.}

Der Karrierebereich bietet dir Eindrücke von den verschiedenen Teams und Bereichen. Außerdem kannst du dich über unsere aktuellen Stellenangebote informieren. Du hast noch Fragen zu deiner Bewerbung? Dann kontaktiere uns!

and to write the ellipse equation as: ( x − x ∘ ) 2 + q ( y − y ∘ ) 2 = a 2 , {\displaystyle \left(x-x_{\circ }\right)^{2}+{\color {blue}q}\,\left(y-y_{\circ }\right)^{2}=a^{2},}

Digitalebildverarbeitung

At first the measure is available only for chords not parallel to the y-axis, but the final formula works for any chord.

The two following methods rely on the parametric representation (see § Standard parametric representation, above): ( a cos ⁡ t , b sin ⁡ t ) {\displaystyle (a\cos t,\,b\sin t)}

The length of the chord through one focus, perpendicular to the major axis, is called the latus rectum. One half of it is the semi-latus rectum ℓ {\displaystyle \ell } . A calculation shows:[4] ℓ = b 2 a = a ( 1 − e 2 ) . {\displaystyle \ell ={\frac {b^{2}}{a}}=a\left(1-e^{2}\right).}

The four vertices of the ellipse are p → ( t 0 ) , p → ( t 0 ± π 2 ) , p → ( t 0 + π ) {\displaystyle {\vec {p}}(t_{0}),\;{\vec {p}}\left(t_{0}\pm {\tfrac {\pi }{2}}\right),\;{\vec {p}}\left(t_{0}+\pi \right)} , for a parameter t = t 0 {\displaystyle t=t_{0}} defined by: cot ⁡ ( 2 t 0 ) = f → 1 2 − f → 2 2 2 f → 1 ⋅ f → 2 . {\displaystyle \cot(2t_{0})={\frac {{\vec {f}}\!_{1}^{\,2}-{\vec {f}}\!_{2}^{\,2}}{2{\vec {f}}\!_{1}\cdot {\vec {f}}\!_{2}}}.}

One marks the point, which divides the strip into two substrips of length b {\displaystyle b} and a − b {\displaystyle a-b} . The strip is positioned onto the axes as described in the diagram. Then the free end of the strip traces an ellipse, while the strip is moved. For the proof, one recognizes that the tracing point can be described parametrically by ( a cos ⁡ t , b sin ⁡ t ) {\displaystyle (a\cos t,\,b\sin t)} , where parameter t {\displaystyle t} is the angle of slope of the paper strip.

c 2 {\displaystyle c_{2}} is called the circular directrix (related to focus F 2 {\displaystyle F_{2}} ) of the ellipse.[1][2] This property should not be confused with the definition of an ellipse using a directrix line below.

and from the diagram it can be seen that the area of the parallelogram is 8 times that of A Δ {\displaystyle A_{\Delta }} . Hence Area 12 = 4 a b . {\displaystyle {\text{Area}}_{12}=4ab\,.}

The eccentricity can be expressed as: e = c a = 1 − ( b a ) 2 , {\displaystyle e={\frac {c}{a}}={\sqrt {1-\left({\frac {b}{a}}\right)^{2}}},}

It is sometimes useful to find the minimum bounding ellipse on a set of points. The ellipsoid method is quite useful for solving this problem.

At a vertex parameter t = t 0 {\displaystyle t=t_{0}} , the tangent is perpendicular to the major/minor axes, so: 0 = p → ′ ( t ) ⋅ ( p → ( t ) − f → 0 ) = ( − f → 1 sin ⁡ t + f → 2 cos ⁡ t ) ⋅ ( f → 1 cos ⁡ t + f → 2 sin ⁡ t ) . {\displaystyle 0={\vec {p}}'(t)\cdot \left({\vec {p}}(t)-{\vec {f}}\!_{0}\right)=\left(-{\vec {f}}\!_{1}\sin t+{\vec {f}}\!_{2}\cos t\right)\cdot \left({\vec {f}}\!_{1}\cos t+{\vec {f}}\!_{2}\sin t\right).}

The angle θ {\displaystyle \theta } is called the true anomaly of the point. The numerator ℓ = a ( 1 − e 2 ) {\displaystyle \ell =a(1-e^{2})} is the semi-latus rectum.

Using (1) one finds that ( − y 1 a 2 x 1 b 2 ) {\displaystyle {\begin{pmatrix}-y_{1}a^{2}&x_{1}b^{2}\end{pmatrix}}} is a tangent vector at point ( x 1 , y 1 ) {\displaystyle (x_{1},\,y_{1})} , which proves the vector equation.

Ellipses appear in descriptive geometry as images (parallel or central projection) of circles. There exist various tools to draw an ellipse. Computers provide the fastest and most accurate method for drawing an ellipse. However, technical tools (ellipsographs) to draw an ellipse without a computer exist. The principle was known to the 5th century mathematician Proclus, and the tool now known as an elliptical trammel was invented by Leonardo da Vinci.[11]

BildverarbeitungKI

In the parametric equation for a general ellipse given above, x → = p → ( t ) = f → 0 + f → 1 cos ⁡ t + f → 2 sin ⁡ t , {\displaystyle {\vec {x}}={\vec {p}}(t)={\vec {f}}\!_{0}+{\vec {f}}\!_{1}\cos t+{\vec {f}}\!_{2}\sin t,}

The following construction of single points of an ellipse is due to de La Hire.[12] It is based on the standard parametric representation ( a cos ⁡ t , b sin ⁡ t ) {\displaystyle (a\cos t,\,b\sin t)} of an ellipse:

More generally, the arc length of a portion of the circumference, as a function of the angle subtended (or x coordinates of any two points on the upper half of the ellipse), is given by an incomplete elliptic integral. The upper half of an ellipse is parameterized by y = b   1 − x 2 a 2     . {\displaystyle y=b\ {\sqrt {1-{\frac {x^{2}}{a^{2}}}\ }}~.}

It is beneficial to use a parametric formulation in computer graphics because the density of points is greatest where there is the most curvature. Thus, the change in slope between each successive point is small, reducing the apparent "jaggedness" of the approximation.

If the focus is F = ( f 1 , f 2 ) {\displaystyle F=\left(f_{1},\,f_{2}\right)} and the directrix u x + v y + w = 0 {\displaystyle ux+vy+w=0} , one obtains the equation ( x − f 1 ) 2 + ( y − f 2 ) 2 = e 2 ( u x + v y + w ) 2 u 2 + v 2   . {\displaystyle \left(x-f_{1}\right)^{2}+\left(y-f_{2}\right)^{2}=e^{2}{\frac {\left(ux+vy+w\right)^{2}}{u^{2}+v^{2}}}\ .}

For u ∈ [ 0 , 1 ] , {\displaystyle u\in [0,\,1],} this formula represents the right upper quarter of the ellipse moving counter-clockwise with increasing u . {\displaystyle u.} The left vertex is the limit lim u → ± ∞ ( x ( u ) , y ( u ) ) = ( − a , 0 ) . {\textstyle \lim _{u\to \pm \infty }(x(u),\,y(u))=(-a,\,0)\;.}

Two diameters d 1 , d 2 {\displaystyle d_{1},\,d_{2}} of an ellipse are conjugate if the midpoints of chords parallel to d 1 {\displaystyle d_{1}} lie on d 2   . {\displaystyle d_{2}\ .}

Als Referent bietet sich Ihnen die Gelegenheit, ein spezifisches Publikum anzusprechen und sich oder Ihr Unternehmen effizient zu platzieren. So können Sie mit Ihrem Fachwissen zu spannenden Diskussionen beitragen und diese mitgestalten.

(If f → 1 ⋅ f → 2 = 0 {\displaystyle {\vec {f}}\!_{1}\cdot {\vec {f}}\!_{2}=0} , then t 0 = 0 {\displaystyle t_{0}=0} .) This is derived as follows. The tangent vector at point p → ( t ) {\displaystyle {\vec {p}}(t)} is: p → ′ ( t ) = − f → 1 sin ⁡ t + f → 2 cos ⁡ t   . {\displaystyle {\vec {p}}\,'(t)=-{\vec {f}}\!_{1}\sin t+{\vec {f}}\!_{2}\cos t\ .}

assuming a > b . {\displaystyle a>b.} An ellipse with equal axes ( a = b {\displaystyle a=b} ) has zero eccentricity, and is a circle.

Removing the radicals by suitable squarings and using b 2 = a 2 − c 2 {\displaystyle b^{2}=a^{2}-c^{2}} (see diagram) produces the standard equation of the ellipse:[3] x 2 a 2 + y 2 b 2 = 1 , {\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,} or, solved for y: y = ± b a a 2 − x 2 = ± ( a 2 − x 2 ) ( 1 − e 2 ) . {\displaystyle y=\pm {\frac {b}{a}}{\sqrt {a^{2}-x^{2}}}=\pm {\sqrt {\left(a^{2}-x^{2}\right)\left(1-e^{2}\right)}}.}

This circle is called orthoptic or director circle of the ellipse (not to be confused with the circular directrix defined above).

For elliptical orbits, useful relations involving the eccentricity e {\displaystyle e} are: e = r a − r p r a + r p = r a − r p 2 a r a = ( 1 + e ) a r p = ( 1 − e ) a {\displaystyle {\begin{aligned}e&={\frac {r_{a}-r_{p}}{r_{a}+r_{p}}}={\frac {r_{a}-r_{p}}{2a}}\\r_{a}&=(1+e)a\\r_{p}&=(1-e)a\end{aligned}}}

The equation of the tangent at point c → ± ( m ) {\displaystyle {\vec {c}}_{\pm }(m)} has the form y = m x + n {\displaystyle y=mx+n} . The still unknown n {\displaystyle n} can be determined by inserting the coordinates of the corresponding ellipse point c → ± ( m ) {\displaystyle {\vec {c}}_{\pm }(m)} : y = m x ± m 2 a 2 + b 2 . {\displaystyle y=mx\pm {\sqrt {m^{2}a^{2}+b^{2}}}\,.}

IndustrielleBildverarbeitung

Steiner generation can also be defined for hyperbolas and parabolas. It is sometimes called a parallelogram method because one can use other points rather than the vertices, which starts with a parallelogram instead of a rectangle.

(The choice e = 1 {\displaystyle e=1} yields a parabola, and if e > 1 {\displaystyle e>1} , a hyperbola.)

An affine transformation of the Euclidean plane has the form x → ↦ f → 0 + A x → {\displaystyle {\vec {x}}\mapsto {\vec {f}}\!_{0}+A{\vec {x}}} , where A {\displaystyle A} is a regular matrix (with non-zero determinant) and f → 0 {\displaystyle {\vec {f}}\!_{0}} is an arbitrary vector. If f → 1 , f → 2 {\displaystyle {\vec {f}}\!_{1},{\vec {f}}\!_{2}} are the column vectors of the matrix A {\displaystyle A} , the unit circle ( cos ⁡ ( t ) , sin ⁡ ( t ) ) {\displaystyle (\cos(t),\sin(t))} , 0 ≤ t ≤ 2 π {\displaystyle 0\leq t\leq 2\pi } , is mapped onto the ellipse: x → = p → ( t ) = f → 0 + f → 1 cos ⁡ t + f → 2 sin ⁡ t . {\displaystyle {\vec {x}}={\vec {p}}(t)={\vec {f}}\!_{0}+{\vec {f}}\!_{1}\cos t+{\vec {f}}\!_{2}\sin t\,.}

of an ellipse centered at the origin is given, then the two vectors f → 1 = ( e 0 ) , f → 2 = e d 2 − c 2 ( − c 1 ) {\displaystyle {\vec {f}}_{1}={e \choose 0},\quad {\vec {f}}_{2}={\frac {e}{\sqrt {d^{2}-c^{2}}}}{-c \choose 1}} point to two conjugate points and the tools developed above are applicable.

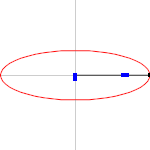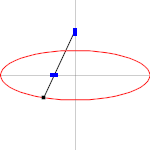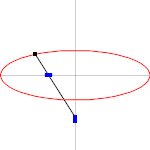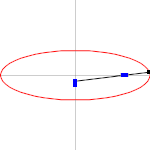
The midpoint C {\displaystyle C} of the line segment joining the foci is called the center of the ellipse. The line through the foci is called the major axis, and the line perpendicular to it through the center is the minor axis. The major axis intersects the ellipse at two vertices V 1 , V 2 {\displaystyle V_{1},V_{2}} , which have distance a {\displaystyle a} to the center. The distance c {\displaystyle c} of the foci to the center is called the focal distance or linear eccentricity. The quotient e = c a {\displaystyle e={\tfrac {c}{a}}} is the eccentricity.

Each of the two lines parallel to the minor axis, and at a distance of d = a 2 c = a e {\textstyle d={\frac {a^{2}}{c}}={\frac {a}{e}}} from it, is called a directrix of the ellipse (see diagram).

Any ellipse can be described in a suitable coordinate system by an equation x 2 a 2 + y 2 b 2 = 1 {\displaystyle {\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1} . The equation of the tangent at a point P 1 = ( x 1 , y 1 ) {\displaystyle P_{1}=\left(x_{1},\,y_{1}\right)} of the ellipse is x 1 x a 2 + y 1 y b 2 = 1. {\displaystyle {\tfrac {x_{1}x}{a^{2}}}+{\tfrac {y_{1}y}{b^{2}}}=1.} If one allows point P 1 = ( x 1 , y 1 ) {\displaystyle P_{1}=\left(x_{1},\,y_{1}\right)} to be an arbitrary point different from the origin, then

The point, where the semi axes meet is marked by P {\displaystyle P} . If the strip slides with both ends on the axes of the desired ellipse, then point P {\displaystyle P} traces the ellipse. For the proof one shows that point P {\displaystyle P} has the parametric representation ( a cos ⁡ t , b sin ⁡ t ) {\displaystyle (a\cos t,\,b\sin t)} , where parameter t {\displaystyle t} is the angle of the slope of the paper strip.

The second integral is the area of a circle of radius a , {\displaystyle a,} that is, π a 2 . {\displaystyle \pi a^{2}.} So A ellipse = b a π a 2 = π a b . {\displaystyle A_{\text{ellipse}}={\frac {b}{a}}\pi a^{2}=\pi ab.}

In case of a circle the last equation collapses to x 1 x 2 + y 1 y 2 = 0   . {\displaystyle x_{1}x_{2}+y_{1}y_{2}=0\ .}

An ellipse has a simple algebraic solution for its area, but for its perimeter (also known as circumference), integration is required to obtain an exact solution.

The circumference C {\displaystyle C} of an ellipse is: C = 4 a ∫ 0 π / 2 1 − e 2 sin 2 ⁡ θ   d θ = 4 a E ( e ) {\displaystyle C\,=\,4a\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta \,=\,4a\,E(e)}

For the generation of points of the ellipse x 2 a 2 + y 2 b 2 = 1 {\displaystyle {\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1} one uses the pencils at the vertices V 1 , V 2 {\displaystyle V_{1},\,V_{2}} . Let P = ( 0 , b ) {\displaystyle P=(0,\,b)} be an upper co-vertex of the ellipse and A = ( − a , 2 b ) , B = ( a , 2 b ) {\displaystyle A=(-a,\,2b),\,B=(a,\,2b)} .

The equation | P F 2 | + | P F 1 | = 2 a {\displaystyle \left|PF_{2}\right|+\left|PF_{1}\right|=2a} can be viewed in a different way (see figure):

(The right side of the equation uses the Hesse normal form of a line to calculate the distance | P l | {\displaystyle |Pl|} .)

This is equivalent to s = b   [ E ( z | 1 − a 2 b 2 ) ] z   =   arccos ⁡ x 2 a arccos ⁡ x 1 a {\displaystyle s=b\ \left[\;E\left(z\;{\Biggl |}\;1-{\frac {a^{2}}{b^{2}}}\right)\;\right]_{z\ =\ \arccos {\frac {x_{2}}{a}}}^{\arccos {\frac {x_{1}}{a}}}}

It follows from the equation that the ellipse is symmetric with respect to the coordinate axes and hence with respect to the origin.

Composite Bézier curves may also be used to draw an ellipse to sufficient accuracy, since any ellipse may be construed as an affine transformation of a circle. The spline methods used to draw a circle may be used to draw an ellipse, since the constituent Bézier curves behave appropriately under such transformations.

At first the measure is available only for chords which are not parallel to the y-axis. But the final formula works for any chord. The proof follows from a straightforward calculation. For the direction of proof given that the points are on an ellipse, one can assume that the center of the ellipse is the origin.

In statistics, a bivariate random vector ( X , Y ) {\displaystyle (X,Y)} is jointly elliptically distributed if its iso-density contours—loci of equal values of the density function—are ellipses. The concept extends to an arbitrary number of elements of the random vector, in which case in general the iso-density contours are ellipsoids. A special case is the multivariate normal distribution. The elliptical distributions are important in finance because if rates of return on assets are jointly elliptically distributed then all portfolios can be characterized completely by their mean and variance—that is, any two portfolios with identical mean and variance of portfolio return have identical distributions of portfolio return.[32][33]

Das VDI Wissensforum verbindet seit über 60 Jahren Tradition und Innovation. Erfahre mehr über unsere Werte und unsere Geschichte im Portrait-Bereich. Für Neuigkeiten vom Wissensforum oder aus der Welt der Ingenieur*innen stehen dir spannende News zur Verfügung.

The radius is the distance between any of the three points and the center. r = ( x 1 − x ∘ ) 2 + ( y 1 − y ∘ ) 2 = ( x 2 − x ∘ ) 2 + ( y 2 − y ∘ ) 2 = ( x 3 − x ∘ ) 2 + ( y 3 − y ∘ ) 2 . {\displaystyle r={\sqrt {\left(x_{1}-x_{\circ }\right)^{2}+\left(y_{1}-y_{\circ }\right)^{2}}}={\sqrt {\left(x_{2}-x_{\circ }\right)^{2}+\left(y_{2}-y_{\circ }\right)^{2}}}={\sqrt {\left(x_{3}-x_{\circ }\right)^{2}+\left(y_{3}-y_{\circ }\right)^{2}}}.}

Sound waves are reflected in a similar way, so in a large elliptical room a person standing at one focus can hear a person standing at the other focus remarkably well. The effect is even more evident under a vaulted roof shaped as a section of a prolate spheroid. Such a room is called a whisper chamber. The same effect can be demonstrated with two reflectors shaped like the end caps of such a spheroid, placed facing each other at the proper distance. Examples are the National Statuary Hall at the United States Capitol (where John Quincy Adams is said to have used this property for eavesdropping on political matters); the Mormon Tabernacle at Temple Square in Salt Lake City, Utah; at an exhibit on sound at the Museum of Science and Industry in Chicago; in front of the University of Illinois at Urbana–Champaign Foellinger Auditorium; and also at a side chamber of the Palace of Charles V, in the Alhambra.

Expanding and applying the identities cos 2 ⁡ t − sin 2 ⁡ t = cos ⁡ 2 t ,     2 sin ⁡ t cos ⁡ t = sin ⁡ 2 t {\displaystyle \;\cos ^{2}t-\sin ^{2}t=\cos 2t,\ \ 2\sin t\cos t=\sin 2t\;} gives the equation for t = t 0 . {\displaystyle t=t_{0}\;.}

A technical realization of the motion of the paper strip can be achieved by a Tusi couple (see animation). The device is able to draw any ellipse with a fixed sum a + b {\displaystyle a+b} , which is the radius of the large circle. This restriction may be a disadvantage in real life. More flexible is the second paper strip method.

Srinivasa Ramanujan gave two close approximations for the circumference in §16 of "Modular Equations and Approximations to π {\displaystyle \pi } ";[24] they are C ≈ π [ 3 ( a + b ) − ( 3 a + b ) ( a + 3 b ) ] = π [ 3 ( a + b ) − 3 ( a + b ) 2 + 4 a b ] {\displaystyle C\approx \pi {\biggl [}3(a+b)-{\sqrt {(3a+b)(a+3b)}}{\biggr ]}=\pi {\biggl [}3(a+b)-{\sqrt {3(a+b)^{2}+4ab}}{\biggr ]}} and C ≈ π ( a + b ) ( 1 + 3 h 10 + 4 − 3 h ) , {\displaystyle C\approx \pi \left(a+b\right)\left(1+{\frac {3h}{10+{\sqrt {4-3h}}}}\right),} where h {\displaystyle h} takes on the same meaning as above. The errors in these approximations, which were obtained empirically, are of order h 3 {\displaystyle h^{3}} and h 5 , {\displaystyle h^{5},} respectively.

Im Seminar "Grundlagen der Robot-Vision" lernen Sie, wie ein solches System aufgebaut ist und wie Sie das geeignete System für Ihre Aufgabe finden.

which is the equation of an ellipse with center ( a , 0 ) {\displaystyle (a,\,0)} , the x-axis as major axis, and the major/minor semi axis a , b {\displaystyle a,\,b} .

Analytically, the equation of a standard ellipse centered at the origin with width 2 a {\displaystyle 2a} and height 2 b {\displaystyle 2b} is: x 2 a 2 + y 2 b 2 = 1. {\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.}

Example: For the ellipse with equation x 2 + 2 x y + 3 y 2 − 1 = 0 {\displaystyle \;x^{2}+2xy+3y^{2}-1=0\;} the vectors are f → 1 = ( 1 0 ) , f → 2 = 1 2 ( − 1 1 ) . {\displaystyle {\vec {f}}_{1}={1 \choose 0},\quad {\vec {f}}_{2}={\frac {1}{\sqrt {2}}}{-1 \choose 1}.}

If e < 1 {\displaystyle e<1} , introduce new parameters a , b {\displaystyle a,\,b} so that 1 − e 2 = b 2 a 2 ,  and    p = b 2 a {\displaystyle 1-e^{2}={\tfrac {b^{2}}{a^{2}}},{\text{ and }}\ p={\tfrac {b^{2}}{a}}} , and then the equation above becomes ( x − a ) 2 a 2 + y 2 b 2 = 1 , {\displaystyle {\frac {(x-a)^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1\,,}

where the sign in the denominator is negative if the reference direction θ = 0 {\displaystyle \theta =0} points towards the center (as illustrated on the right), and positive if that direction points away from the center.

Industrialbildverarbeitung

In 1970 Danny Cohen presented at the "Computer Graphics 1970" conference in England a linear algorithm for drawing ellipses and circles. In 1971, L. B. Smith published similar algorithms for all conic sections and proved them to have good properties.[36] These algorithms need only a few multiplications and additions to calculate each vector.

where ∗ {\displaystyle *} is the modified dot product u → ∗ v → = u x v x + q u y v y . {\displaystyle {\vec {u}}*{\vec {v}}=u_{x}v_{x}+{\color {blue}q}\,u_{y}v_{y}.}

Throughout this article, the semi-major and semi-minor axes are denoted a {\displaystyle a} and b {\displaystyle b} , respectively, i.e. a ≥ b > 0   . {\displaystyle a\geq b>0\ .}

A circle with equation ( x − x ∘ ) 2 + ( y − y ∘ ) 2 = r 2 {\displaystyle \left(x-x_{\circ }\right)^{2}+\left(y-y_{\circ }\right)^{2}=r^{2}} is uniquely determined by three points ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) {\displaystyle \left(x_{1},y_{1}\right),\;\left(x_{2},\,y_{2}\right),\;\left(x_{3},\,y_{3}\right)} not on a line. A simple way to determine the parameters x ∘ , y ∘ , r {\displaystyle x_{\circ },y_{\circ },r} uses the inscribed angle theorem for circles:

The semi-latus rectum ℓ {\displaystyle \ell } is equal to the radius of curvature at the vertices (see section curvature).

BildverarbeitungJobs

Ellipses are common in physics, astronomy and engineering. For example, the orbit of each planet in the Solar System is approximately an ellipse with the Sun at one focus point (more precisely, the focus is the barycenter of the Sun–planet pair). The same is true for moons orbiting planets and all other systems of two astronomical bodies. The shapes of planets and stars are often well described by ellipsoids. A circle viewed from a side angle looks like an ellipse: that is, the ellipse is the image of a circle under parallel or perspective projection. The ellipse is also the simplest Lissajous figure formed when the horizontal and vertical motions are sinusoids with the same frequency: a similar effect leads to elliptical polarization of light in optics.

For the common parametric representation ( a cos ⁡ t , b sin ⁡ t ) {\displaystyle (a\cos t,b\sin t)} of the ellipse with equation x 2 a 2 + y 2 b 2 = 1 {\displaystyle {\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1} one gets: The points

A vector parametric equation of the tangent is: x → = ( x 1 y 1 ) + s ( − y 1 a 2 x 1 b 2 ) , s ∈ R . {\displaystyle {\vec {x}}={\begin{pmatrix}x_{1}\\y_{1}\end{pmatrix}}+s\left({\begin{array}{r}-y_{1}a^{2}\\x_{1}b^{2}\end{array}}\right),\quad s\in \mathbb {R} .}

The extension to e = 0 {\displaystyle e=0} , which is the eccentricity of a circle, is not allowed in this context in the Euclidean plane. However, one may consider the directrix of a circle to be the line at infinity in the projective plane.

Bildverarbeitungssoftware

Drawing an ellipse as a graphics primitive is common in standard display libraries, such as the MacIntosh QuickDraw API, and Direct2D on Windows. Jack Bresenham at IBM is most famous for the invention of 2D drawing primitives, including line and circle drawing, using only fast integer operations such as addition and branch on carry bit. M. L. V. Pitteway extended Bresenham's algorithm for lines to conics in 1967.[34] Another efficient generalization to draw ellipses was invented in 1984 by Jerry Van Aken.[35]

Similar to the variation of the paper strip method 1 a variation of the paper strip method 2 can be established (see diagram) by cutting the part between the axes into halves.

Assuming a ≥ b {\displaystyle a\geq b} , the foci are ( ± c , 0 ) {\displaystyle (\pm c,0)} for c = a 2 − b 2 {\textstyle c={\sqrt {a^{2}-b^{2}}}} . The standard parametric equation is: ( x , y ) = ( a cos ⁡ ( t ) , b sin ⁡ ( t ) ) for 0 ≤ t ≤ 2 π . {\displaystyle (x,y)=(a\cos(t),b\sin(t))\quad {\text{for}}\quad 0\leq t\leq 2\pi .}

If ( x 1 , y 1 ) {\displaystyle (x_{1},y_{1})} and ( u , v ) {\displaystyle (u,v)} are two points of the ellipse such that x 1 u a 2 + y 1 v b 2 = 0 {\textstyle {\frac {x_{1}u}{a^{2}}}+{\tfrac {y_{1}v}{b^{2}}}=0} , then the points lie on two conjugate diameters (see below). (If a = b {\displaystyle a=b} , the ellipse is a circle and "conjugate" means "orthogonal".)

This description of the tangents of an ellipse is an essential tool for the determination of the orthoptic of an ellipse. The orthoptic article contains another proof, without differential calculus and trigonometric formulae.