In laser systems, Gaussian beams are essential for describing the spatial distribution of the laser light within the resonator cavity. Understanding the properties of Gaussian beams is critical for optimizing the performance of lasers, including maximizing output power, minimizing beam divergence, and achieving a stable and well-defined beam profile.

Gaussian beamwaist

Gaussian beamwaist calculator

Pancake lenses consist of two to four lenses. As a first optimization to enable high imaging quality, all lens surfaces have an aspherical profile. A new feature is that defined multiple reflections are used in the lens and the optical surfaces are thus used several times. This makes a more compact design possible. Polarization-selective and polarization-rotating coatings are used on the lens surface to intensify the light intensity in the desired beam path.

Gaussian beamradius

Gaussian beamcalculator

A promising alternative approach is the use of pancake lenses. Although these are a bit thicker than Fresnel lenses, they can be positioned much closer to the display with a distance of less than 1 mm. Thus, they reduce the size of the VR lens system. At the same time, they improve the optical quality by eliminating the edge structure as they are less sensitive to stray light.

Gaussian beampdf

Gaussian beams can be transformed using optical elements to achieve specific beam profiles and focal characteristics. Beam shaping techniques, such as using diffractive optical elements or spatial light modulators, can modify the intensity distribution of the beam to meet specific application requirements. Additionally, Gaussian beams’ unique focusing properties make them indispensable in applications such as laser cutting, material processing, and medical procedures.

Did this article inspire you? Are you looking for further knowledge transfer? Then you might also be interested in the following topics …

Due to their complexity, pancake lenses present manufacturers with many difficulties. Errors are caused by unwanted reflection or transmission on the wrong surface. These become visible as haze, which reduces the contrast of the image as a whole, or ghost images, local image superimpositions of a part of the image. Thus, precise geometric positioning of all components is very critical. In detail, the following must be observed:

A Gaussian beam is described by its beam waist, which represents the point of minimum beam diameter, and its divergence angle, which determines how the beam expands as it propagates. The intensity profile of a Gaussian beam follows a bell-shaped curve, with the highest intensity at the beam center and decreasing towards the edges. These characteristics make Gaussian beams particularly well-suited for many optical applications. Figure 1 is presented as the 3DOptics calculator of the Gaussian beam. Each beam parameter can be estimated during the definition of other parameters.

The first headset models used Fresnel lenses. These have one advantage: They themselves are already very thin and light. Unfortunately, the required distance of more than 50 mm between the optics and the display is quite large. Furthermore, Fresnel lenses are very sensitive to stray light due to their edge structure.

One of the fundamental concepts that play a crucial role in optical engineering is that of Gaussian beams. Gaussian beams are special laser beams characterized by their unique intensity distribution and propagation characteristics. Their importance in optical engineering and simulation of optical designs cannot be overstated, as they are a powerful tool in understanding and predicting the behavior of light in various optical systems.

Gaussian beamintensity formula

Gaussian beam laserpdf

TRIOPTICS’ expertise in active alignment and optical metrology enables our customers to design and manufacture better pancake lenses for tomorrow’s challenges. During the manufacturing process and quality inspection, the following parameters are adjusted or controlled:

In the simulation of optical designs, Gaussian beam modeling serves as a valuable starting point. Optical design software often employs Gaussian beam approximations to provide initial estimations of the optical system’s performance. These simulations enable engineers to explore different design parameters efficiently and rapidly iterate on potential solutions, saving time and resources in the design process.

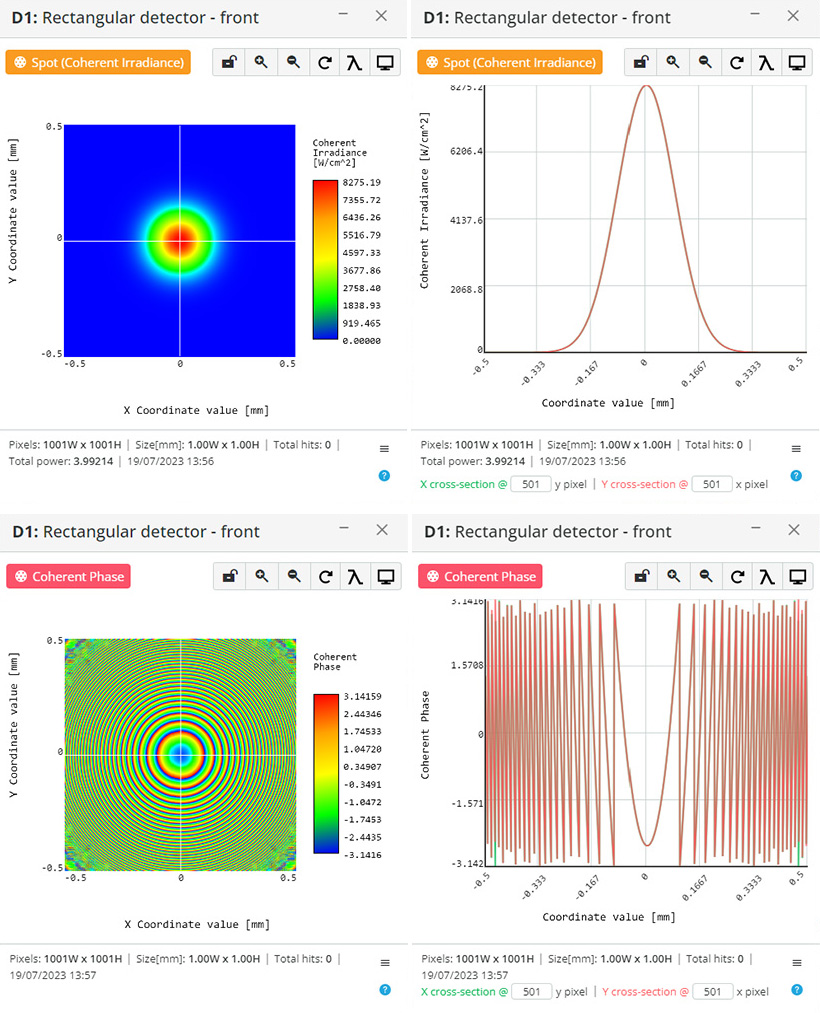
Figure 2 Gaussian beam propagation setup is presented. It consists of a Laser with Gaussian beam waist 0.01 mm, and detector positioned at 10 mm distance from the laser.

Gaussian beams are widely used in optical engineering to model the behavior of light in various optical systems. When light propagates through optical elements such as lenses, mirrors, and waveguides, its interaction can be accurately approximated using Gaussian beam propagation equations. This simplifies the analysis and design process, allowing engineers to predict the beam’s behavior at different points in the system.

The greatest challenge in the design of VR headsets is currently to achieve a very high imaging performance with a high level of wearing comfort at the same time. Thus, the weight and size of the headsets must be reduced. Therefore one focus is to reduce the thickness of the optics as well as the distance between optics and display.