CaF2molar mass

If you are looking for a derivatation which starts at a more fundamental level than that, then you should pick up any textbook on lasers. Any textbook you can find will cover the derivation of the Gaussian modes of a laser beam from the wave/Helmholtz equation. You can also look at section 2.1 of my thesis where I sketch out the derivation from the Helmholtz equation although I stop slightly short of deriving the divergence angle.

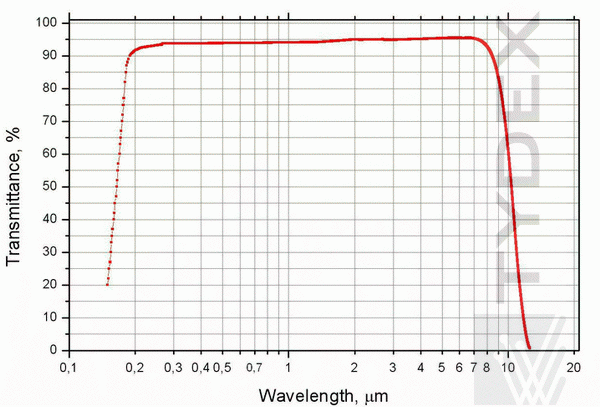
Fig. 1. The measurements were carried out on Perkin Elmer Lambda-35 spectrophotometer and on BrukerVertex-70 Fourier-spectrometer.

CaF2chemical name

CaF2 (Calcium Fluoride) is widespread material for UV and IR spectroscopy from 0.15 to 9 transmission range as well as for laser applications. The crystal is optically isotropic, non-hygrоscopic and insoluble in most acids and alkali therefore the polished surfaces are practically not degraded in normal atmospheric conditions. A high mechanical strength makes it useful for high pressure applications. At the same time it is very sensitive to thermal shock. Low refraction index of CaF2 makes it possible to be used without anti-reflection coating for non-laser applications.

CaF2structure

Please pay your attention that this article is for your information only. We do not supply CaF2 in ingots as well as semi-finished products. Our standard products are polished parts.For further information on our CaF2 optical components please see the following: Windows for IR-spectroscopy, FTIR Beam Splitter, Packaging or fill in our request form.

Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

I will assume that you are asking about laser beams in the fundamental, diffraction limited Gaussian mode. The standard expression for the divergence angle of a Gaussian beam in the far field is (see the Wikipedia page on Gaussian beams) $$ \theta=\frac{\lambda}{\pi\omega_0} $$ where $\omega_0$ is the so-called waist size of the Gaussian beam. From here you can calculate the solid angle subtended by the beam which is given, in the small $\theta$ limit, as $$ \Theta\simeq\pi\theta^2=\frac{\lambda^2}{\pi\omega_0^2}=\frac{\lambda^2}{A}, $$ where $A$ is the area of the beam's waist.