The main advantage of such resonators is that the mode volume in the cavity can be large, which leads to low power densities on the mirrors (for high power lasers, the damage threshold of the mirrors could be easily reached). Moreover, the transverse modes undergo a high level of losses in an unstable resonator, leading to a natural transverse single-mode operation of the laser.

Coherentlight

T can be diagonalized , and if P is the transition matrix and xi the eigenvectors of T, we can show that (see a course on linear algebra).

Collimating lens

A ray bundle, or beam of light, in which every ray is parallel to every other ray of light, which effectively originates from an infinitely small point source located at infinity. Note that light is never perfectly collimated.

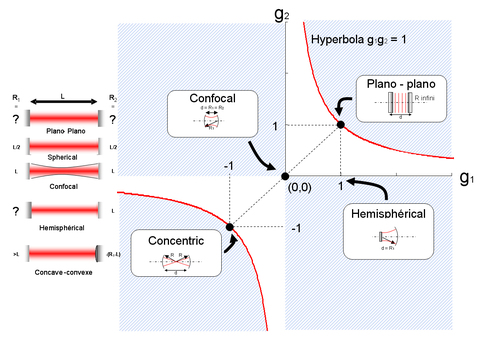
The stability condition is then figured by two hyperboles, and the stability zones are hatched in pale blue on figure 7.

Collimatedbeam divergence

Laser collimation

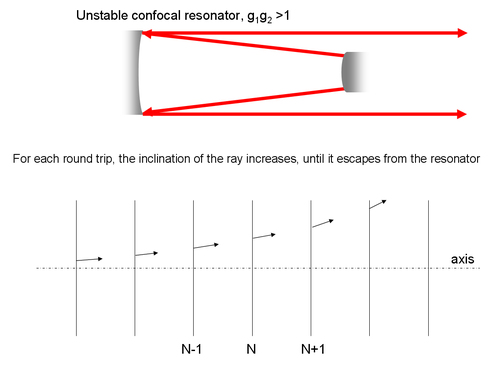
A stable resonator is not a necessary condition to make a laser. In some case, if the laser medium exhibits a gain coefficient high enough to allow a high level of losses, unstable resonators can even be very useful. This is for example the case with very high power lasers.

The resonator is stable if the rays stay in the vicinity of the optical axis during the propagation when n goes to infinity. In other words, pn must have an upper bound, that is and .

Let's d be the length of a simple two-mirrors linear resonator (radii of curvature R1 and R2). This resonator is equivalent to a periodic sequence made of two thin lenses with focal lengthes equal to f1 (=R1/2) and f2 (=R2/2), spaced by a distance d.

Those type of resonators are only possible with very high gain systems, because a given ray passes only a few times inside the amplifying medium before escaping from the cavity.

The straight lines g1=1 et g2=1 correspond to resonators with one plane mirror (infinite radius of curvature). The Fabry-Pérot (plano-plano cavity, that is two plane mirrors) is obtained for g1=g2=1.

Collimatedbeam

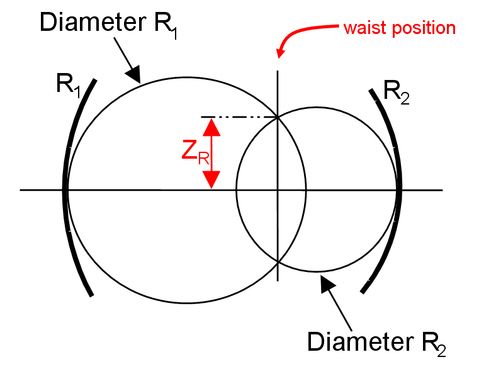
There is a simple graphical method to know if a 2-mirrors resonator is stable or not : the point is to check if two circles (with diameter R1 and R2 respectively) centred on the focal points F1 and F2 have an intersection (see figure 8). If they do, the cavity is stable. Moreover, the circles intersection gives the position of the waist and the Rayleigh length (those two parameters will be defined in an upcoming paragraph)

This relation is often drawn on a diagram representing the g2(g1) space, that is with g2 as y-axis and g1 as x-axis (figure 7).

For n periods, that is n round trips inside the cavity, the transfer matrix is Tn. If we write the vector representing an optical ray at the entrance of a period, and the exit vector, then ,

Copyright 2023, Edmund Optics Inc., 14F., No.83, Sec. 4, Wenxin Road, Beitun District , Taichung City 406, Taiwan (R.O.C.)