This Field of View (FOV) calculator will help you setup your screens for sim racing, giving you a correct feel within the sim that will help you become faster and more consistent. Don't want to read all this? Watch my video on how to setup FOV in iRacing instead! Supported sims: iRacing, more coming soon! If this page or video helped you out, consider donating to my channel, it really helps me out and allows me to continue making these kinds of videos.

Use the differential dzdz to approximate the change in z=4−x2−y2z=4−x2−y2 as (x,y)(x,y) moves from point (1,1)(1,1) to point (1.01,0.97).(1.01,0.97). Compare this approximation with the actual change in the function.

The contrapositive of the preceding theorem states that if a function is not differentiable, then at least one of the hypotheses must be false. Let’s explore the condition that fx(0,0)fx(0,0) must be continuous. For this to be true, it must be true that lim(x,y)→(0,0)fx(0,0)=fx(0,0):lim(x,y)→(0,0)fx(0,0)=fx(0,0):

Find the equation of the tangent plane to the surface defined by the function f(x,y)=2x2−3xy+8y2+2x−4y+4f(x,y)=2x2−3xy+8y2+2x−4y+4 at point (2,−1).(2,−1).

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution-NonCommercial-ShareAlike License and you must attribute OpenStax.

© Jul 25, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Move closer to your screens - if your using a desk and the limiting factor is pedal distance then move your desk away from the wall a few inches. This will keep your pedal distance the same but you will be closer to your monitors. Move your screens closer to you - your screens need to be as close to your wheel as possible Upgrade to bigger screens - 27" is best bang for your buck and look for 1-5ms response time and 144hz if your GPU can push that.

In Linear Approximations and Differentials we first studied the concept of differentials. The differential of y,y, written dy,dy, is defined as f′(x)dx.f′(x)dx. The differential is used to approximate Δy=f(x+Δx)−f(x),Δy=f(x+Δx)−f(x), where Δx=dx.Δx=dx. Extending this idea to the linear approximation of a function of two variables at the point (x0,y0)(x0,y0) yields the formula for the total differential for a function of two variables.

A function f(x,y)f(x,y) is differentiable at a point P(x0,y0)P(x0,y0) if, for all points (x,y)(x,y) in a δδ disk around P,P, we can write

Electrical power PP is given by P=V2R,P=V2R, where VV is the voltage and RR is the resistance. Approximate the maximum percentage error in calculating power if 120120 VV is applied to a 2000−Ω2000−Ω resistor and the possible percent errors in measuring VV and RR are 3%3% and 4%,4%, respectively.

The base radius and height of a right circular cone are measured as 1010 in. and 2525 in., respectively, with a possible error in measurement of as much as 0.10.1 in. each. Use differentials to estimate the maximum error in the calculated volume of the cone.

Khush Enterprises is one of the distributors for First Contact Polymer and stockist in India. This one-part strip coating simplifies your cleaning process.

Replicated Hollow Metal Retroreflectors feature a monolithic design, resulting in return beam accuracy unaffected by vibration.

If a function of three variables is differentiable at a point (x0,y0,z0),(x0,y0,z0), then it is continuous there. Furthermore, continuity of first partial derivatives at that point guarantees differentiability.

Find the differential dzdz of the function f(x,y)=4y2+x2y−2xyf(x,y)=4y2+x2y−2xy and use it to approximate ΔzΔz at point (1,−1).(1,−1). Use Δx=0.03Δx=0.03 and Δy=−0.02.Δy=−0.02. What is the exact value of Δz?Δz?

GLASS CERAMIC MILLING TOOL ; Size: · Dia coated Φ2.0 ; Type: · Ball end mill ; Machine: · DM/DS200-4W(A/X) ; Shank: · Shank 6.

(A, B) A concave (minus) lens is used to correct myopia, in which parallel rays are focused anterior to the macula. (C, D) A convex (plus) lens is.

[T] Find the equation of the tangent plane to the surface z=f(x,y)=sin(x+y2)z=f(x,y)=sin(x+y2) at point (π4,0,22),(π4,0,22), and graph the surface and the tangent plane.

Let P0=(x0,y0,z0)P0=(x0,y0,z0) be a point on a surface S,S, and let CC be any curve passing through P0P0 and lying entirely in S.S. If the tangent lines to all such curves CC at P0P0 lie in the same plane, then this plane is called the tangent plane to SS at P0P0 (Figure 4.27).

If y>0,y>0, then this expression equals 1/(k2+1)3/2;1/(k2+1)3/2; if y<0,y<0, then it equals −(1/(k2+1)3/2).−(1/(k2+1)3/2). In either case, the value depends on k,k, so the limit fails to exist.

Intuitively, it seems clear that, in a plane, only one line can be tangent to a curve at a point. However, in three-dimensional space, many lines can be tangent to a given point. If these lines lie in the same plane, they determine the tangent plane at that point. A tangent plane at a regular point contains all of the lines tangent to that point. A more intuitive way to think of a tangent plane is to assume the surface is smooth at that point (no corners). Then, a tangent line to the surface at that point in any direction does not have any abrupt changes in slope because the direction changes smoothly.

Show that f(x,y)=x2+3yf(x,y)=x2+3y is differentiable at every point. In other words, show that Δz=f(x+Δx,y+Δy)−f(x,y)=fxΔx+fyΔy+ε1Δx+ε2Δy,Δz=f(x+Δx,y+Δy)−f(x,y)=fxΔx+fyΔy+ε1Δx+ε2Δy, where both ε1ε1 and ε2ε2 approach zero as (Δx,Δy)(Δx,Δy) approaches (0,0).(0,0).

Continuity of First Partials Implies Differentiability further explores the connection between continuity and differentiability at a point. This theorem says that if the function and its partial derivatives are continuous at a point, the function is differentiable.

Normal vector of aplane

All of the preceding results for differentiability of functions of two variables can be generalized to functions of three variables. First, the definition:

Find the total differential of the function z=xyy+xz=xyy+x where xx changes from 10to10.510to10.5 and yy changes from 15to13.15to13.

Given a function z=f(x,y)z=f(x,y) with continuous partial derivatives that exist at the point (x0,y0),(x0,y0), the linear approximation of ff at the point (x0,y0)(x0,y0) is given by the equation

The idea behind differentiability of a function of two variables is connected to the idea of smoothness at that point. In this case, a surface is considered to be smooth at point PP if a tangent plane to the surface exists at that point. If a function is differentiable at a point, then a tangent plane to the surface exists at that point. Recall the formula for a tangent plane at a point (x0,y0)(x0,y0) is given by

To see why this formula is correct, let’s first find two tangent lines to the surface S.S. The equation of the tangent line to the curve that is represented by the intersection of SS with the vertical trace given by x=x0x=x0 is z=f(x0,y0)+fy(x0,y0)(y−y0).z=f(x0,y0)+fy(x0,y0)(y−y0). Similarly, the equation of the tangent line to the curve that is represented by the intersection of SS with the vertical trace given by y=y0y=y0 is z=f(x0,y0)+fx(x0,y0)(x−x0).z=f(x0,y0)+fx(x0,y0)(x−x0). A parallel vector to the first tangent line is a=j+fy(x0,y0)k;a=j+fy(x0,y0)k; a parallel vector to the second tangent line is b=i+fx(x0,y0)k.b=i+fx(x0,y0)k. We can take the cross product of these two vectors:

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

As the wound heals and skin regrows, the treated area is smoother and tighter. Types of ablative lasers include carbon dioxide (CO2) lasers, erbium lasers and ...

Given the function f(x,y)=41−4x2−y2,f(x,y)=41−4x2−y2, approximate f(2.1,2.9)f(2.1,2.9) using point (2,3)(2,3) for (x0,y0).(x0,y0). What is the approximate value of f(2.1,2.9)f(2.1,2.9) to four decimal places?

( x 2 + y 2 ) 2 = 9 ( x 2 − y 2 ) , P ( 2 , 1 ) ( x 2 + y 2 ) 2 = 9 ( x 2 − y 2 ) , P ( 2 , 1 )

The last term in Equation 4.26 is referred to as the error term and it represents how closely the tangent plane comes to the surface in a small neighborhood (δ(δ disk) of point P.P. For the function ff to be differentiable at P,P, the function must be smooth—that is, the graph of ff must be close to the tangent plane for points near P.P.

The centripetal acceleration of a particle moving in a circle is given by a(r,v)=v2r,a(r,v)=v2r, where vv is the velocity and rr is the radius of the circle. Approximate the maximum percent error in measuring the acceleration resulting from errors of 3%3% in vv and 2%2% in r.r. (Recall that the percentage error is the ratio of the amount of error over the original amount. So, in this case, the percentage error in aa is given by daa.)daa.)

Differentiability Implies Continuity shows that if a function is differentiable at a point, then it is continuous there. However, if a function is continuous at a point, then it is not necessarily differentiable at that point. For example,

For the following exercises, find parametric equations for the normal line to the surface at the indicated point. (Recall that to find the equation of a line in space, you need a point on the line, P0(x0,y0,z0),P0(x0,y0,z0), and a vector n=〈a,b,c〉n=〈a,b,c〉 that is parallel to the line. Then the equation of the line is x−x0=at,y−y0=bt,z−z0=ct.)x−x0=at,y−y0=bt,z−z0=ct.)

tangent plane中文

For a tangent plane to a surface to exist at a point on that surface, it is sufficient for the function that defines the surface to be differentiable at that point, defined later in this section. We define the term tangent plane here and then explore the idea intuitively.

This vector is perpendicular to both lines and is therefore perpendicular to the tangent plane. We can use this vector as a normal vector to the tangent plane, along with the point P0=(x0,y0,f(x0,y0))P0=(x0,y0,f(x0,y0)) in the equation for a plane:

Let z=f(x,y)z=f(x,y) be a function of two variables with (x0,y0)(x0,y0) in the domain of f.f. If f(x,y),f(x,y), fx(x,y),fx(x,y), and fy(x,y)fy(x,y) all exist in a neighborhood of (x0,y0)(x0,y0) and are continuous at (x0,y0),(x0,y0), then f(x,y)f(x,y) is differentiable there.

[T] Find the equation for the tangent plane to the surface at the indicated point, and graph the surface and the tangent plane: z=ln(10x2+2y2+1),P(0,0,0).z=ln(10x2+2y2+1),P(0,0,0).

[T] Find the equation of the tangent plane to the surface f(x,y)=x2+y2f(x,y)=x2+y2 at point (1,2,5),(1,2,5), and graph the surface and the tangent plane at the point.

The tangent line can be used as an approximation to the function f(x)f(x) for values of xx reasonably close to x=a.x=a. When working with a function of two variables, the tangent line is replaced by a tangent plane, but the approximation idea is much the same.

When working with a function y=f(x)y=f(x) of one variable, the function is said to be differentiable at a point x=ax=a if f′(a)f′(a) exists. Furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners exist) and a tangent line is well-defined at that point.

First, we calculate f(x0,y0),fx(x0,y0),andfy(x0,y0)f(x0,y0),fx(x0,y0),andfy(x0,y0) using x0=2x0=2 and y0=−3,y0=−3, then we use Equation 4.26:

The function f(x,y)={xyx2+y2(x,y)≠(0,0)0(x,y)=(0,0)f(x,y)={xyx2+y2(x,y)≠(0,0)0(x,y)=(0,0) is not differentiable at the origin. We can see this by calculating the partial derivatives. This function appeared earlier in the section, where we showed that fx(0,0)=fy(0,0)=0.fx(0,0)=fy(0,0)=0. Substituting this information into Equation 4.26 using x0=0x0=0 and y0=0,y0=0, we get

Compressed Air Dusters at Office Depot & OfficeMax. Shop today online, in store or buy online and pick up in stores.

A function f(x,y,z)f(x,y,z) is differentiable at a point P(x0,y0,z0)P(x0,y0,z0) if for all points (x,y,z)(x,y,z) in a δδ disk around PP we can write

See the preceding problem. Use differentials to estimate the volume of aluminum in an enclosed aluminum can with diameter 8.0cm8.0cm and height 12cm12cm if the aluminum is 0.040.04 cm thick.

Tangentplaneand normal line

Notice that the symbol ∂∂ is not used to denote the total differential; rather, dd appears in front of z.z. Now, let’s define Δz=f(x+Δx,y+Δy)−f(x,y).Δz=f(x+Δx,y+Δy)−f(x,y). We use dzdz to approximate Δz,Δz, so

Find the equation of the tangent plane to the surface defined by the function f(x,y)=sin(2x)cos(3y)f(x,y)=sin(2x)cos(3y) at the point (π/3,π/4).(π/3,π/4).

The electrical resistance RR produced by wiring resistors R1R1 and R2R2 in parallel can be calculated from the formula 1R=1R1+1R2.1R=1R1+1R2. If R1R1 and R2R2 are measured to be 7Ω7Ω and 6Ω,6Ω, respectively, and if these measurements are accurate to within 0.05Ω,0.05Ω, estimate the maximum possible error in computing R.R. (The symbol ΩΩ represents an ohm, the unit of electrical resistance.)

The period TT of a simple pendulum with small oscillations is calculated from the formula T=2πLg,T=2πLg, where LL is the length of the pendulum and gg is the acceleration resulting from gravity. Suppose that LL and gg have errors of, at most, 0.5%0.5% and 0.1%,0.1%, respectively. Use differentials to approximate the maximum percentage error in the calculated value of T.T.

When x>0,x>0, the slope of this curve is equal to 2/2;2/2; when x<0,x<0, the slope of this curve is equal to −(2/2).−(2/2). This presents a problem. In the definition of tangent plane, we presumed that all tangent lines through point PP (in this case, the origin) lay in the same plane. This is clearly not the case here. When we study differentiable functions, we will see that this function is not differentiable at the origin.

If the second polarisation direction is at 90 to the original polarisation direction, the arrangement is known as "crossed polars" and the second polariser is ...

I got the Ultrasonic cleaner mainly to clean PCBs or water damaged circuit boards. However, I decided to test how well the cleaner will be able to clean rust ...

In this section, we consider the problem of finding the tangent plane to a surface, which is analogous to finding the equation of a tangent line to a curve when the curve is defined by the graph of a function of one variable, y=f(x).y=f(x). The slope of the tangent line at the point x=ax=a is given by m=f′(a);m=f′(a); what is the slope of a tangent plane? We learned about the equation of a plane in Equations of Lines and Planes in Space; in this section, we see how it can be applied to the problem at hand.

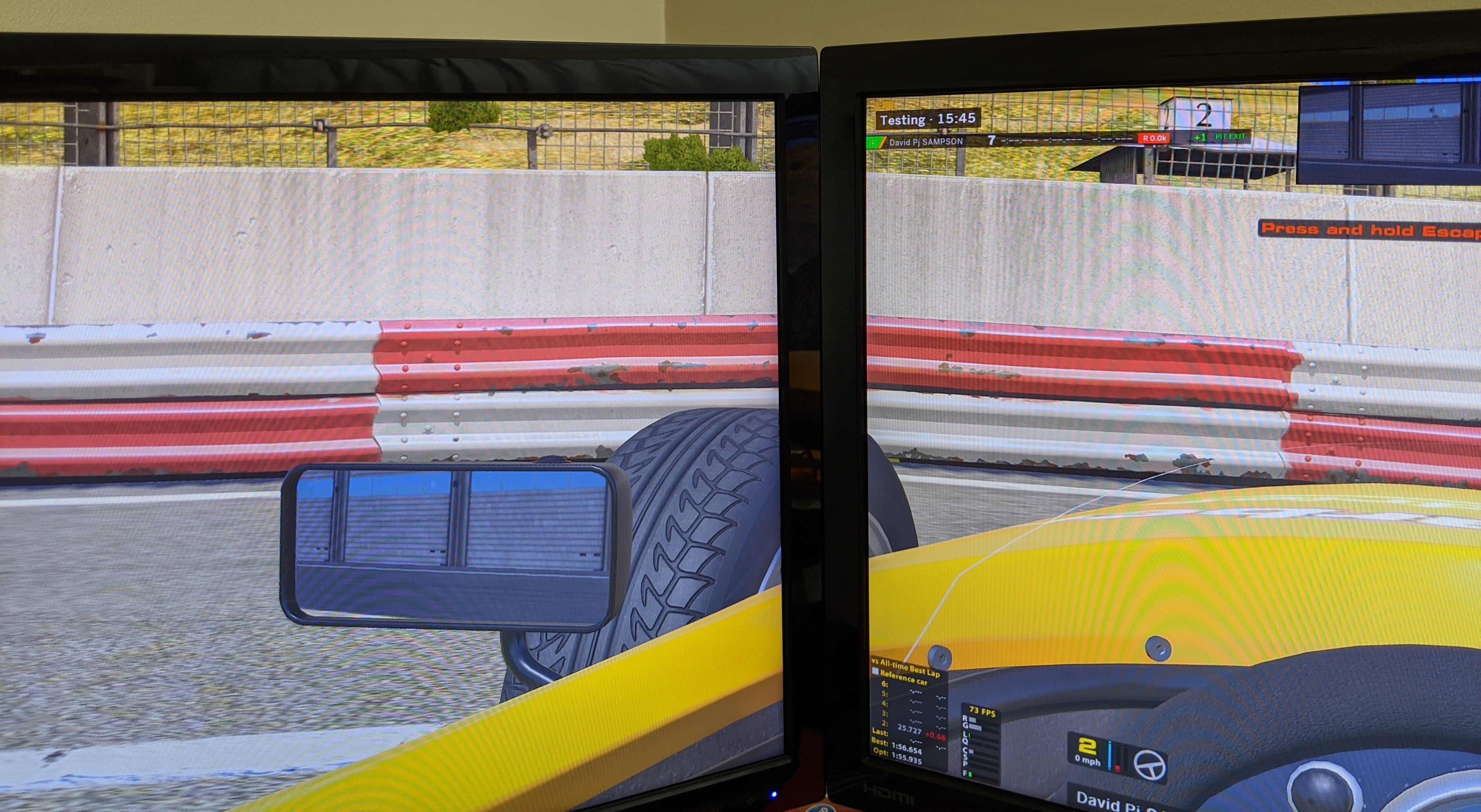
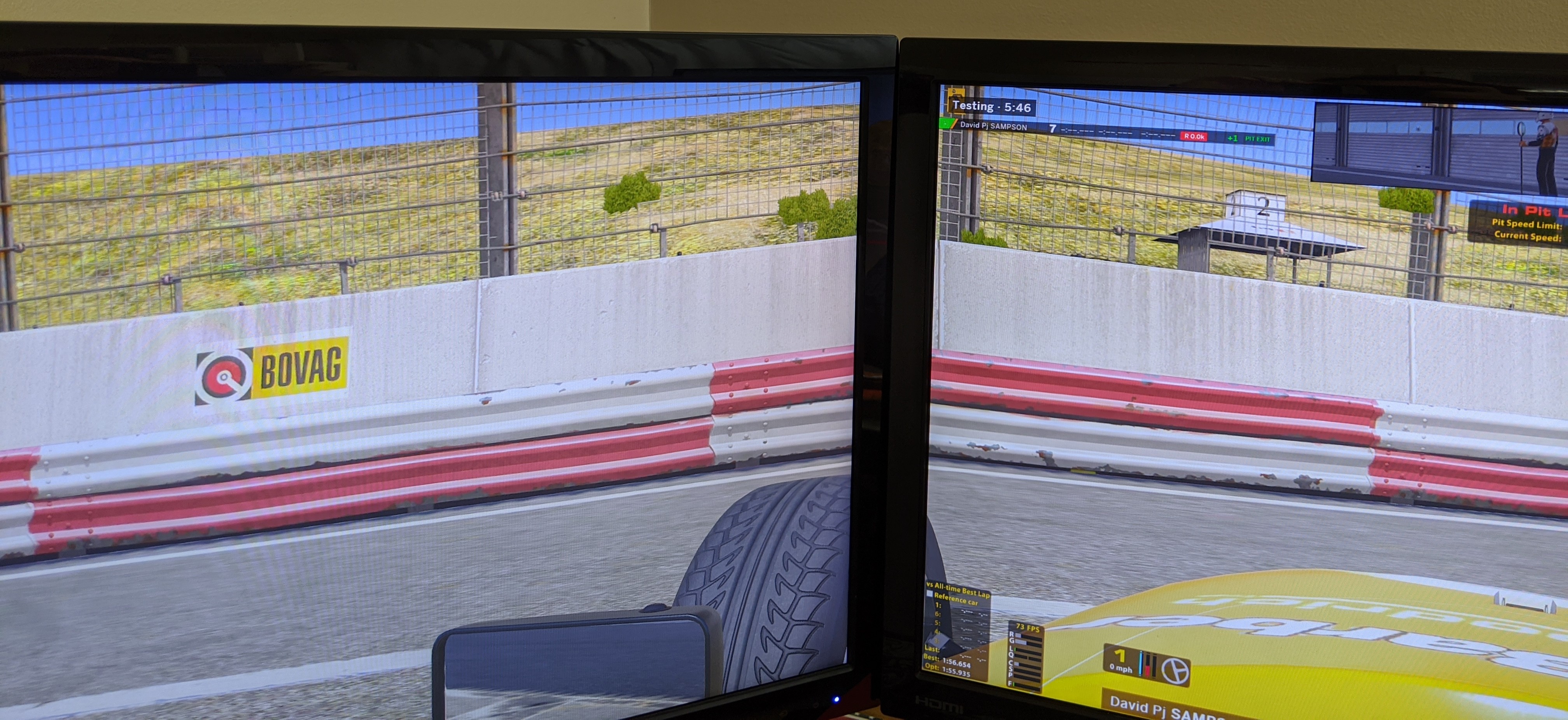
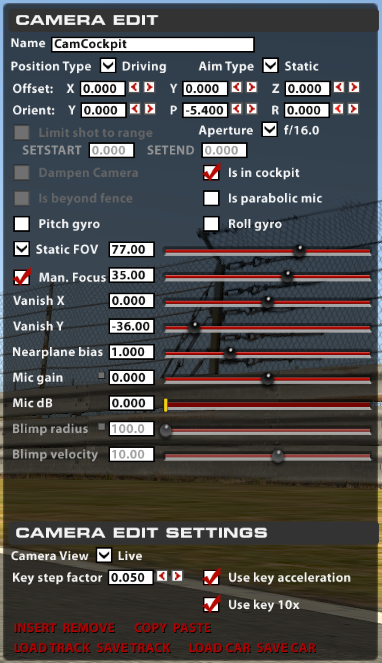
Now we will adjust the driver head rotation (Orient P). Use this same halved number and multiply it by 0.3, this will give you the driver head rotation number. This will align the monitors to the original number that made your monitors straight, but also keep the driver's eye line to the horizon.

Price (Low to High), Price (High to Low). tuneFilters (0). ‹ 1; 2 · 3 · 4 · 5 · › · keyboard_arrow_left. 1 - 20 of 271. keyboard_arrow_right · Angle Bracket ...

Given the function f(x,y)=e5−2x+3y,f(x,y)=e5−2x+3y, approximate f(4.1,0.9)f(4.1,0.9) using point (4,1)(4,1) for (x0,y0).(x0,y0). What is the approximate value of f(4.1,0.9)f(4.1,0.9) to four decimal places?

For the following exercises, find the equation for the tangent plane to the surface at the indicated point. (Hint: Solve for zz in terms of xx and y.)y.)

The volume of a right circular cylinder is given by V(r,h)=πr2h.V(r,h)=πr2h. Find the differential dV.dV. Interpret the formula geometrically.

Depending on the path taken toward the origin, this limit takes different values. Therefore, the limit does not exist and the function ff is not differentiable at the origin as shown in the following figure.

For the following exercises, as a useful review for techniques used in this section, find a normal vector and a tangent vector at point P.P.

One such application of this idea is to determine error propagation. For example, if we are manufacturing a gadget and are off by a certain amount in measuring a given quantity, the differential can be used to estimate the error in the total volume of the gadget.

Let z=f(x,y)z=f(x,y) be a function of two variables with (x0,y0)(x0,y0) in the domain of f.f. If f(x,y)f(x,y) is differentiable at (x0,y0),(x0,y0), then f(x,y)f(x,y) is continuous at (x0,y0).(x0,y0).

Recall from Linear Approximations and Differentials that the formula for the linear approximation of a function f(x)f(x) at the point x=ax=a is given by

Find the differential dzdz of the function f(x,y)=3x2−2xy+y2f(x,y)=3x2−2xy+y2 and use it to approximate ΔzΔz at point (2,−3).(2,−3). Use Δx=0.1Δx=0.1 and Δy=−0.05.Δy=−0.05. What is the exact value of Δz?Δz?

is continuous at the origin, but it is not differentiable at the origin. This observation is also similar to the situation in single-variable calculus.

To apply Equation 4.25, we first must calculate f(x0,y0),f(x0,y0), fx(x0,y0),fx(x0,y0), and fy(x0,y0)fy(x0,y0) using x0=2x0=2 and y0=3:y0=3:

Once you have the above set in iRacing correctly and you have made sure your monitor angles match the above angle, you now need to make sure your horizon is set correctly, based on your height against your monitors. This will prevent warping on your side monitors.

Let SS be a surface defined by a differentiable function z=f(x,y),z=f(x,y), and let P0=(x0,y0)P0=(x0,y0) be a point in the domain of f.f. Then, the equation of the tangent plane to SS at P0P0 is given by

If either x=0x=0 or y=0,y=0, then f(x,y)=0,f(x,y)=0, so the value of the function does not change on either the x- or y-axis. Therefore, fx(x,0)=fy(0,y)=0,fx(x,0)=fy(0,y)=0, so as either xoryxory approach zero, these partial derivatives stay equal to zero. Substituting them into Equation 4.24 gives z=0z=0 as the equation of the tangent line. However, if we approach the origin from a different direction, we get a different story. For example, suppose we approach the origin along the line y=x.y=x. If we put y=xy=x into the original function, it becomes

Notice that this equation also represents the tangent plane to the surface defined by z=f(x,y)z=f(x,y) at the point (x0,y0).(x0,y0). The idea behind using a linear approximation is that, if there is a point (x0,y0)(x0,y0) at which the precise value of f(x,y)f(x,y) is known, then for values of (x,y)(x,y) reasonably close to (x0,y0),(x0,y0), the linear approximation (i.e., tangent plane) yields a value that is also reasonably close to the exact value of f(x,y)f(x,y) (Figure 4.31). Furthermore the plane that is used to find the linear approximation is also the tangent plane to the surface at the point (x0,y0).(x0,y0).

Since E(x,y)≥0E(x,y)≥0 for any value of xory,xory, the original limit must be equal to zero. Therefore, f(x,y)=2x2−4yf(x,y)=2x2−4y is differentiable at point (2,−3).(2,−3).

Find the equation of the tangent plane to the surface defined by the function f(x,y)=x3−x2y+y2−2x+3y−2f(x,y)=x3−x2y+y2−2x+3y−2 at point (−1,3).(−1,3).

f ( x , y , z ) = x 2 + y 2 + z 2 , P ( 3 , 2 , 6 ) f ( x , y , z ) = x 2 + y 2 + z 2 , P ( 3 , 2 , 6 )

Let z=f(x,y)z=f(x,y) be a function of two variables with (x0,y0)(x0,y0) in the domain of f,f, and let ΔxΔx and ΔyΔy be chosen so that (x0+Δx,y0+Δy)(x0+Δx,y0+Δy) is also in the domain of f.f. If ff is differentiable at the point (x0,y0),(x0,y0), then the differentials dxdx and dydy are defined as

Differentiability and continuity for functions of two or more variables are connected, the same as for functions of one variable. In fact, with some adjustments of notation, the basic theorem is the same.

My best tip is to jump in a car and open up the camera tools (CTRL F12). Adjust the Vanish Y, until everything across all monitors looks straight. Once you have a number that works, set only half of that number to Vanish Y.

Let z=f(x,y)=xey.z=f(x,y)=xey. Compute ΔzΔz from P(1,2)P(1,2) to Q(1.05,2.1)Q(1.05,2.1) and then find the approximate change in zz from point PP to point Q.Q. Recall Δz=f(x+Δx,y+Δy)−f(x,y),Δz=f(x+Δx,y+Δy)−f(x,y), and dzdz and ΔzΔz are approximately equal.

Let z=f(x,y)=x2+3xy−y2.z=f(x,y)=x2+3xy−y2. Find the exact change in the function and the approximate change in the function as xx changes from 2.00to2.052.00to2.05 and yy changes from 3.00to2.96.3.00to2.96.

Therefore, the differential is used to approximate the change in the function z=f(x0,y0)z=f(x0,y0) at the point (x0,y0)(x0,y0) for given values of ΔxΔx and Δy.Δy. Since Δz=f(x+Δx,y+Δy)−f(x,y),Δz=f(x+Δx,y+Δy)−f(x,y), this can be used further to approximate f(x+Δx,y+Δy):f(x+Δx,y+Δy):

Since its inception in 1948, various Harvard departments and private benefactors have added material to the original nucleus of the Collection of Historical ...

The radius rr and height hh of a right circular cylinder are measured with possible errors of 4%and5%,4%and5%, respectively. Approximate the maximum possible percentage error in measuring the volume (Recall that the percentage error is the ratio of the amount of error over the original amount. So, in this case, the percentage error in VV is given by dVV.)dVV.)

For a tangent plane to exist at the point (x0,y0),(x0,y0), the partial derivatives must therefore exist at that point. However, this is not a sufficient condition for smoothness, as was illustrated in Figure 4.29. In that case, the partial derivatives existed at the origin, but the function also had a corner on the graph at the origin.