In fact, up to now, before our innovative solution described below, optimal 3D results could only be obtained using dedicated real 3D scanners based on a Laser or confocal sensor and, therefore, by scanning the originals one point after the other (the full scan may require hours or even days); but apart from the scanning time there are anyway limitations with those kinds of 3D scanners as they usually cannot acquire color information too (only 3D), have limited depth of field and may have also problem on scanning glossy materials.

Photometric stereosoftware

After a long development at METIS, we have been capable of solving those issues through our patented lighting system (the DC SynchroLight) and by writing our own algorithms that implement the Photometric Stereo theoretical model into something that actually works and produce real and consistent results.

Linearly polarized light is a special case of elliptically polarized light.  If the light is linearly polarized, then the two components oscillate in phase,  for example Ex = E0xexp(i(kz - ωt)), Ey = E0yexp(i(kz - ωt)), φ = 0.  The direction of E and the direction of propagation define a plane.  The electric vector traces out a straight line.  For example, E = Ei = E0xexp(i(kz - ωt))i.

photometricstereo中文

The electric field vector E can always be resolved into two perpendicular components.  The light is elliptically polarized, then the two components have a constant phase difference, and the tip of the electric field vector traces out an ellipse in the plane perpendicular to the direction of propagation.

Github robustphotometric Stereovia Low Rank Matrix Completion and Recovery

Thanks to its unique characteristics, METIS 3D provides many advantages over existing 3D laser/confocal scanners such as:

A half-wave plate δ = π can be used to rotate the plane of linearly polarized light.  The angle of rotation is 2θ, where θ is the angle between the angle of polarization and the wave plate's fast axis.

The theory behind Photometric Stereo have been presented for the first time in the 1980, but limited practical use was possible at this time because the provided mathematical model was not adequate for dealing with real-life situation. And in fact, still today Photometric Stereo have limited practical applications because of the very complicated math and because it poses strict design constrain that are very difficult to achieve (i.e. it requires a specific and extremely accurate control over the emitted light rays within the entire scanner optical path).

Photometric stereogithub

In the Glan-Taylor polarizing prism shown on the right the rejected (ordinary) ray is absorbed by black mounting material in the prism housing.

Lambertian surface

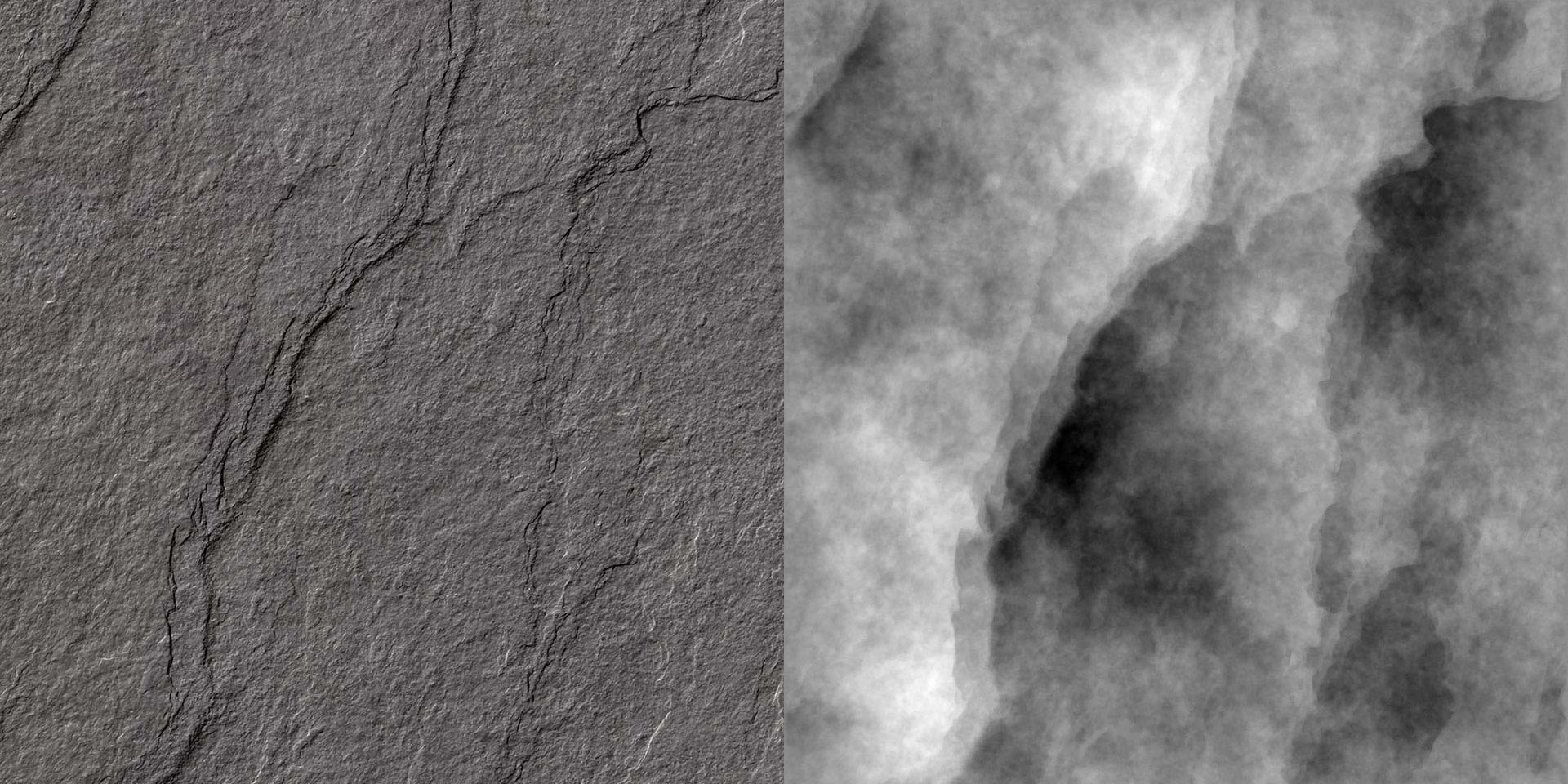
METIS 3D is based on a completely different technology called Photometric Stereo which allows to calculate 3D data directly from 2D color data!

When the sun is at a low angle in the sky, the sunlight reflecting off the surface of water is nearly 100% horizontally polarized because the angle of incidence is close to the Brewster angle.  Glare-reducing sunglasses are coated with a polarizer with a vertical transmission axis and therefore block the reflected light.

A quarter-wave plate δ = π/2 can be used to convert linearly polarized light to circularly polarized light.  The incident linearly polarized light must be oriented at 45o to the wave plate's axes.  A half-wave plate δ = π can be used to rotate the plane of linearly polarized light.  The angle of rotation is 2θ, where θ is the angle between the angle of polarization and the wave plate's fast axis.

Read more about the exclusive METIS Photometric Stereo 3D digitizing technique in this article of Marcus Timson,  The Industrial Print Blog

Photometry

Photometric stereopython

Nowadays, in most applications (e.g. for industrial decor applications, but also for fine art reproduction), it is very important not only to capture color or a visual 3D appearance, but also to be able to calculate 3D data.

LambertianPhotometric Stereo

If a beam of linearly polarized monochromatic light enters a birefringent crystal along a direction not parallel to the optical axis of the crystal, the beam will may be divided into two separate beams.  Each will be polarized at right angles to the other, and they will travel in different directions.  The intensity of the original beam will be divided between the two new beams in a manner which depends on the original orientation of the electric field vector with respect to the crystal.  The ratio or the intensities of the two orthogonally polarized beams can have any value.

Many different technologies are currently available for the real 3D scanning of objects but only a few can be effectively used for the 3D scanning of embossed surfaces (e.g. wood, stones, wallpapers, paintings, etc.). This is because 3D surface scanning for industrial or decorative applications requires very high-resolution levels and also large formats that cannot be achieved using commercial 3D scanning technologies.

Read more about the exclusive METIS Photometric Stereo 3D digitizing technique in this article of Marcus Timson, The Industrial Print Blog

In other devices the changes in direction of propagation between the two rays is used to separate the incoming beam into two orthogonally polarized beams as in the Wollaston and Thompson beam-splitting prisms.

The extraordinary ray violates both Snell’s Law and the Law of Reflection.  It is not necessarily confined to the plane of incidence.  Its speed changes with direction.  The index of refraction for the extraordinary ray is a continuous function of direction.  The index of refraction for the ordinary ray is independent of direction.  When the ordinary index of refraction is plotted against wavelength, the dispersion curve for the ordinary ray is a single unique curve.  The dispersion curve for the extraordinary ray is a family of curves with different curves for different directions.  A ray normally incident on a birefringent crystalline surface will be divided into two rays at the boundary, unless it is in a special polarization state or unless the crystalline surface is perpendicular to an optic axis.  The extraordinary ray will deviate from the incident direction while the ordinary ray will not.  The ordinary ray index n0 and the most extreme extraordinary ray index ne are together known as the principal indices of refraction of the material.  The direction of the lesser index is called the fast axis because light polarized in that direction has the higher speed.

The figure below shows the trace of the field vector Ex = E0exp(i(kz - ωt)), Ey = E0exp(i(kz - ωt + φ)) in a plane perpendicular to the z-axis when looking towards the source.  (E0x = E0y = E0)

The two beams within the birefringent crystal are referred to as the ordinary and extraordinary ray, respectively.  The polarization of the extraordinary ray lies in the plane containing the direction of propagation and the optic axis, and the polarization of the ordinary ray is perpendicular to this plane.