Where as the light emitted by diffuse or exposed light sources always has an effect on the entire space, in the case of tightly controlled light, the effect of the light relates directly to the position of the luminaire.

If we view a sphere under completely diffuse light we cannot perceive its spatial form. It appears to be no more than a circular area. Only when directed light falls on the sphere – i.e. when shadows are created, can we recognise its spatial quality.

Exercise for the reader: Can you use ray tracing to demonstrate the lens equation geometrically? You'll probably need to use similar triangles. Remember, that the lens equation is the relationship between the focal length of the lens, the object distance, and the image distance:$ {1 \over S_o} + {1 \over S_i} = {1\over f} $

In offices, reflections on clear plastic sleeves, computer monitors or glossy paper are not interpreted as information (brilliance), but as disturbing glare, disturbing as it is felt that the information we require is being concealed behind the reflections.

Tell us what you're thinking. We care about your opinion! Please keep in mind that comments are moderated and rel="nofollow" is in use. So, please do not use a spammy keyword or a domain as your name, or it will be deleted. Let's have a professional and meaningful conversation instead. Thanks for dropping by!

When light reflects, the angle of the reflected ray is equal to the angle of the incident ray: $ \theta_r=\theta_i $. Both angles are measured relative to a vector normal to the surface. Incident and reflected rays are in the same plane.

Using the equation we derived earlier to find the image position after light passes through one spherical boundary, we can apply the formula twice--once for each spherical boundary of a simple lens, to calculate where the image will form after light passes through the entire lens. If we maintain our thin lens approximation, and take the image from the first refraction as the object for the second one, we can derive the lens maker's formula:

Note that Snell's law implies that light passing from a medium of lower index to a higher index of refraction ($ n_t > n_i $) bends toward the surface normal ($ \theta_t < \theta_i $), whereas light traveling from a higher index to a lower index of refraction bends away from the normal. Remember, a higher index means a lower velocity of light in the medium.

Perhaps the most fundamental solution to Maxwell's equations is the spherical wave, in which light propagates from a point in space uniformly in all directions. It's called a spherical wave because all points at an equal distance from the source — on the surface of a sphere — have the same magnitude electric (and magnetic) field at every point in time. The ray representation of a spherical wave is just a bunch of arrows with their tails on the source and their heads pointing outward, as shown in figure Figure 1. (Most ray diagrams yourepresent a two-dimensional slice of space.) Since the source is isotropic, it's okay draw a ray in pretty much any direction you feel like. In most cases, certain rays are more helpful for understanding a system than others.

Diffused Lightfor Room

When an object gives off its own light (like a light bulb) or is illuminated, we can imagine that the object is made up of many point sources, where each point on the object is emitting or scattering light in all directions. After refraction, all the rays from a single point in the object plane reach the same location in the image plane, forming an image. The image can be either real or virtual. A real image is one that can be seen if you put a screen on the image plane. A virtual image cannot be seen if a screen is at the image plane since there is no place the rays actually come together; it needs another lens (such as your eye) in order to view it. More examples of real and virtual images are described in a following section.

Having dealt with light quantity, conside-ration must be given to the quality of light, the difference between diffuse light and directed light being one of the most important aspects. We are familiar with these different forms of light through our everyday experience with daylight – direct sunlight when the sky is clear and diffuse light when the sky is overcast.

Diffused lightarchitecture

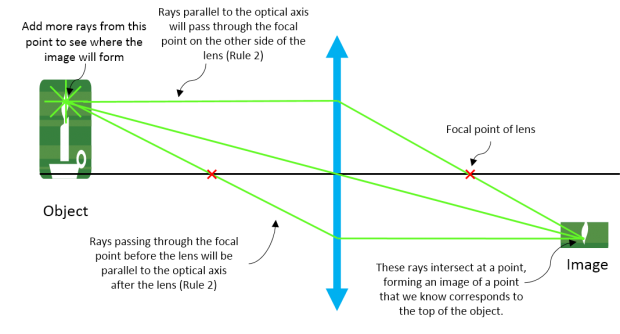
As we begin to deal with multiple boundaries, it can become complicated to solve many geometric equations to find where the image will form. In order to make more tractable calculations for us to use when designing our optical systems, we rely on a few first-order, or Gaussian optics, approximations:

In some standards for workplace lighting there is a criterion for the modelling effect of a lighting installation. It is referred to as the modelling factor, which is defined as the ratio of cylindrical illuminance to horizontal illuminance. When planning the application of directed and diffuse light it is advisable to rely on our fundamental experience of daylight with regard to the direction and colour of the light.

Another fundamental solution to Maxwell's equation is the plane wave. In plane waves, the electric field has the same magnitude in all planes perpendicular to the direction of propagation. Conceptually, a plane wave propagating in the z direction is generated by an infinite number of identical, in-phase point sources uniformly distributed in a plane at $ z=-\infty $. Wavefront and ray representations of the plane wave are shown in Figure Figure 2. Plane waves are a useful model for some circumstances, but real plane waves cannot be generated because of their infinite extent (which means a real plane wave would require an infinite amount of power).

The simplifications of ray optics provide a very good way to understand systems of lenses, mirrors, filters, and illumination sources. In many cases, ray optics can elucidate the function of a complicated optical system with just a few lines, triangles, and simple rules. Of course, the simplicity of ray optics comes at a cost. Ray optics glosses over important details like diffraction. Because the fine details are omitted, ray optics alone does not provide insight into detailed performance characteristics of an optical system like resolution. Diffraction and resolution and optical aberrations (which cause simplifying assumptions fail) are discussed on separate pages.

Your friend is building an endoscope, where she wants to faithfully extend an image across a long distance. She proposes a system composed of two convex lenses having the same focal length (f) shown below.

Only through directed light are we able to gain information about the three-dimensional character of objects. Just as it is impossible for us to retrieve this information when there is no directed light at all, too much shaping can conceal information. This happens when intensely directed light casts such stark shadows that parts of an object are concealed by the darkness.

Note the sign convention is that if $ S_i < 0 $, the light diverges, and a virtual image is formed at a distance $ |S_i| $ in front of the lens, on the same side of the lens as the light source (virtual images will be discussed more in a following section).

Light is an extraordinarily complicated, three dimensional, time dependent phenomenon. There are two predominant theoretical models of light: the wave (or classical) theory and the quantum theory. In the wave theory, light is modeled as a time-varying electric and magnetic field. Completely describing a light field requires specifying the intensity, phase, and direction of the electric and magnetic field at every point in space and time. In the quantum model, light is composed of discrete energy packets with probabilistic behavior. Neither model makes it particularly easy to conceptualize how a pair of binoculars or a microscope works. Fortunately, there is a simplified model of light called ray optics that works well in situations where the objects that interact with a light field are much larger than the wavelength of the light. Ray optics (also called geometrical optics) represents a light field as a bunch of arrows that point in the direction of propagation. Rays begin at a source and go straight, until an interaction between light and matter causes a change.

Using this relationship, you can see why light going through a converging lens can produce three different results (this is similar to what we saw earlier for light passing through a spherical boundary). Whether the light converges, diverges, or is collimated depends on where the object is relative to the focal length of the lens:

Save 50% on all EEP Academy courses with Enterprise Membership Plan and study specialized LV/MV/HV technical articles & guides.

This can be exploited for dramatic effects through accent lighting. This technique is often applied for the presentation of objects, but is only used in architectural lighting when the concept intends to create a dramatic spatial effect.

Based on what we've learned about how light is redirected when passing through lenses, we can come up with a set of rules to simplify our analysis of optical systems. With the technique of ray tracing, we can figure out where images are formed, whether they're upside down, magnified, etc.

Directed light is emitted from point light sources. In the case of daylight this is the sun,in artificial lighting compact light sources. The essential properties of directed light are the production of shadows on objects and structured surfaces, and reflections on specular objects. These effects are particularly noticeable when the general lighting consists of only a small portion of diffuse light.

Directed light can also be applied with sparkling effect for the presentation of specific objects – making them appear more precious. This applies above all for the presentation of refractive or shiny materials, i.e. glass, ceramics, paint or metal. Brilliance is effective because it attracts our attention with the promise of information content. The information we receive may only be that there is a sparkling light source.

But it may also be information regarding the type and quality of a surface, through the geometry and symmetry of the reflections.

Here lies one of the most progressive aspects of lighting technology. Whereas in the era of the candle and the oil lamp the light was bound to the immediate vicinity of the luminaire, it is now possible to use light in other parts of the space at any distance from where the light source is located.

Let's use ray tracing to walk through a few examples of real and virtual images. In these examples we will consider the lens of your eye and the image formed on the retina.

Light incident at an interface between two media will be partly reflected back into the first medium and partly transmitted to the second medium. The speed of light will be different in the two media based on their material properties. The index of refraction $ n $ for each material is defined as the ratio of the speed of light in vacuum, $ c $, by the speed of light in the medium $ v $. More succinctly, $ n = c / v $. When the light changes speed in the second medium, its direction of propagation also changes. This phenomenon is known as refraction. The transmitted light propagates at an angle described by Snell's law:

The light source itself will be seen as a brilliant point of light. A good example of this is the effect of a candlelight in evening light. Objects that refract this light are perceived as specular, e.g. illuminated glass, polished gems or crystal chandeliers. Brilliance is also produced when light falls on highly glossy surfaces, such as porcelain, glass, paint or varnish, polished metal or wet materials.

What isdiffused lightfor plants

A practical note: to minimize spherical aberrations, the general rule is to position the curved side of the lens toward the collimated/straight light.

This formula shows us that the focal length of the lens is a characteristic of the lens, based on its radii of curvature and relevant indices of refraction.

Daylight, for example, has a more or less fixed ratio of sunlight to sky light (directed light to diffuse light) of 5:1 to 10:1. In interior spaces, on the other hand, we can determine the ratio of directed and diffuse light we require or prefer.

Another basic feature of the world around us, and one that we take absolutely for granted, is its three-dimensional quality.

Diffused lightceiling

Say you're building a microscope and you want to expand the coverage of light that is illuminating your sample. You decide you want to build a beam expander to accomplish this. Assume that the incident light is collimated and you want the resulting light from your beam expander to also be collimated. Come up with two ways to make a beam expander using only two lenses each time--one way with two converging lenses, and another way with one converging and one diverging lens. For each system, answer the following questions:

Brilliance can be a means of attracting attention to the light source, lending a space an interesting, lively character.

Diffusedlighting interior design

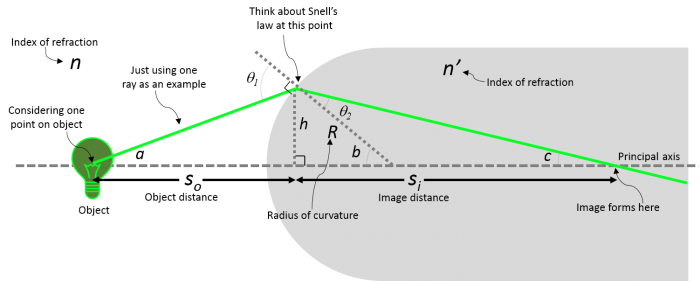
The figure below demonstrates how light rays from a point on an object (the light bulb) can focus to a point after passing through a spherical boundary. The depicted angles and defined lengths can be used to calculate where the light will focus. Even though we only pick a few rays to look at, remember that each point on the object acts as a point source where there are light rays emanating from them in all directions.

It is, of course, possible to apply light from other directions and with other colour temperature combinations, but this will lead to effects that are especially striking or strange.

Lenses are one of the most common components of optical instruments. There are many types of lenses, but the most common ones are spherical lenses, which have curved surfaces. To better understand how they manipulate light, let's consider what happens to light at a spherical boundary.

After reading this page and working through the example optical systems, you should be able to use ray optics to understand the function of many optical systems that you encounter or desire to build.

Direct sunlight either comes from above or from the side, but never from below. The colour of sunlight is clearly warmer than that of diffuse sky light. Consequently, lighting that comprises directed light falling diagonally from above with a lower colour temperature than the diffuse general lighting will be felt to be natural.

The task of lighting design is therefore to create a suitable ratio of diffuse light to directed light to meet the requirements of each individual situation. Specific visual tasks, where the spatial quality or the surface structure is of prime importance, require lighting that emphasises shapes and forms. Only in situations where spatial quality and surface structure are of no importance, or if they are disturbing factors, can completely diffuse lighting be used.

When applied to the lighting of objects brilliance accentuates their spatial quality and surface structure – similar to modelling – because sparkling effects are mainly evident along edges and around the curves on shiny objects.

Let's put two spherical interfaces together to make a spherical lens. Each lens consists of two spherical interfaces with radii of curvature $ R_1 $ and $ R_2 $. Its focal length $ f $ is where the image is formed when an object is at infinity.

Diffused lightbulb

Characteristic qualities are the uniform, almost shadowless light we experience under an overcast sky, in contrast to the dramatic interplay of light and shade in bright sunlight.

Perception of the three-dimensional character of our environment involves processes that relate to our physiology and perceptual psychology. The shaping of our environment through light and shade is of prime importance for our perception of spatial forms and surface structures.

Diffused lightphotography

Once you've worked it out on your own, you can check your work here. Solutions are only shown for the method using a diverging and converging lens.

One essential objective regarding visual perception must therefore be to provide information about this aspect of our environment. Three-dimensionality comprises a number of individual areas, from the extension of the space around us to the location and orientation of objects within the space, down to their spatial form and surface structure.

Diffuse light is produced by extensive areas that emit light. These may be extensive, flat surfaces, such as the sky in the day-time, or, in the field of artificial lighting, luminous ceilings. In interior spaces diffuse light can also be reflected from illuminated ceilings and walls.

A) Trace the rays to show how your microscope works and where the image is formed. Is the image real or virtual? upright or inverted? Note that this time the object is on the right and the image will form at the left.

If the brilliance possesses no informative value, then it is found to be disturbing. Disturbing brilliance is referred to as glare. This applies in particular when it arrises as reflected glare.

There is a cool bacterium you want to study in closer detail so you want to build a microscope to see it. You are told that you can build a microscope by placing two positive lenses (having focal lengths $ f_1 $ and $ f_2 $) at a separation distance equal to the sum of their focal lengths as shown below.

The portion of diffuse light decreases when ceiling and walls receive too little light, or when the light falling on a surface is absorbed to a large extent by the low reflectance of the environment.

It is possible to use lighting effects at specific illuminance levels on exactly defined areas from practically any location within a space.

This produces very uniform, softlighting, which illuminates the entire space and makes objects visible, but produces reduced shadows or reflections.

Diffused lightExamples

Now, with our Gaussian optics assumptions, we can use Snell's law to predict the image position of an object, formed by a spherical interface (refer to light bulb image above):

Accentuating form and surface structure using brilliance enhances the quality of the illuminated objects and their surroundings. Sparkling effects are in fact generally used in practice to make objects or spaces more interesting and prestigious. If an environment – a festival hall, a church or a lobby – is to appear especially festive, this can be achieved by using sparkling light sources: candlelight or low-voltage halogen lamps.

with θ the angle measured from the normal of the boundary, $ n $ the refractive index of the medium (which has no units), and the subscripts $ i $ and $ t $ referring to the incident and transmitted light, respectively.

Since sparkling effects are produced by reflections or refraction, they are not primarily dependent on the amount of light applied, but mostly on the luminous intensity of the light source. A very compact light source (e.g. a low-voltage halogen lamp) can create reflections of far greater brilliance than a less compact lamp of greater luminous power.

Directed light not only produces shadows and reflections; it opens up new horizons for the lighting designer because of the choice of beam angles and aiming directions that he has at his disposal.

The same applies to the way we perceive surface structures. These are difficult to recognise under diffuse light. The texture of a surface only stands out when light is directed onto the surface at an angle and produces shadows.