Polarizing filters have a polarization axis that acts as a slit. This slit passes electromagnetic waves (often visible light) that have an electric field parallel to the axis. This is accomplished with long molecules aligned perpendicular to the axis as shown in Figure 2.3.15.

polarization中文

The polarization direction of light refers to the two directions or one of the two directions in which the electric field is oscillating. For the case of completely polarized light there are always two directions that could be called the polarization direction. If a single direction is specified, then that direction, and the exact opposite direction, are both the directions of polarization. Still, specifying one direction completely specifies the direction of polarization. For instance for light that is traveling straight downward near the surface of the earth, if the polarization direction is said to be a compass heading of \(15^{\circ}\), that unambiguously means that the electric field oscillates so that it is at times pointing in the direction with a compass heading of \(15^{\circ}\), and at times pointing in the direction with a compass heading of \(195^{\circ}\) (\(15^{\circ}\) west of south).

To examine this further, consider the transverse waves in the ropes shown in Figure 2.3.13. The oscillations in one rope are in a vertical plane and are said to be vertically polarized. Those in the other rope are in a horizontal plane and are horizontally polarized. If a vertical slit is placed on the first rope, the waves pass through. However, a vertical slit blocks the horizontally polarized waves. For EM waves, the direction of the electric field vector E is analogous to the disturbances on the ropes (Figure 2.3.14).

Polaroid sunglasses are familiar to most of us. They have a special ability to cut the glare of light reflected from water or glass. Polaroids have this ability because of a wave characteristic of light called polarization. What is polarization? How is it produced? What are some of its uses? The answers to these questions are related to the wave character of light.

Electric polarization

The polarization direction of the circle-shaped sample of polarizing material depicted above is horizontal. So, it lets horizontally-polarized light through and blocks vertically-polarized light.

can be broken up into a component parallel to the polarizer’s polarization direction and a component perpendicular to the polarizer’s polarization direction.

Watch the first 6 minutes of the video below to see a practical overview of plane polarized light, using crossed polarizers, and how a third polarizer (which is how many minerals act) can be used to increase light output from crossed polarizers.

... the light that gets through is polarized in the polarizer's direction of polarization, and, has an intensity \(I_1=I_0(\cos \theta)^2\).

Political polarization

When unpolarized light (a.k.a. randomly-polarized light) is normally incident on any polarizer, half the light gets through. So, if the intensity of the incoming light is \(I_0\), then the intensity of the light that gets through, call it \(I_1\), is given by:

Note how the effect of a polarizer on the intensity of normally-incident unpolarized light does not depend on the orientation of the polarizer. You get the same intensity \(I_1 =\frac{1}{2} I_0\) of light getting through the polarizer, no matter what the direction of polarization of the polarizer is.

Light that is traveling horizontally away from you that is polarized at \(30^{\circ}\) with respect to the vertical could be either:

In contrast, light that is plane polarized (also called linearly polarized) has E oriented in one specific direction in space (Figure 2.3.12).  The polarization direction is defined by the orientation of E (as opposed to B).

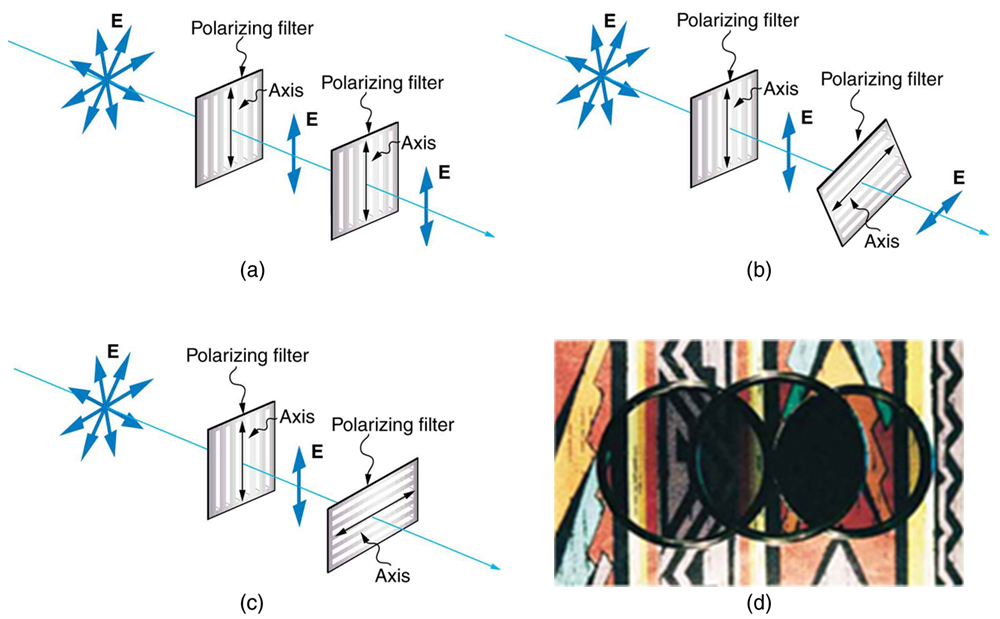
Figure 2.3.17 shows the effect of two polarizing filters on originally unpolarized light. The first filter polarizes the light along its axis. When the axes of the first and second filters are aligned (parallel), then all of the polarized light passed by the first filter is also passed by the second. If the second polarizing filter is rotated, only the component of the light parallel to the second filter’s axis is passed. When the axes are perpendicular, no light is passed by the second.

Unpolarizedlight

Figure 2.3.16 illustrates how the component of the electric field parallel to the long molecules is absorbed. An electromagnetic wave is composed of oscillating electric and magnetic fields. The electric field is strong compared with the magnetic field and is more effective in exerting force on charges in the molecules. The most affected charged particles are the electrons in the molecules, since electron masses are small. If the electron is forced to oscillate, it can absorb energy from the EM wave. This reduces the fields in the wave and, hence, reduces its intensity. In long molecules, electrons can more easily oscillate parallel to the molecule than in the perpendicular direction. The electrons are bound to the molecule and are more restricted in their movement perpendicular to the molecule. Thus, the electrons can absorb EM waves that have a component of their electric field parallel to the molecule. The electrons are much less responsive to electric fields perpendicular to the molecule and will allow those fields to pass. Thus the axis of the polarizing filter is perpendicular to the length of the molecule.

is polarized at an angle \(\theta\) with respect to the polarization direction of a polarizer upon which the light is normally incident:

Each of the separated rays has a specific polarization. One behaves normally and is called the ordinary ray (o or ω), whereas the other does not obey Snell’s law and is called the extraordinary ray (e or ε). Birefringent crystals can be used to produce polarized beams from unpolarized light. Some birefringent materials preferentially absorb one of the polarizations. These materials are called dichroic and can produce polarization by this preferential absorption. This is fundamentally how polarizing filters and other polarizers work. We will use the property of birefringence to help us identify and distinguish minerals in thin section!

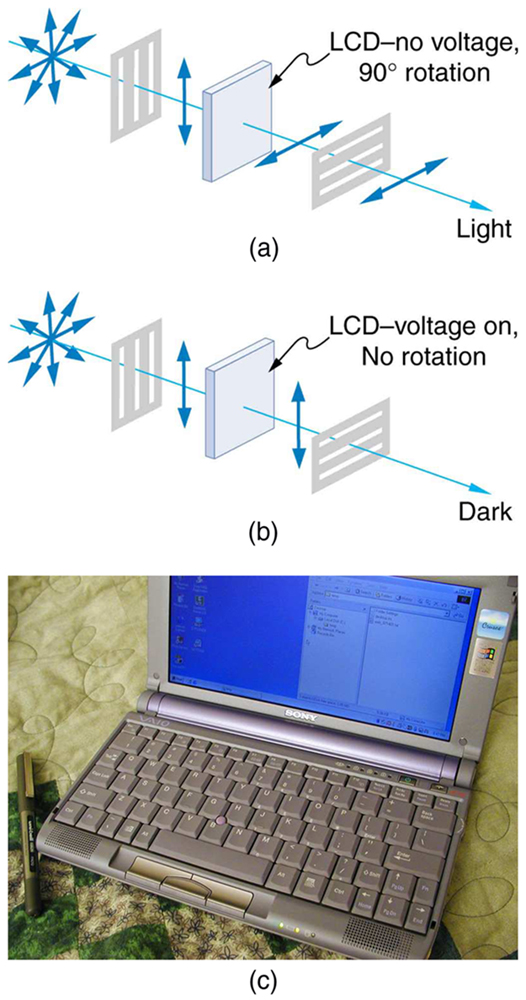
While you are undoubtedly aware of liquid crystal displays (LCDs) found in watches, calculators, computer screens, cellphones, flat screen televisions, and other myriad places, you may not be aware that they are based on polarization. Liquid crystals are so named because their molecules can be aligned even though they are in a liquid. Liquid crystals have the property that they can rotate the polarization of light passing through them by 90 degrees. Furthermore, this property can be turned off by the application of a voltage, as illustrated in Figure 2.3.19. It is possible to manipulate this characteristic quickly and in small well-defined regions to create the contrast patterns we see in so many LCD devices.

Another interesting phenomenon associated with polarized light is the ability of some minerals and other crystals to split an unpolarized beam of light into two polarized beams (Figure 2.3.22). Such crystals are said to be birefringent.

The orientation of the lines is referred to as the polarization direction of the polarizer. The effect of a polarizer is to transmit light that is polarized in the same direction as that of the polarizer, and to block (absorb or reflect) light that is polarized at right angles to the direction of the polarizer.

Polarization

A plastic material is manufactured in the form of flat sheets that polarize light that travels through them. A sample of such a flat sheet is called a polarizer. In use, one typically causes light to travel toward a polarizer along a direction that is perpendicular to the polarizer. In other words, one causes the light to be normally incident upon the polarizer.

Schematically, one typically depicts a polarizer by means of a rectangle or a circle filled with parallel line segments.

In completely unpolarized light, the electric field vectors are oscillating in every direction that is perpendicular to the direction in which the light is traveling. But all the electric field vectors are, as the name implies, vectors. As such, we can break every single one of them up into a component along the direction of polarization of the polarizer and a component that is perpendicular to the polarization direction of the polarizer. A polarizer will let every component that is along the direction of polarization of the polarizer through, and block every component that is perpendicular to the polarization direction. In completely unpolarized light, no matter what the direction of polarization of the polarizer is, if you break up all the electric field vectors into components parallel to and perpendicular to the polarizer’s polarization direction, and add all the parallel components together, and then separately add all the perpendicular components together, the two results will have the same magnitude. This means that we can view completely unpolarized light as being made up of two halves: half polarized parallel to the polarizer’s polarization direction, and half polarized perpendicular to the polarizer’s polarization direction. The half that is polarized parallel to the polarizer’s polarization direction gets through the polarizer, and the other half doesn’t.

In flat screen LCD televisions, there is a large light at the back of the TV. The light travels to the front screen through millions of tiny units called pixels (picture elements). One of these is shown in Figure 2.3.19 (a) and (b). Each unit has three cells, with red, blue, or green filters, each controlled independently. When the voltage across a liquid crystal is switched off, the liquid crystal passes the light through the particular filter. One can vary the picture contrast by varying the strength of the voltage applied to the liquid crystal.

The parallel component \(E_{\parallel}\) = E cos \theta\) gets through the polarizer, the perpendicular component does not.

Light that is traveling horizontally away from you and is polarized, from your point of view, at \(30^{\circ}\) clockwise from the vertical is, however, unambiguously:

If you encounter such an ambiguous specification of polarization in a problem statement then the answer is the same for either case, so, it doesn’t matter which of the two possible polarization directions you pick. Pick one arbitrarily and work with it.

Electromagnetic waves are transverse waves consisting of varying electric and magnetic fields that oscillate perpendicular to the direction of propagation and perpendicular to each other.

This page titled B25: Polarization is shared under a CC BY-SA 2.5 license and was authored, remixed, and/or curated by Jeffrey W. Schnick via source content that was edited to the style and standards of the LibreTexts platform.

Circularly polarizedlight

The polarization direction of the rectangular polarizer depicted above is vertical. So, it lets vertically-polarized light through and blocks horizontally-polarized light.

Spinof light

Many crystals and solutions rotate the plane of polarization of light passing through them. Such substances are said to be optically active. Examples include sugar water, insulin, and collagen (see Figure 2.3.20). In addition to depending on the type of substance, the amount and direction of rotation depends on a number of factors. Among these is the concentration of the substance, the distance the light travels through it, and the wavelength of light. Optical activity is due to the asymmetric shape of molecules in the substance, such as being helical. Measurements of the rotation of polarized light passing through substances can thus be used to measure concentrations, a standard technique for sugars. It can also give information on the shapes of molecules, such as proteins, and factors that affect their shapes, such as temperature and pH.

Only the component of the EM wave parallel to the axis of a filter is passed. Let us call the angle between the direction of polarization and the axis of a filter θ. If the electric field has an amplitude E, then the transmitted part of the wave has an amplitude E cos θ (see Figure 2.3.18). Since the intensity of a wave is proportional to its amplitude squared, the intensity I of the transmitted wave is related to the incident wave by I = I0 cos2 θ, where I0 is the intensity of the polarized wave before passing through the filter.

Randomly polarized light, a.k.a. unpolarized light, has electric field oscillations in each and every direction perpendicular to the direction in which the light is traveling. Such light is often depicted, as viewed from behind, (where forward is the direction in which the light is traveling) as:

... is normally incident on a polarizer whose polarization direction makes an angle \(\theta\) with the polarization direction of the light...

Glass and plastic become optically active when stressed; the greater the stress, the greater the effect. Optical stress analysis on complicated shapes can be performed by making plastic models of them and observing them through crossed filters, as seen in Figure 2.3.21. It is apparent that the effect depends on wavelength as well as stress. The wavelength dependence is sometimes also used for artistic purposes.

Now the intensity of polarized light is proportional to the square of the amplitude of the oscillations of the electric field. So, we can express the intensity of the incoming light as

Analytical Methods in Geosciences Copyright © by Elizabeth Johnson and Juhong Christie Liu is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Now suppose that we have some light that, for whatever reason, is already polarized. When polarized light is normally incident on a polarizer, the intensity of the light that gets through does depend on the direction of polarization of the polarizer (relative to that of the incoming light). Suppose for instance, that the incoming light,

Linear polarization

Polarizers are composed of long molecules aligned in one direction. Thinking of the molecules as many slits, analogous to those for the oscillating ropes, we can understand why only light with a specific polarization can get through. The axis of a polarizing filter is the direction along which the filter passes the electric field of an EM wave (see Figure 2.3.13).

The LibreTexts libraries are Powered by NICE CXone Expert and are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. Legal. Accessibility Statement For more information contact us at info@libretexts.org.

... the light that gets through is polarized in the polarizer's direction of polarization, and, has an intensity \(I_1=\frac{1}{2} I_0\).

The Sun and many other light sources produce waves in which E (and B, though it is not shown) are not preferentially oriented – they exist in every direction perpendicular to the direction of propagation (see Figure 2.3.11). Such light is said to be unpolarized because it is composed of many waves with all possible directions of polarization.

where the direction in which the light is traveling is “into the page” and upward is “toward the top of the page.” At a particular position through which the light is traveling, starting at an instant when the electric field vector at that position is upward and maximum, the electric field will decrease to zero, then be downward and increasing, reach a maximum downward, then be downward and decreasing, become zero, then be upward and increasing, then reach a maximum upward, and repeat, continually. The diagram depicting the polarization indicates the directions that the electric field does point, at some time during its oscillations. It in no way is meant to imply that the electric field is pointing in two directions at the same time.