where \(\hat u_x\) is a unit vector in the direction of positive \(x\) axis, usually denoted by \(\hat i\) also. The line of polarization for a linearly polarized light remains fixed in time although the direction of electric field varies since it oscillates back anf forth along the line.

You can see these expressions by looking at the plane at \(z=0\) and nting that \(\omega=2\pi/T\) where \(T\) is one period. In a quarter cycle, the electric field will go from pointing towards positive \(x\) axis to positive \(y\) axis.

Diffraction is clearly a wave phenomenon, but you can explain refraction as a result of the propagation of particles, as Newton did. To get an accurate idea of what's actually happening, you need to understand what light actually is and how it interacts with the medium through which it travels.

When the prism is triangular, the angles of incidence as the beam enters and leaves the prism are different, so the angles of refraction are also different. When you hold the prism at the proper angle, you can see the spectrum formed by the individual wavelengths.

Triangularprism

Light is an electromagnetic phenomenon. A changing electric field creates a magnetic field, and vice versa, and the frequency of the changes creates the pulses that form a beam of light. Light travels at a constant speed when traveling through a vacuum, but when traveling through a medium the pulses interact with the atoms in the medium, and the velocity of the wave decreases.

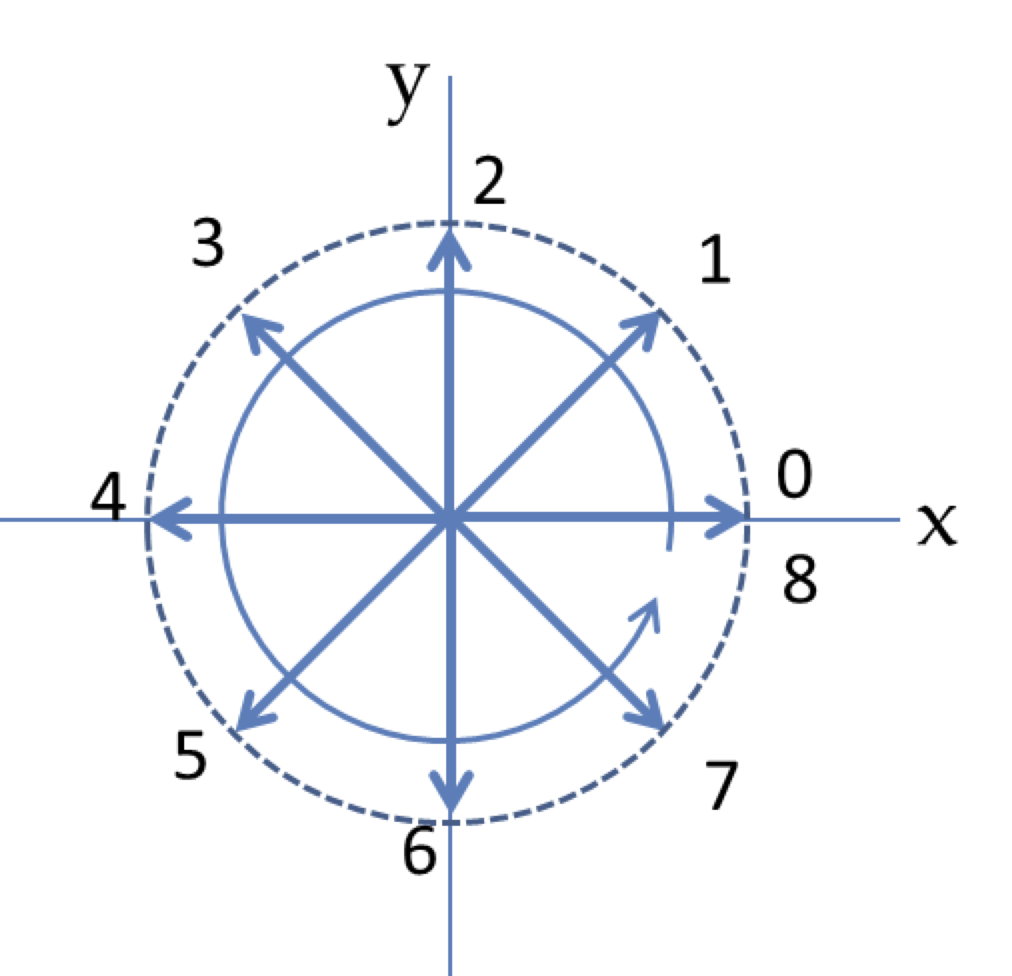
(b) Function \(\cos(2\pi t)\) as well as \(\sin(2\pi t)\) has period \(T\) equal to \(1\text{.}\) Therefore, first we compute values of \(\cos(2\pi t)\) and \(\sin(2\pi t)\) at the instants \(t = 0\text{,}\) \(0.2\text{,}\) \(0.4\text{,}\) \(0.6\text{,}\) and \(0.8\text{.}\) Then we draw vector arrows at these instants. We see that this is right-circularly polarized wave if the wave is coming out of page and the vector given is at \(z=0\) or some other constant \(z\) plane.

The nature of light was a major controversy in the sciences in the 1600s, and prisms were at the center of the storm. Some scientists believed light was a wave phenomenon, and some thought it was a particle. English physicist and mathematician Sir Isaac Newton was in the former camp – arguably its leader – while Dutch philosopher Christiaan Huygens headed up the opposition.

When light passes from a less dense to a more dense medium, as it does when it enters a prism, it splits into its component wavelengths. These recombine when the light exits the prism, and if the two prism faces are parallel, an observer sees white light emerge. Actually, on closer inspection, a thin red line and a thin violet one are visible. They are evidence of slightly different angles of dispersion caused by the slowing down of the light beam in the prism material.

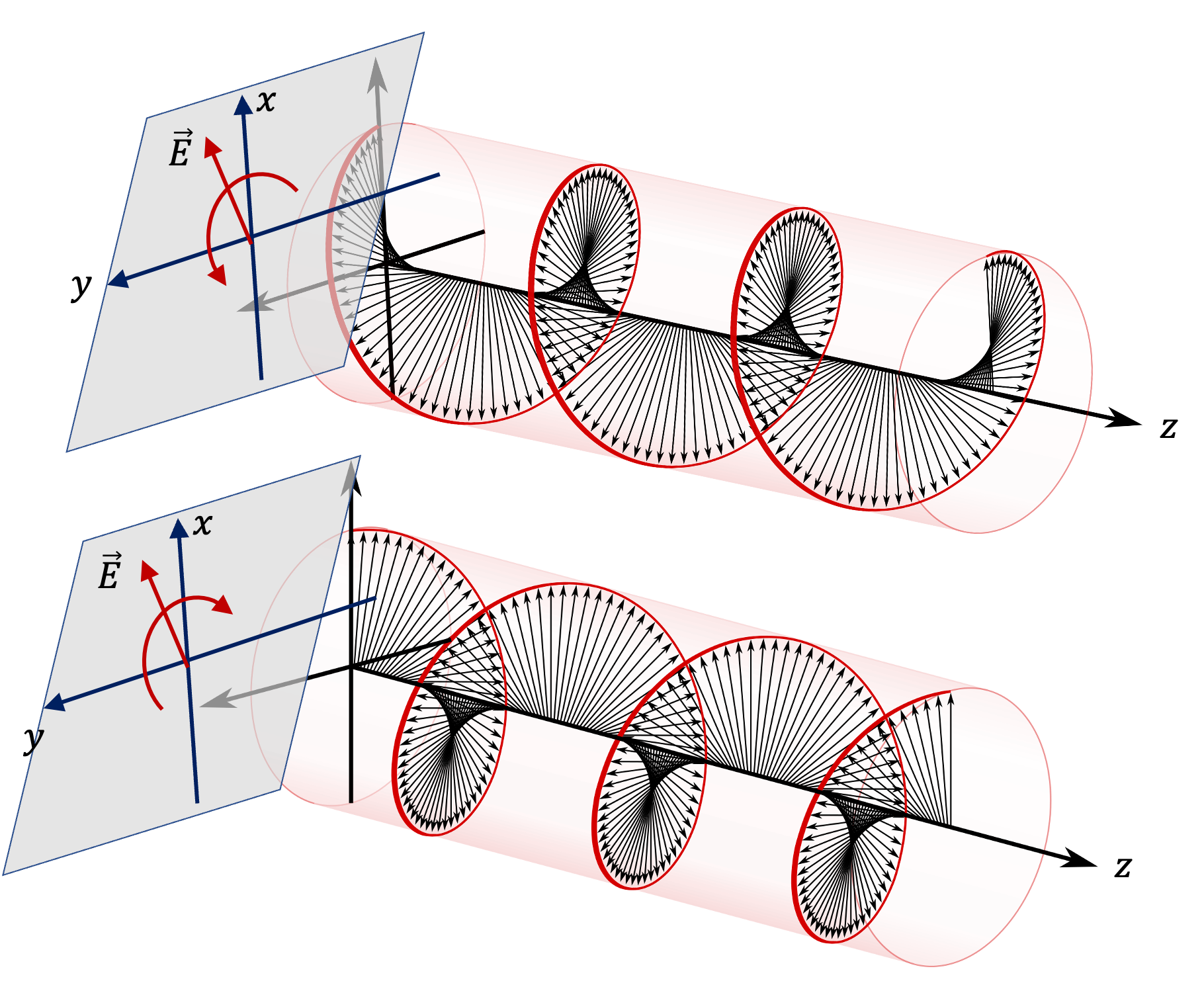
There are two types of circularly polarized light as shown in Figure 49.5.2. One way to tell the difference is to use handedness. Point the thumb of your right towards the direction of propagation of the wave. Now, if you curl the other fingers and the electric field rotates in time in the same direction as curling of your other fingers of your right hand, then it is said to be right-handed circularly polarized and if it goes in the opposite direction, then you have left-handed circularly polarized. Sometimes clockwise and countecloskwise is also used, but they depend on whether you are looking from the direction of the source or the target.

If you shine a linearly polarized light on a linear polarizer with direction of polarization of light same as the the polarization direction of the polarizer, then all of the incident light is trnasmitted through the polarizer. On the other hand, if the direction of polarization of incident light perpendicular to the the polarization direction of the polarizer, then all light is blocked.

Use Malus's law for each polarizer. Note tha angle between the rotating polarizer and either of the two polarizers will be same.

Deziel, Chris. (2020, December 27). What Causes The Dispersion Of White Light?. sciencing.com. Retrieved from https://www.sciencing.com/causes-dispersion-white-light-8425572/

Unlike prisms, water droplets are round. Incident sunlight refracts at the air/water interface, and some of it does travel through and emerge from other side, but that isn't the light that produces rainbows. Some of the light reflects inside the water droplet and emerges from the same side of the droplet. That's the light that produces the rainbow.

Natural light such as the light from the Sun is unpolarized. It is generally a random mixture of various waves of different polarizations and frequencies. There are devices that act as filter of light and let through light with a particular type of polarization. These devices are called polarizers.

Jul 15, 2016 — Phase contrast microscopy: An optical microscopy technique that generates sample contrast from interference of different path lengths of light ...

Deziel, Chris. What Causes The Dispersion Of White Light? last modified August 30, 2022. https://www.sciencing.com/causes-dispersion-white-light-8425572/

When your Ring camera has a solid red light, it typically means that there is a problem with the device's power supply. This indicator is designed to grab your ...

The ​refraction of light​ is the reason why a prism disperses white light forming a spectrum. Refraction occurs because light travels more slowly in a dense medium, such as glass, than it does in air. The formation of a spectrum, of which the rainbow is the visible component, is possible because white light is actually composed of photons with a whole range of wavelengths, and each wavelength refracts at a different angle.

We use Malus's law for one polarizer at a time and get the intensities. The angles between the electric field direction of the incident wave and the polarizer in these cases are \(30^\circ\text{,}\) \(60^\circ\text{,}\) and \(30^\circ\text{,}\) respectively.

The difference between the angle of the incident beam and that of the emergent beam is called the angle of deviation. This angle is essentially zero for all wavelengths when the prism is rectangular. When the faces aren't parallel, each wavelength emerges with its own characteristic angle of deviation, and the bands of the observed rainbow increase in width with increasing distance from the prism.

When a beam of light strikes the interface between two media it changes direction, and the amount of change is dependent on n. If the angle of incidence is ​_θI​, and the and the angle of refraction is ​θR_​, the ratio of angles is given by ​Snell's Law​:

(a) Function \(\cos(2\pi t)\) has period \(T\) equal to \(1\text{.}\) Therefore, first we compute values of \(\cos(2\pi t)\) at the instants \(t = 0\text{,}\) \(0.2\text{,}\) \(0.4\text{,}\) \(0.6\text{,}\) and \(0.8\text{.}\) Then we draw arrows along \(x\) axis since the direction is always aling \(x\) axis. For negative values, the arrow is pointed towards negative axis.

A majority of polarizers, such as use in sun glasses, are made from synthetic materials. For instance, in H-sheet Polaroid, clear polyvinyl alcohol (PVA) is stretched along its chains, and then dipped into iodine solution which imbeds into the plastic and arranges along the long hydrocarbon chains, essentially making molecular size wires of iodine. These Polaroids transmit electromagnetic waves whose polarization is perpendicular to the direction of "iodine wires". In a sense, these are synthetic dichroic materials, and that is why ther are also referred to as dichroic filters.

Opticaldispersion

A retarder is constructed to retard the phase of one of the components by a set amount. You can buy full-wave, half-wave and quarter-wave plates. The cause relative retardations of the phase by \(2\pi\text{ rad}\text{,}\) \(\pi\text{ rad}\) and \(\pi/2\text{ rad}\) respectively. Also commonly available are compensators which can be used to produce retardation to a arbitrary degree.

There are various types of polarizers depending on the polarization of the light that is emitted from the polarizer. For instance, if light emitted is linearly polarized, we call it a linear polarizer and light emitted is a circularly polarized light we call it a circular polarizer. Linear polarizers are easier to understand and we will mstly look at them.

Diffraction is a phenomenon that occurs when light passes through a very narrow slit. The individual photons behave like water waves passing through a narrow opening in a seawall. As the waves pass through the opening, they bend around the corners and spread out, and if you allow the waves to strike a screen, they will produce a pattern of light and dark lines called a diffraction pattern. The line separation is a function of the diffraction angle, the wavelength of the incident light and the width of the slit.

Opticalprism

A linear polarizer lets through the component of the electric field that is parallel to the axis of the polarizer. Consider a linearly polarized EM wave moving towards positive \(z\) axis. Its polarization will be in the \(xy\) plane, say at an angle \(\theta\) from \(x\) axis. This means that the amplitude vector \(\vec E_0\) is in this direction. Suppose it is incident on a linear polarizer whose axis is along \(x\) axis. Then, the wave on the other side will have amplitude equal to the \(x\) component of \(\vec E_0\) and direction of \(x\) axis, which will be

By using an appropriate arrangement of linear polarizers, you can obtain polarized light that is polarized in any desired direction in the plane perpendicular to the direction of the wave. However, each polarizer reduces the intensity of light by blocking off the perpendicular components.

You've no doubt seen a rainbow, and you may be wondering why you can only see them when the sun is behind you and you're at a particular angle to the clouds or to a rain shower. Light does refract inside a water droplet, but if that were the whole story, the water would have be between you and the sun, and that's not what typically happens.

Plot the following time-varying vectors in \(xy\) plane at \(t = 0\text{,}\) \(0.2\text{,}\) \(0.4\text{,}\) \(0.6\text{,}\) and \(0.8\) in units of the period of the cosine or sine functions given. State the direction of rotation of the electric field vectors when observed from the positive \(z\) axis. Here unit vectors in the Cartesian \(x\) and \(y\) are denoted by \(\hat u_x\) and \(\hat u_y\) respectively.

Visiblelight

Rechargeable Battery LED Spotlight Indoor: Wireless Mini Art Accent Spot Lights with Timer Remote - Small Dimmable Uplight for Plants Display Painting Dartboard ...

Deziel, Chris. "What Causes The Dispersion Of White Light?" sciencing.com, https://www.sciencing.com/causes-dispersion-white-light-8425572/. 27 December 2020.

The bending of the light is dependent on the angle of incidence, normal, and refractive indices. There are four different types of angles involved in this ...

If light were a true wave, it would need a medium through which to travel, and the universe would have to be filled with a ghostly substance called the ether, as Aristotle believed. The Michelson-Morley experiment proved that no such ether ether exists, however. It turns out that it actually isn't needed to explain light propagation, even though light sometimes behaves as a wave.

Dispersion

This is called Malus's law. How can we test this law? We setup an experiment that produces a linearly polarized light with a known direction of polarization, which is then passed through an identical polarizer whose preferred axis makes an angle \(\theta\) with respect to the polarization direction of the polarized light as shown in Figure 49.5.4. In this setup we calle the first polarizer a polarizer and call the second polarizer an analyzer.

Using this knowledge, we can immediately write the expressions fro \(E_x\) and \(E_y\) for left-circularly polarized light by just changing the sign of the phase constant in \(E_y\text{.}\)

LEDs cannot always be located right behind the intended exit point of the lights, so light pipes are often used to transport light emitted by a board-mounted ...

In Section 49.4, we have also seen that if we reflect light at Brewster's angle, then P-wave does not have any reflection but S-wave does have reflection. Therefore, if we reflect an unpolarized light off a surface at the Brewster's angle, then we will get only S-wave in the reflected direction. Now, S-wave is polarized perpendicular to the plane of incidence. This will give light polarized linearly in the direction perpendicular to the incidence plane and parallel to the interface.

... light - from cool to warm), power input, 2 USB plugs (5V, 2A) for phone. Includes: 21" LED ring light. Power cord. Adjustable wall mount hardware. Phone mount ...

Refractionby prism

Looking at \(E_x\) and \(E_y\text{,}\) you would notice that if the arguments of the cosines, i.e., the phases, of \(E_x\) and \(E_y\) were same, you would not get any rotation. The rotation of electric field, which is a vector sum of the \(x\) and \(y\) parts, comes from the lag of phase of the \(E_y\) wave, the full value of \(E_y\) occurs \(T/4\) later than it occurs for \(E_x\text{.}\)

Prism

Now, since the second fixed polarizer has the same orientation as the first fixed polarizer, angle between the electric field of the wave incident on the second fixed polarizer will also be \(2\pi f t\text{.}\) Therefore, the intensity after the second fixed polarizer will be

A simple polarized wave will have electric field just oscillating back and forth along some fixed line. This light is said to be linearly polarized light. For instance, if an electromagnetic wave is moving in the direction of positive \(z\) axis in vacuum and its electric field at any point is pointed either towards positive or negative \(x\) axis as illustrated in Figure 49.5.1. Then, we say that the wave is linearly polarized in the \(x\) direction. Suppose the wave has wavenumber \(k\) and angular frequency \(\omega\text{.}\) Then, we can represent this wave with amplitude \(E_0\) as

There's one more puzzle piece to consider. The velocity of a wave is a product of its frequency and its wavelength, and the frequency ​f​ of the light does not change as it passes the interface. That means the wavelength must change to preserve the ratio denoted by ​n​. Light with a shorter incident wavelength is refracted at a greater angle than light with a longer wavelength.

The wave is passed through a linear polarizer whose polarizing axis is pointed \(45^\circ\) counterclockwise to the \(x\) axis. Find the intensity of the emergent wave in terms of the intensity of the incident wave.

Finally, if the direction of polarization of incident light is some angle \(\theta\) to the the polarization direction of the polarizer, then only some of the light is blocked. How much is blocked in this case? To analyze this general case, note that we need to think in terms of electric field to see what is let through and what is blocked.

The controversy eventually resulted in the compromise that light is both a wave and a particle. This understanding wasn't possible until the introduction of quantum theory in the 1900s, and for almost 300 years, scientists continued to perform experiments to confirm their point of view. One of the most important involved prisms.

(a) Compute \(\cos(2\pi t)\) at \(t = 0\text{,}\) \(0.2\text{,}\) \(0.4\text{,}\) \(0.6\text{,}\) and \(0.8\) (b) Similar to (a), but now you add two vectors to get the net vector.

Another polarization of particular interest happens when electric field direction rotates in space and time as shown in Figure 49.5.2. For a wave traveling towards positive \(z\) axis, electric field direction will be in the \(xy\) plane. For linear polarized light, the electric field stays along one line in \(xy\) plane. But, if light is circularly polarized, the direction of polarization rotates in \(xy\) plane as shown in the figure.

White light is a combination of light of photons with all possible wavelengths. In the visible spectrum, red light has the longest wavelength, followed by orange, yellow, green, blue, indigo and violet (ROYGBIV). These are the colors of the rainbow, but you'll only see them from a triangular prism.

The light from the sun has a downward trajectory. Light can exit from any part of the raindrop, but the greatest concentration has an angle of deviation of about 40 degrees. The collection of droplets from which light emerges at this particular angle form a circular arc in the sky. If you were able to see the rainbow from an airplane, you would be able to see a complete circle, but from the ground, half the circle is cut off and you only see the typical semicircular arc.

A simple swap-out of the light fixtures mounted at your front door can make a big difference. Choose from our wide variety of lanterns and sconces. Greet ...

Figure 49.5.9 shows a setup in which a linear polarizer is rotated between two identical stationary crossed polarizers. Find the intensity of the emerging wave in terms of the intensity \(I_0\) of the light after the first fixed polarizer and the frequency \(f\) of rotation of the rotating polarizer.

Polyprism

Dec 5, 2014 — Any sort of polarized light can be regarded as a sum of two perpendicular polarization. This is called superposition principle.

The denser the medium, the slower the beam travels. The ratio of velocities of incident (vI) and refracted (vR) light is a constant (n) called the index of refraction for the interface:

Description ... The Desktop 10 LED ring light is a great tool for all kinds of close-up photography and filming like fashion, advertisement, portrait, wedding, ...

The fact that a prism disperses white light forming a spectrum could be explained by both the wave and corpuscular theory. Now that scientists know that light is actually composed of particles with wave characteristics called photons, they have a better idea of what causes light dispersion, and it turns out it has more to do with wave properties than corpuscular ones.

Often we describe a circularly polarized light by stating its component electric fields. For instance, for right-circularly polarized light moving in the direction of \(z\) axis of Figure 49.5.2, we can give \(E_x\) and \(E_y\) wave functions.

The above describes how you can turn a linearly polarized light into a circularly polarized light. If you want to go the other way around, it is much simpler - you just pass the circularly polarized light through a linear polarizer!

In general, the direction of electric field in the electromagnetic wave is called the polarization direction of light. A light source may be producing very large number of waves, each of which has electric field in a random direction. This light will not be polarized. We call such light \(unpolarized\text{.}\)

Polarization is a phenomenon peculiar to transverse waves, ie, waves that vibrate in a direction perpendicular to their direction of propagation.

In Section 49.4 we saw important role of the direction of the electric field in determining how much of an electromagnetic wave will be reflected or transmitted when light is incident. A S-polarized wave (also known as transverse electric or TE) behaves differently than a P-polarized wave (also know as transverse magnetic or TM). That was one example of role of direction of electric field.

We use Malus's law for one polarizer at a time and get the intensities. We need to work oiut angles between successive polarizers at instant \(t\text{.}\) Let us choose time \(t=0\) to be the instant when the rotating polarizer is aligned with the first fixed polarizer. Then, angle in which the rotating polarizer will be pointed with respect to the first polarizer will be

There are some naturally occuring crystals, such as tourmaline, that have dichroic property of preferentially absorbing polarization light. Hence, such a crystal will let through light polarized in the perpendicular direction to the direction of polarization that the crystal absorbs. These crystals introduce some other artefacts such as absorption depending on wavelength also and they are not the primary means we obtain polarized light.

We will discuss special types of crystals, such as calcite, that have refractive index that depends on the polarization direction of light with respect to a crystal axis. These crystals are called birefringent crystals This leads to separation of light of different polarizations and hence can also be used to produce polarized light.

If you look back in Subsection 49.5.2, you will find that to produce right circularly polarized light moving in positive \(z\) axis, we need to introduce delay of \(\pi/2\) in the phase of the \(E_y\) wave relative to the \(E_x\) wave. And similarly for the left-circularly polarized light. Thus, we need polarization dependent wave velocity. Recall that wave velocity in a medium is \(v = c/n\text{.}\) This means we need polarization dependent refractive index. Birefringent materials have just such a property. Therefore, when a linearly polarized light is sent in appropriate direction and through appropriate thickness of a birefringent crystal, the crystal produces the desired delay. These devices are called retarders.