We have been investing heavily in platform development across the C> and Chemistry, Manufacturing, and Control (CMC) spaces.

At Porton Advanced Solutions, we are committed to accelerating delivery of life-changing advanced therapies to patients. As a C> CRO and CDMO company, we provide end-to-end biopharma solutions and services to our clients throughout the development and commercialization of their therapeutics

Light intensityto electric field

Traveling waves transport energy from one place to another without actually moving particles. Therefore, you can think of an electromagnetic wave in terms of the flow of the electromagnetic energy.

(a) Use \(\lambda f = c\text{.}\) (b) Use \(I= \frac{1}{2}c\epsilon_0 E_0^2\text{.}\) (c) Recall for spherically symmetric waves \(I\sim 1/r^2\text{.}\)

Light intensityunit

A spherical wave from a point source at the origin has an electric field that drops with the radial distance $r$ from the origin as follows.

Our dedicated process and analytical development teams have built up proprietary technologies for client’s licenses and robust platform-based USP/DSP tailored to client’s manufacturing needs.

Consider an electromagnetic wave in vacuum. The energy per unit volume contained in the oscilalting electric and magnetic fields, or energy density, to be denoted by small letter \(u\text{,}\) is sum of energy in the electric field and energy in the magnetic field. From your studies of electromagnetism, you would be able to write it as

If the wave is not in vacuum but in some other linear medium such as glass or air we will need to replace the speed \(c\) by the speed \(v\) in the medium, the permittivity \(\epsilon_0\) by \(\epsilon\text{,}\) and the permeability \(\mu_0\) by \(\mu\text{.}\)

luminous intensity中文

Our goal is to improve availability and commercial viability of these life-changing treatments by accelerating therapeutic development through our unique, innovative approach.

For a plane electromagnetic wave, we plug in the expressions for electric and magnetic waves given above and obtain the following for energy per unit volume.

Our innovative, integrated approach enables us to respond to the full needs of each individual customer. We provide end-to-end biopharma solutions according to each client’s needs across multiple therapeutic platforms.

Light intensityformula

Figure 49.2.3 shows a source of light, such as sun, at the center and two spherical surfaces in space at radii \(r_1\) and \(r_2\text{.}\) Let the intensities at \(r_1\) and \(r_2\) be denoted by \(I_1\) and \(I_2\) respectively.

Our clients include a wide range of biotech and pharmaceutical companies, academic research institutes, and hospitals, each with unique needs spanning across discovery research, drug development, different clinical phases, and commercialization.

Our services include gene and cell engineering discovery research and technology licensing, process development and analytical development, testing, drug substances (DS) and drug products (DP), and cGMP manufacturing across plasmids, cell engineering, gene therapy, virotherapy, and mRNA-based therapeutic platforms.

In Figure 49.2.2, notice that some of the rays passign through \(A_1\) will not pass through area \(A_2\) even though the two surfaces are equal in value. This is due to mismatch of the perpendicular to the area direction and the direction of the wave. It is easy to incorporate this if we use vector notation for the area.

where \(V_0 = 10\text{ V}\text{,}\) \(f = 2 \times 10^{14}\text{ Hz}\text{,}\) and \(k\) is the wave number. Assume speed of light to be equal to the speed of light in vacuum.

Opticalintensity

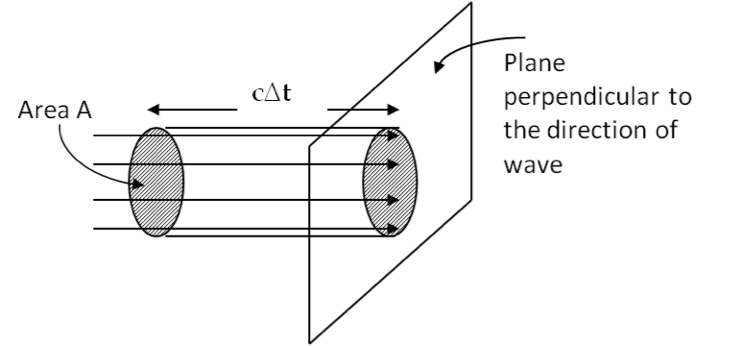
Now, we look at how much energy is the wave transporting in unit time. We will use the setup given in Figure 49.2.1. Since the \(u\) wave is moving at the same speed \(c\) as the EM wave, the energy contained in the volume \(Ac\Delta t\) will pass through area \(A\) in time \(\Delta t\text{.}\) That is,

If we know how much power is flowing on average over, \(P_\text{av}\) some area of cross-section A, then this definition gives us intensity immediately.

The vector product of \(\vec E\) and \(\vec B\) makes it evident that the Poynting vector \(\vec S\) points in the direction of the propagation of the electromagnetic wave. Now, that takes care of the direction of the energy wave. Now, to take care of the orientation of the area, we introduce an area vector of a plane by its magnitude equal to the area and its direction perpendicular to the surface. Let \(A\) be the magnitude of the area and \(\hat n\) a unit vector in the perpendicular direction. Then, define area vector as

Eq. (49.2.7) can also be used to relate intensity to electric field and magnetic field. Note that time-averaging of the expression for the power flux given in Eq. (49.2.6) is easily performed by noting that it has a constant part and a part that fluctuates between \(-1\) and \(1\text{.}\) The avergage of the fluctuating part over any integral multiple of cycles will be zero. Therefore, time average over long times will give a zero for the fluctuating part.

(c) For spherical waves, \(I\) will drop off as square of distance. Therefore, we can get intensity at \(2\text{ cm}\) by simply using the value in (b).

To cover an arbitrary surface with flat patches, we will need infintely many patches, each of infinitesimal area. This gives the following general formula for power crossing any arbitrary surface.

Luminousintensity

Porton Advanced Solutions is a subsidiary of the leading CDMO Porton Pharma Solutions. Porton Pharma Solutions is globally recognized and trusted for its process innovation, supply chain performance and compliance with global quality and EHS standards.

Actually, there are two normal directions to a flat area. Here, we choose it arbitrarily. Then energy crossing an area vector \(\vec A\) per unit time will be

Since energy passing the spherical surface with radius \(r_1\) in an interval \(\Delta t\) must equal the energy passing through the surface with radius \(r_2\) in the same interval of time. Multiplying intensity with area and time gives energy. Therefore

Consider a point source that emits light in a spherical symmetric way. The conservation of energy can be used to show that intensity must drop off from the source as inverse square of distance.

How islight intensitymeasured

lightintensity中文

6 Cedarbrook Drive, Cranbury, NJ 08512 (USA) • +1 (908)-565-4183 • info@portonadvanced.com • linkedin.com/company/porton-advanced

Since the frequency of the visible light is very high (of the order of \(10^{14}\) cycles per second) the power flux will be an extremely rapidly varying quantity. Our eyes as well as most light energy measuring instruments cannot respond this fast and only an average energy over many cycles is observed. The quantity obtained by time-averaging the power flux is called the intensity or irradiance and it is normally denoted by \(I\text{.}\)

If surface is not flat but some other surface, we can divide the surface into smaller patches and define area vectors in each “flat” patch. Then on each patch, \(\Delta \vec A\text{,}\) we will get

Dividing Eq. (49.2.3) by \(A\Delta t\text{,}\) will give us power flow per unit corss-sectional area. This is called power flux and denoted by \(S\text{.}\) Using various equations above, we can express it as