9.2 - Diffuse Lighting — LearnWebGL - diffused light meaning

 2024-08-08 13:27:00

Confocalmicroscopy

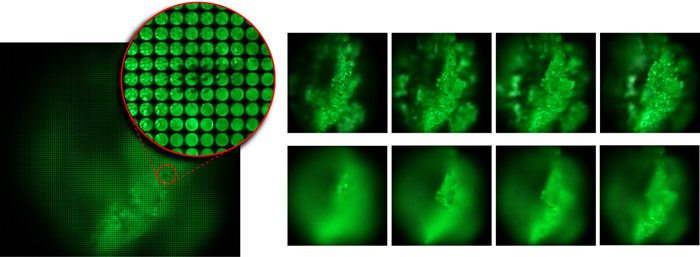
Note: In the printed proceedings, figure 1 came out poorly. Please refer instead to the version in the PDF file (also reproduced above).

Optical microscope

Vector notation: where and are 3-vectors, with . Here central projection is represented in the coordinate frame attached to the camera. Generally, there is not direct access to this camera coordinate frame. Instead, we need to determine the mapping from a world coordinate frame to an image coordinate system (see next slide). Bob Fisher Wed Apr 16 00:58:54 BST 1997

Phase contrastmicroscopy

Optical recipes for light field microscopes non-infinity optics, see memo for caption In our SIGGRAPH paper, figure 2 gives the optical layout of our prototype light field microscope. Unfortunately, this figure and its accompanying caption do not provide quite enough detail to set up and adjust a light field microscope. This brief technical memo provides a more detailed optical layout, with emphasis on how to vertically position and focus each element in the optical train. We show this first for microscopes having non-infinity-corrected optics (as in our SIGGRAPH paper). We then describe an arrangement suitable for microscopes employing infinity-corrected optics, which is the more common case. Finally, we address the often-asked question of whether our microscope light fields contain aliasing. (Yes they do.) infinity optics © Copyright 2006 by Marc Levoy Last update: June 6, 2010 06:34:32 PM

where and are 3-vectors, with . Here central projection is represented in the coordinate frame attached to the camera. Generally, there is not direct access to this camera coordinate frame. Instead, we need to determine the mapping from a world coordinate frame to an image coordinate system (see next slide). Bob Fisher Wed Apr 16 00:58:54 BST 1997

Marc Levoy Ren Ng Andrew Adams Matthew Footer Mark Horowitz Stanford University ACM Transactions on Graphics 25(3), Proceedings of SIGGRAPH 2006 Abstract: By inserting a microlens array into the optical train of a conventional microscope, one can capture light fields of biological specimens in a single photograph. Although diffraction places a limit on the product of spatial and angular resolution in these light fields, we can nevertheless produce useful perspective views and focal stacks from them. Since microscopes are inherently orthographic devices, perspective views represent a new way to look at microscopic specimens. The ability to create focal stacks from a single photograph allows moving or light-sensitive specimens to be recorded. Applying 3D deconvolution to these focal stacks, we can produce a set of cross sections, which can be visualized using volume rendering. In this paper, we demonstrate a prototype light field microscope (LFM), analyze its optical performance, and show perspective views, focal stacks, and reconstructed volumes for a variety of biological specimens. We also show that synthetic focusing followed by 3D deconvolution is equivalent to applying limited-angle tomography directly to the 4D light field. Information available: The paper (PDF file) 4-minute video (.mov file, MPEG-4, 22 MB) The Powerpoint slides from my presentation at SIGGRAPH 2006. Our project web page, which includes links to more results and movies. LFDisplay: a software package for real-time viewing of microscope light fields. The package includes sample light fields and step-by-step instructions on how to build a Light Field Microscope (LFM). A web page describing other devices we have built to capture light fields. Note: In the printed proceedings, figure 1 came out poorly. Please refer instead to the version in the PDF file (also reproduced above). Optical recipes for light field microscopes non-infinity optics, see memo for caption In our SIGGRAPH paper, figure 2 gives the optical layout of our prototype light field microscope. Unfortunately, this figure and its accompanying caption do not provide quite enough detail to set up and adjust a light field microscope. This brief technical memo provides a more detailed optical layout, with emphasis on how to vertically position and focus each element in the optical train. We show this first for microscopes having non-infinity-corrected optics (as in our SIGGRAPH paper). We then describe an arrangement suitable for microscopes employing infinity-corrected optics, which is the more common case. Finally, we address the often-asked question of whether our microscope light fields contain aliasing. (Yes they do.) infinity optics © Copyright 2006 by Marc Levoy Last update: June 6, 2010 06:34:32 PM

Darkfield microscopy

Note: In the printed proceedings, figure 1 came out poorly. Please refer instead to the version in the PDF file (also reproduced above).

Differential interference contrastmicroscopy

Here central projection is represented in the coordinate frame attached to the camera. Generally, there is not direct access to this camera coordinate frame. Instead, we need to determine the mapping from a world coordinate frame to an image coordinate system (see next slide). Bob Fisher Wed Apr 16 00:58:54 BST 1997

Widefield microscope

Fluorescence microscope

By inserting a microlens array into the optical train of a conventional microscope, one can capture light fields of biological specimens in a single photograph. Although diffraction places a limit on the product of spatial and angular resolution in these light fields, we can nevertheless produce useful perspective views and focal stacks from them. Since microscopes are inherently orthographic devices, perspective views represent a new way to look at microscopic specimens. The ability to create focal stacks from a single photograph allows moving or light-sensitive specimens to be recorded. Applying 3D deconvolution to these focal stacks, we can produce a set of cross sections, which can be visualized using volume rendering. In this paper, we demonstrate a prototype light field microscope (LFM), analyze its optical performance, and show perspective views, focal stacks, and reconstructed volumes for a variety of biological specimens. We also show that synthetic focusing followed by 3D deconvolution is equivalent to applying limited-angle tomography directly to the 4D light field. Information available: The paper (PDF file) 4-minute video (.mov file, MPEG-4, 22 MB) The Powerpoint slides from my presentation at SIGGRAPH 2006. Our project web page, which includes links to more results and movies. LFDisplay: a software package for real-time viewing of microscope light fields. The package includes sample light fields and step-by-step instructions on how to build a Light Field Microscope (LFM). A web page describing other devices we have built to capture light fields. Note: In the printed proceedings, figure 1 came out poorly. Please refer instead to the version in the PDF file (also reproduced above). Optical recipes for light field microscopes non-infinity optics, see memo for caption In our SIGGRAPH paper, figure 2 gives the optical layout of our prototype light field microscope. Unfortunately, this figure and its accompanying caption do not provide quite enough detail to set up and adjust a light field microscope. This brief technical memo provides a more detailed optical layout, with emphasis on how to vertically position and focus each element in the optical train. We show this first for microscopes having non-infinity-corrected optics (as in our SIGGRAPH paper). We then describe an arrangement suitable for microscopes employing infinity-corrected optics, which is the more common case. Finally, we address the often-asked question of whether our microscope light fields contain aliasing. (Yes they do.) infinity optics © Copyright 2006 by Marc Levoy Last update: June 6, 2010 06:34:32 PM

Next: 3x4 Projection Matrix Up: No Title Previous: Overview Imaging Geometry Central Projection Vector notation: where and are 3-vectors, with . Here central projection is represented in the coordinate frame attached to the camera. Generally, there is not direct access to this camera coordinate frame. Instead, we need to determine the mapping from a world coordinate frame to an image coordinate system (see next slide). Bob Fisher Wed Apr 16 00:58:54 BST 1997

Information available: The paper (PDF file) 4-minute video (.mov file, MPEG-4, 22 MB) The Powerpoint slides from my presentation at SIGGRAPH 2006. Our project web page, which includes links to more results and movies. LFDisplay: a software package for real-time viewing of microscope light fields. The package includes sample light fields and step-by-step instructions on how to build a Light Field Microscope (LFM). A web page describing other devices we have built to capture light fields. Note: In the printed proceedings, figure 1 came out poorly. Please refer instead to the version in the PDF file (also reproduced above). Optical recipes for light field microscopes non-infinity optics, see memo for caption In our SIGGRAPH paper, figure 2 gives the optical layout of our prototype light field microscope. Unfortunately, this figure and its accompanying caption do not provide quite enough detail to set up and adjust a light field microscope. This brief technical memo provides a more detailed optical layout, with emphasis on how to vertically position and focus each element in the optical train. We show this first for microscopes having non-infinity-corrected optics (as in our SIGGRAPH paper). We then describe an arrangement suitable for microscopes employing infinity-corrected optics, which is the more common case. Finally, we address the often-asked question of whether our microscope light fields contain aliasing. (Yes they do.) infinity optics © Copyright 2006 by Marc Levoy Last update: June 6, 2010 06:34:32 PM

Stanford University ACM Transactions on Graphics 25(3), Proceedings of SIGGRAPH 2006 Abstract: By inserting a microlens array into the optical train of a conventional microscope, one can capture light fields of biological specimens in a single photograph. Although diffraction places a limit on the product of spatial and angular resolution in these light fields, we can nevertheless produce useful perspective views and focal stacks from them. Since microscopes are inherently orthographic devices, perspective views represent a new way to look at microscopic specimens. The ability to create focal stacks from a single photograph allows moving or light-sensitive specimens to be recorded. Applying 3D deconvolution to these focal stacks, we can produce a set of cross sections, which can be visualized using volume rendering. In this paper, we demonstrate a prototype light field microscope (LFM), analyze its optical performance, and show perspective views, focal stacks, and reconstructed volumes for a variety of biological specimens. We also show that synthetic focusing followed by 3D deconvolution is equivalent to applying limited-angle tomography directly to the 4D light field. Information available: The paper (PDF file) 4-minute video (.mov file, MPEG-4, 22 MB) The Powerpoint slides from my presentation at SIGGRAPH 2006. Our project web page, which includes links to more results and movies. LFDisplay: a software package for real-time viewing of microscope light fields. The package includes sample light fields and step-by-step instructions on how to build a Light Field Microscope (LFM). A web page describing other devices we have built to capture light fields. Note: In the printed proceedings, figure 1 came out poorly. Please refer instead to the version in the PDF file (also reproduced above). Optical recipes for light field microscopes non-infinity optics, see memo for caption In our SIGGRAPH paper, figure 2 gives the optical layout of our prototype light field microscope. Unfortunately, this figure and its accompanying caption do not provide quite enough detail to set up and adjust a light field microscope. This brief technical memo provides a more detailed optical layout, with emphasis on how to vertically position and focus each element in the optical train. We show this first for microscopes having non-infinity-corrected optics (as in our SIGGRAPH paper). We then describe an arrangement suitable for microscopes employing infinity-corrected optics, which is the more common case. Finally, we address the often-asked question of whether our microscope light fields contain aliasing. (Yes they do.) infinity optics © Copyright 2006 by Marc Levoy Last update: June 6, 2010 06:34:32 PM

Lightfield microscopy

Central Projection Vector notation: where and are 3-vectors, with . Here central projection is represented in the coordinate frame attached to the camera. Generally, there is not direct access to this camera coordinate frame. Instead, we need to determine the mapping from a world coordinate frame to an image coordinate system (see next slide). Bob Fisher Wed Apr 16 00:58:54 BST 1997

non-infinity optics, see memo for caption In our SIGGRAPH paper, figure 2 gives the optical layout of our prototype light field microscope. Unfortunately, this figure and its accompanying caption do not provide quite enough detail to set up and adjust a light field microscope. This brief technical memo provides a more detailed optical layout, with emphasis on how to vertically position and focus each element in the optical train. We show this first for microscopes having non-infinity-corrected optics (as in our SIGGRAPH paper). We then describe an arrangement suitable for microscopes employing infinity-corrected optics, which is the more common case. Finally, we address the often-asked question of whether our microscope light fields contain aliasing. (Yes they do.) infinity optics © Copyright 2006 by Marc Levoy Last update: June 6, 2010 06:34:32 PM

Imaging Geometry Central Projection Vector notation: where and are 3-vectors, with . Here central projection is represented in the coordinate frame attached to the camera. Generally, there is not direct access to this camera coordinate frame. Instead, we need to determine the mapping from a world coordinate frame to an image coordinate system (see next slide). Bob Fisher Wed Apr 16 00:58:54 BST 1997

ACM Transactions on Graphics 25(3), Proceedings of SIGGRAPH 2006 Abstract: By inserting a microlens array into the optical train of a conventional microscope, one can capture light fields of biological specimens in a single photograph. Although diffraction places a limit on the product of spatial and angular resolution in these light fields, we can nevertheless produce useful perspective views and focal stacks from them. Since microscopes are inherently orthographic devices, perspective views represent a new way to look at microscopic specimens. The ability to create focal stacks from a single photograph allows moving or light-sensitive specimens to be recorded. Applying 3D deconvolution to these focal stacks, we can produce a set of cross sections, which can be visualized using volume rendering. In this paper, we demonstrate a prototype light field microscope (LFM), analyze its optical performance, and show perspective views, focal stacks, and reconstructed volumes for a variety of biological specimens. We also show that synthetic focusing followed by 3D deconvolution is equivalent to applying limited-angle tomography directly to the 4D light field. Information available: The paper (PDF file) 4-minute video (.mov file, MPEG-4, 22 MB) The Powerpoint slides from my presentation at SIGGRAPH 2006. Our project web page, which includes links to more results and movies. LFDisplay: a software package for real-time viewing of microscope light fields. The package includes sample light fields and step-by-step instructions on how to build a Light Field Microscope (LFM). A web page describing other devices we have built to capture light fields. Note: In the printed proceedings, figure 1 came out poorly. Please refer instead to the version in the PDF file (also reproduced above). Optical recipes for light field microscopes non-infinity optics, see memo for caption In our SIGGRAPH paper, figure 2 gives the optical layout of our prototype light field microscope. Unfortunately, this figure and its accompanying caption do not provide quite enough detail to set up and adjust a light field microscope. This brief technical memo provides a more detailed optical layout, with emphasis on how to vertically position and focus each element in the optical train. We show this first for microscopes having non-infinity-corrected optics (as in our SIGGRAPH paper). We then describe an arrangement suitable for microscopes employing infinity-corrected optics, which is the more common case. Finally, we address the often-asked question of whether our microscope light fields contain aliasing. (Yes they do.) infinity optics © Copyright 2006 by Marc Levoy Last update: June 6, 2010 06:34:32 PM